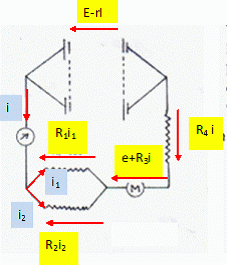
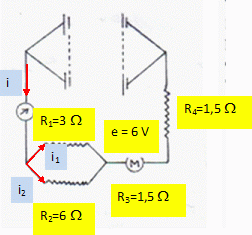
Si le moteur est bloqué, l'intensité vaut i =
2,0 A ; si le moteur fonctionne i = 1,0 A.
Déterminer la fem E
et la résistance interne r du générateur.
R1 et R2 sont équivalentes à Réqui = R1
R2 / (R1+ R2) =3*6 / 9 = 2
ohms.
Additivité des tensions : E-ri = (Réqui + R4) i +
e+R3i = (Réqui + R4+R3) i +
e.
Moteur bloqué : e = 0 ; E-2r = 5*2 = 10.
Le moteur fonctionne : E-r = 5*1 +6 =11.
par suite E = 12 V
et r = 1 ohm.
Quelle
est l'énergie perdue dans R1 par minute si le
moteur travaille ?
W = R1i12 t avec t = 60 s.
Loi des noeuds : i = i1 + i2 = 1 A. De plus : R1i1
= R2i2 ; 3i1 =6i2 ; par
suite i1 = 0,667 A.
W = 3*0,6672*60 = 80 J.
|
Calculer la masse m
de zinc consommée par minute dans le générateur quand le moteur
travaille.
On donne MZn = 66 g/mol et valence n = 2 ; 1 F = 96500 C.
Quantité
d'électricité Q = I t = 1*60 = 60 C
Quantité de matière d'électron n(e-) =Q / F =60 / 96500
=6,22 10-4 mol.
Quantité de matière de zinc : nZn = ½n(e-) =3,11 10-4 mol.
Masse
de zinc : m = nZn
*MZn
=3,11 10-4 *66 =0,0205
~0,021 g.
|
On remplace R2
par R5. Quand le moteur travaille, l'intensité vaut i = 1,2
A.
Calculer
la valeur de R5.
E-ri = (Réqui + R4) i + e+R3i = (Réqui
+ R4+R3) i + e.
Réqui = (E-e) / i -r-R4-R3= (12-6)/1,2
-1-1,5-1,5 = 1 ohm.
Réqui = R1 R5 / (R1+ R5)
; 3+R5 = 3R5 ; R5 = 1,5 W.
On enlève R4 et R5. On monte le moteur en
dérivation avec R1.
Calculer
le
rendement et la puissance du moteur.
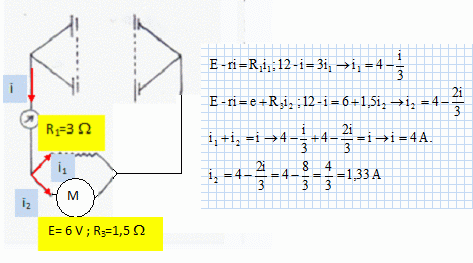
Tension aux bornes du moteur : U = e+R3i2
= 6+1,5*1,33 = 8 V.
Rendement du moteur : h = e
/ u = 6/8 = 0,75.
Puisance mécanique : e i2 = 6*1,33 = 8 W.
On remplace la dérivation par une résistance R6 = 1 ohm.
Comment
grouper les éléments pour avoir une intensité maximale ?
L'intensité est maximale lorsque R6 = r = 1 ohm ( r :
résistance du groupement ).
Si chaque élément a une fem e' = 1,5 V, il faut E/e' = 12/1,5 = 8
éléments en série.
Si la résistance d'un élément est r' =0,5 ohm, la résistance de 8
éléments en série est 8*0,5 =4 ohms.
Pour obtenir r =1 ohm, il faut 4 branches de 8 éléments montées en
dérivation.
Soient 2
électrolyseurs montés en série : le premier contient du nitrate
d'argent, le second du sulfate de cuivre. Au bout de t = 32 min
45 s, il se dépose 6,3 g d'argent à la cathode du premier électolyseur.
MAg = 108 ; MCu = 63,6 g/mol. F = 96500 C.
Quelle est
l'intensité du courant ?
Quantité de matière d'argent nAg = m / MAg =6,3 / 108 = 0,0583
mol.
Or Ag+ +e- = Ag(s); quantité de matière
d'électron n(e-) = n(Ag) = 0,0583 mol.
Quantité de matière d'électricité : Q = n(e-) F =
0,0583*96500 =5629 C
De plus Q = It avec t = 32*60+45 =1965 s, d'où I = 5629 / 1965 =2,86 ~2,9 A.
Calculer la masse de
cuivre déposé sur la cathode de l'autre électrolyseur.
Les électrolyseurs en série sont traversés par la même quantité
d'électricité.
Cu2+ + 2e-
= Cu(s) ; n(Cu) = ½n(e-)=0,0583
/ 2 =0,0292 mol
Masse de cuivre : n(Cu)*MCu
=0,0292*63,6 =1,855~1,9 g.
Un calorimètre
contient 500 g d'eau et 75 g de glace à 0°C.
Quelle est la
quantité de chaleur nécessaire pour faire fondre la glace et porter
toute l'eau à 15°C ?
Chaleur latente de fusion de la glace : 80 kcal kg-1 = 334,4
kJ kg-1.
Capacité thermique massique de l'eau c = 4,18 kJ K-1 kg-1.
On ne tiendra pas compte de la capacité thermique du calorimètre.
Chaleur nécessaire à la fusion de la glace à 0°C ( l'eau de fonte reste
à 0°C ) : 0,075 *334,4 =25,08 kJ.
Chaleur nécessaire pour porter 0,575 kg d'eau de 0°C à 15 °C :
0,575*4,18*15 =36,05 kJ
Soit au total : W =61,13 ~61
kJ.
On réalise cette fusion et cet échauffement en plongeant dans l'eau un
conducteur dont la résistance est 15 ohms et parcouru par un courant de
6 A.
Pendant
combien de temps le courant doit-il passer ?
W = R I2t ; t = W / (RI2) = 61,13 103
/ (15*62) =113 s.
|
Un circuit comprend une pile de 12
éléments identiques, une résistance R et une dérivation de deux
branches : l'une contient un voltamètre ( électrolyseur ) à eau
acidulée et électrodes de platine ; l'autre comprend un petit moteur.
La pile est disposée en trois série de 4 éléments ( e' = 2 V ; r' = 0,3
ohm ).
Calculer
les caractéristiques du groupement.
fem E = 4*2 = 8 V
; r = 4r' / 3 = 4*0,3 / 3 = 0,4 ohm.
La résistance R est un fil de ferro-nickel ( r = 78,5 10-6 W cm ) de 1 m de longueur et 1 mm
de diamètre.
Evaluer
sa résistance.
R = r L/ S avec r = 78,5 10-8 W m ; S = 3,14 * (10-3)2
/ 4 = 7,85 10-7 m2.
R = 78,5 10-8 *1 / 7,85 10-7 = 1 ohm.
Ce fil est plongé dans m= 400 g = 0,40 kg
de pétrole de chaleur massique c =2,1 kJ K-1 kg-1 (
0,5 kcal K-1
kg-1). La température du pétrole s'élève de Dq=1,2°C en t =4 min 10 s ( 250 s ).
Calculer
la tension aux bornes de R.
Energie reçue par le pétrole W = m c Dq = 0,4*2,1*1,2 =1,008 kJ = 1008
J.
D'autre part W = UR I t avec I = UR/R ; W = UR2 t / R ; UR2 = W R / t = 1008 / 250 =
4,032 ; UR = 4,032½=2,0 V.
Calculer
la tension aux bornes du voltamètre.
Additivité des tensions : Ugénérateur = UR
+ Uvoltamètre ; E-ri = UR + Uvoltamètre ;
8-0,4 i = 2,0 + Uvoltamètre ; or i = UR / R = 2,0 / 1 = 2,0 A.
Uvoltamètre = 8-0,4*2-2 =5,2 ~5,2 V.
Le voltamètre a une fcem E' = 1,4 V et de résistance r' = 3,8 ohms.
Calculer
le volume de gaz obtenu à l'anode en 16 min 5 s.
Uvoltamètre =E'+r'i1;
i1 = (Uvoltamètre -E') / r'=
(5,2-1,4) / 3,8 =1,0 A.
Quantité d'électricité : Q = i1 t avec t = 16*60+5 =965 s ;
Q = 1*965 = 965 C.
Quantité de matière d'électrons n(e-) =Q / F = 965 / 96500 =
0,010 mol.
Réaction à l'anode ( oxydation de l'eau) : H2O = ½O2
+ 2H+ +2e- ;
Quantité de matière de dioxygène n(O2) = 0,25 n(e-) = 2,5 10-3
mol.
Volume de dioxygène ( L) = n(O2) fois volume molaire.
Si Vm = 22,4 L /mol alors V = 2,5 10-3 *22,4 = 0,056 L = 56 mL.
La résistance du moteur est 1,2 ohms.
Calculer
la puissance mécanique et le rendement du moteur.
Intensité traversant le moteur : i2 = i-i1 = 2-1
= 1 A.
Tension aux bornes du moteur =Uvoltamètre =5,2 = E'+r'i2
= E' + 1,2*1 d'où la fcem E' du moteur : E' = 4 V.
rendement du moteur : E' / Umoteur = 4 / 5,2 =0,77
Puissance mécanique du moteur : E' i2 =4*1 = 4 W.
|
|