La tension aux bornes d'un condensateur de capacité C = 0,1 µF est U0
= 10 V.
Quelle
est la charge q0 d'une armature
?
q0
= CU0 = 0,1 10-6 * 10 = 1 10-6 C = 1 µC.
Sur le schéma ci-dessous, les électrons se déplacent en sens contraire
du courant : donc durant la première décharge du condensateur qA
<0 et qB >0.
A l'instant t=0 ce condensateur est branché aux bornes d'une bobine de
résistance négligeable et d'inductance L = 1 H. L'intensité du courant
est nulle à cet instant.
Faire le schéma du
montage et établir l'équation différentielle à laquelle obéit la charge
du condensateur.
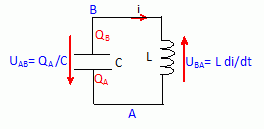
Additivité des tensions : UAB + UBA = 0 ; qA/C
+ Ldi/dt = 0 ;
i = dqA/dt ; di/dt = d2qA/dt2.
par suite : qA/C + Ld2qA/dt2=
0 ; d2qA/dt2+
1/(LC) qA=0.
|
Calculer la
pulsation propre w0 ainsi que la
période propre T0.
w0
=(1/(LC)½ =1/(0,1 10-6)½= 10½ 103
=3,162 103 ~3,2 103 rad s-1.
T0 = 2 p (LC)½ = 2 p (10-7)½
=1,986 10-3 ~ 2,0 10-3 s. |
Montrer par une
étude dimensionnelle que la période a la dimension d'un temps.
énergie magnétique stockée par la bobine Em = ½LI2
; L est une énergie divisée par une intensité au carré : [L]= J A-2.
énergie stockée par le condensateur : E= ½Q2/C ; C est une
charge au carrée divisée par une énergie ; une charge est une intensité
fois un temps
d'où [C] = A2T2 J-1 ; par suite
[LC] =T2 ; [(LC)½] =T ; ajoutons que 2p est sans dimension.
En
utilisant les conditions initiales donner l'expression de la charge
q(t) du condensateur en fonction de t, w0, C et U0
ainsi que l'expression de l'intensité i(t) du courant.
Solution générale de l'équation différentielle : q(t) = A cos(w0t+f)
A t=0, l'armature B porte la charge +q0 d'où : q0
= A cos (f) avec A, amplitude
positive : F=0 et A = q0=
CU0.
qB(t)
= CU0 cos(w0t).
i(t) = dqA/dt = -dqB/dt = -CU0 (-w0) sin(w0t).
i(t) = CU0 (1/LC)½sin(w0t).
i(t) = U0
(C/L)½sin(w0t).
i(t) = 10(10-7)½sin(w0t) = 3,16 10-3 sin(w0t).
En
déduire l'expression de la tension UAB(t) aux bornes du
condensateur.
UAB(t)
= qA/C = - U0 cos(w0t).
UBA(t) = qB/C =
U0
cos(w0t).
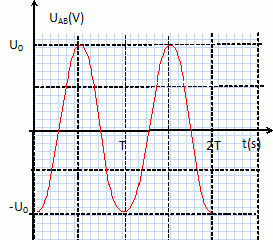
On visualise uAB(t) sur l'écran d'un oscilloscope ( 0,5 ms/div et 5 V /
div).
Représenter
la courbe observée sur l'écran de 8 cm de large.
T = 2 ms ; 8 cm = 8 div = 8*0,5 = 4 ms : on visualise donc 2 périodes.
Donner
l'état du condensateur ( charge, tension aux bornes, énergie stockée)
ainsi que l'intensité du courant et l'énergie WL de la bobine aux
dates t= 0 ; t1 = 0,25 T0 ; t2
= 0,5 T0 ; t3 = 0,75 T0.
date
|
charge
qA(µC)
|
tension
UAB(V)
|
énergie
½CU2AB(µJ) |
intensité
(mA)
|
WL=½Li2
(µJ)
|
0
|
-q0
= -1
|
-U0
= -10
|
5
|
0
|
0
|
| 0,25
T0 |
0
|
0
|
0
|
3,16
|
5
|
|
0,5 T0 |
+q0
= 1 |
U0
= +10 |
5
|
0
|
0
|
| 0,75
T0 |
0
|
0
|
0
|
-3,16
|
5
|
Concours
orthoptie Monpellier 2007.
On charge un condensateur de capacité
C = 2,0 μF sous une tension E constante. Le condensateur est ensuite
branché aux bornes d’un dipôle.
Ce dipôle est successivement :
- une bobine d’inductance L, de résistance négligeable
- une bobine d’inductance L, de résistance r non négligeable,
- un conducteur ohmique de résistance R.
La tension uc aux bornes du condensateur en fonction du
temps obtenue dans chacun cas est représentée sur l’une des figures 1,
2 ou 3.
A quel
dipôle correspond chaque figure ? Justifier votre choix en décrivant le
phénomène observé.
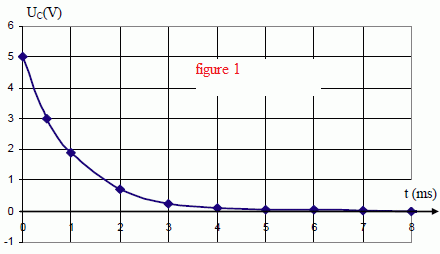
Décharge d'un
condensateur chargé à travers un conducteur ohmique : la tension aux
bornes du condensateur décroît de manière exponentielle jusu'à
s'annuler.
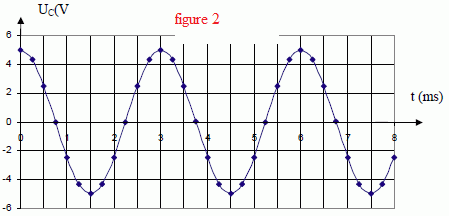
Décharge oscillante du condensateur à travers une bobine de résistance
négligeable : oscillations sinusoïdales.
Il y a échange d'énergie entre bobine et condensateur : l'énergie du
dipôle LC se conserve.
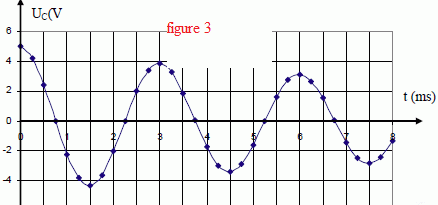
Décharge oscillante du condensateur à travers une bobine de résistance
non négligeable : oscillations amorties ( régime
pseudo-périodique).
Au cours des échanges d'énergie entre bobine et condensateur, une
partie de l'énergie est perdue par effet Joule dans les parties
résistives.
|
A chaque phénomène
observé correspond un temps caractéristique.
Définir
ce temps et le calculer en utilisant le graphique.
En
déduire la valeur de la résistance R du conducteur ohmique, de
l’inductance L de la bobine.
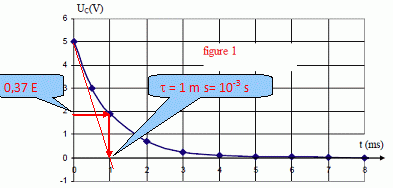
La constante de temps du dipôle RC est égale à : RC = 10-3 s
avec C = 2,0 10-6 F
R = 10-3 /2,0 10-6 =5,0 102 ohms.
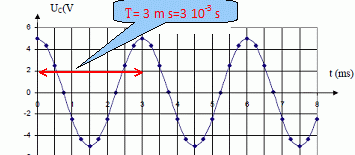
T = 2 p (LC)½ ;
L = T2 / (4 p2C)=9
10-6 /(4*3,142*2 10-6) =0,114 ~0,11 H.
Figure 3 :
la pseudopériode est pratiquement égale à la période T.
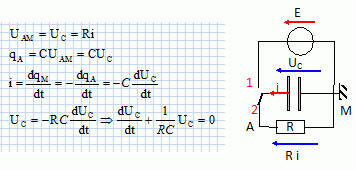
Pour
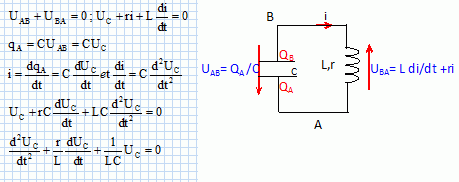
chaque cas faire un schéma du montage constitué du condensateur et du
dipôle étudié. Donner une relation entre les tensions aux bornes des
différents composants contenus dans le circuit.
Etablir
l’équation différentielle à laquelle obéissent les variations de uc en fonction du
temps.
|
Dans le cas où le condensateur se décharge dans une bobine inductive
de résistance négligeable, quelles sont les énergies mises en jeu ? Calculer ces
énergies à t = 0 s ?
Il y a échange d'énergie entre bobine ( énergie magnétique ½Li2) et le condensateur ( énergie électrostatique ½CU2). L'énergie du dipôle se conserve.
A t =0 le condensateur chargé stocke toute l'énergie du dipôle LC.
½CU2= 0,5 * 2 10-6 *52 =2,5 10-5 J.
Dans le cas où le condensateur se décharge dans une bobine inductive
de résistance non négligeable, quelle est l’énergie perdue pendant la première
pseudo-période ? Que
devient cette énergie ?
Au cours des échanges d'énergie entre bobine et condensateur, une
partie de l'énergie est perdue par effet Joule dans les parties
résistives.
La tension aux bornes du condensateur à t = T est égale à 4 V ( lecture graphe figure 3)
½CU2= 0,5 * 2 10-6 *42 =1,6 10-5 J.
Energie dissipée par effet Joule : (2,5-1,6) 10-5 = 9,0 10-6 J.
|








