On négligera toute action de l'air et on prendra g = 9,8 m s-2.
La force exercée par le ressort sur un objet fixé à l'une de ses extrémités, l'autre étant fixe, est une force de rappel F.
Pour un ressort à réponse linéaire F = k |Dl|
- k est le coefficient de raideur du ressort
- Dl désigne l'allongement du ressort : Dl = l-l0 avec l : longueur du ressort et l0 sa longueur à vide.
|
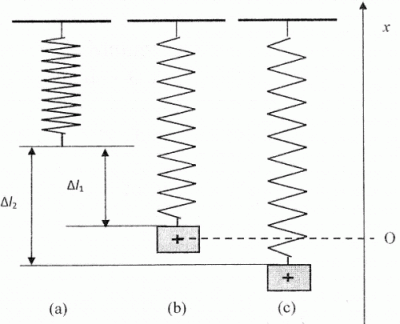
On suspend le ressort verticalement ( schéma (a))
On y accroche un solide S de masse m = 100 g. L'équilibre s'établit pour un allongement Dl1 = 19,6 cm ( schéma (b)).
On tire le solide vers le bas jusqu'à ce que le ressort soit allongé de : Dl2 = 19,6 + 5,0 = 24,6 cm ( schéma (c)).
A l'instant t=0, on lâche le mobile, sans vitesse initiale. On observe
des oscillations du solide de part et d'autre de la position
d'équilibre.
|
k peut s'exprimer en N m-1, mais aussi à l'aide des unités du système international d'unités.
A partir de la realtion F = k |Dl| déterminer les unités de k.
force = masse fois accélération et accélération = longueur divisée par un temps au carré.
[force] = M L T-2 ; [force / allongement] = [k]= M T-2.
k s'exprime en kg s-2.
Recopier le schéma (b) et y ajouter les forces qui s'exercent sur le solide S. En déduire l'expression de k en fonction de m, Dl1 et g.
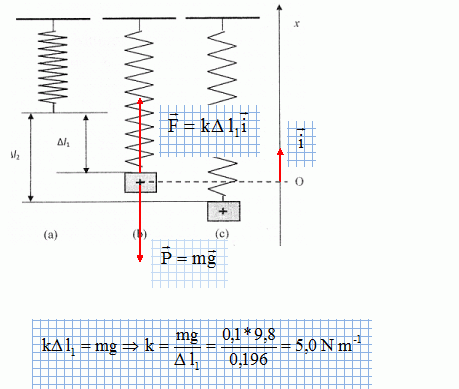
Recopier le schéma (c) et y ajouter les forces qui s'exercent sur le solide S, juste après le lâcher.
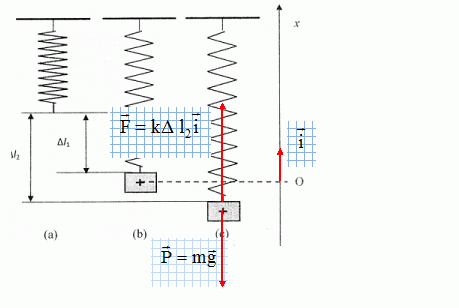
On peut établir que pour t >0, l'abscisse x vérifie l'équation différentielle : m x" + kx = 0.
Montrer que les solutions de cette équation sont de la forme x = A cos (2pt/T0 +f ) et en déduire l'expression de T0 .
x' = -A 2p/T0 sin (2pt/T0 +f ) ; x" = -A [ 2p/T0 ]2 cos (2pt/T0 +f ) ;
repport dans l'équation différentielle : -A m [ 2p/T0 ]2 cos (2pt/T0 +f ) + k Acos (2pt/T0 +f ) = 0
Acos (2pt/T0 +f ) ( -m [ 2p/T0 ]2 +k) = 0.
Cette égalité est vérifiée quel que soit le temps si T0 = 2p ( m / k )½.
Exprimer T0 en fonction de Dl1 et g.
k = mg / Dl1 ; m / k = Dl1 / g ; T0 = 2p ( Dl1 / g )½ = 2p (0,196 / 9,8)½ = 2p *0,14 = 0,89.
|
Quelle
est, parmi les expressions suivantes, celle qui convient ? ( aucune justification n'st demandée )
x(t) = 0,246 cos (2pt / 0,89 ) ; x (t) = 0,246 sin (2pt / 0,89 ) ; x(t) = -0,246 cos (2pt / 0,89 ) ;
x (t) = -0,246 sin (2pt / 0,89 ) ; x (t) = 0,05 cos (2pt / 0,89 ) ; x (t) = 0,05sin (2pt / 0,89 ) ;
x (t) = -0,05 cos (2pt / 0,89 ) ; x (t) = - 0,05sin (2pt / 0,89 ) ;
En utilisant l'expression choisie, exprimer la vitesse du solide en fonction du temps.
Dériver x(t) par rapport au temps :
v(t) = 0,05 *2 p / 0,89 sin (2pt / 0,89 )
v(t) = 0,35 sin (2pt / 0,89 ).
|
|


