Le flash
électronique d’un appareil photo utilise un tube à décharge contenant
de la vapeur de xénon. Le gaz va s’ioniser sous l’action d’une très
haute tension et on pourra obtenir un éclair lumineux. Pour stocker
l’énergie nécessaire E0=10 J, on utilise un condensateur de capacité C
= 400 µF.
Etude du condensateur :
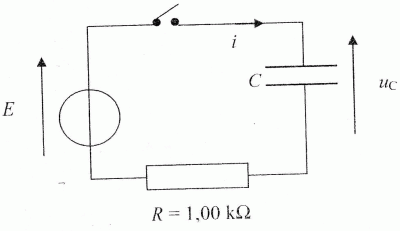
Pour vérifier la valeur de la capacité du condensateur, on réalise le
circuit suivant utilisant un générateur de force électromotrice E1 =
3,0 V et une résistance R = 1,00 kiloohm. A un instant de date t=0, on
ferme le circuit.
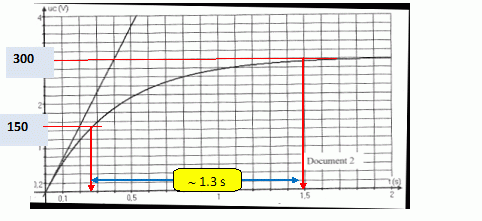
Un dispositif d’acquisition non représenté permet d’obtenir la courbe
suivante donnant la tension uC en fonction du temps lorsqu’on charge le
condensateur. La tangente à l’origine est également tracée.
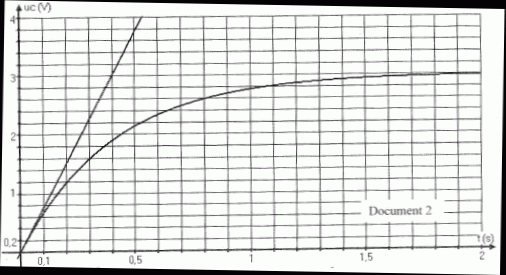Document 2.
On appelle uR la tension aux bornes de la résistance.
Donner la relation entre uR et i puis entre i et uC.
uR = R i ; q = C uC et i = dq/dt = CduC/dt.
Quelle relation y a-t-il entre E1, uR et uC ?
Additivité des tensions : E1 = uR + uC.
Etablir l’équation différentielle vérifiée par uC.
E1 = R i + uC ; E1 = RCduC/dt + uC (1).
|
Montrer que la fonction uC = E1(1-exp(-t/t)) est solution de l’équation
différentielle et déduire l’expression de t en fonction de R et C.
duC/dt = E1 / t exp(-t/t)
repport dans (1) :
E1 = RC E1 / t exp(-t/t)+ E1- E1exp(-t/t).
Cette égalité est vérifiée quel que soit le temps si : t = RC.
|
Par lecture graphique, déterminer la valeur de t. Déduire la valeur de
C. Cette valeur est-elle en accord avec les données ?
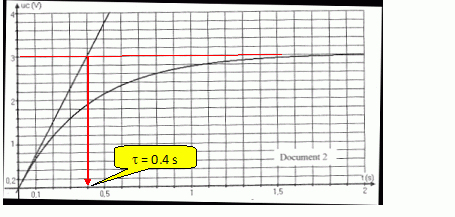
C = t / R =0,4 / 1000 = 4 10-4 F = 4 102 µF. ( accord avec la valeur donnée)
Calculer l’énergie E emmagasinée par le condensateur lorsque celui-ci
est chargé. Cette énergie est-elle suffisante pour faire fonctionner le
flash ?
E = ½CE12 = 0,5 *4 10-4 * 32 =1,8 10-3 J.
Cette valeur est bien inférieure à 10 J ; le flash ne fonctionne pas.
Condensateur
et tube à décharge :
Dans le circuit électronique de l’appareil photo, un dispositif
élévateur de tension permet de charger le condensateur sous une tension
E2 = 300 V à travers une résistance R = 1,00 kW. En ce qui concerne la
charge du condensateur, le montage peut être schématisé comme dans
l’étude précédente.
La valeur de t est-elle modifiée ? Que faudrait-il modifier sur le document 2 pour que la
courbe représente la variation de uC lors de la charge du
condensateur ?
La constante de temps ne dépend que de R et C : elle n'est donc pas modifiée.
Il faudrait modifier l'échelle sur l'axe vertical ( remplacer 3,0 par 300 V ).
Calculer l’énergie E emmagasinée par le condensateur lorsque celui-ci
est chargé. Cette énergie est-elle suffisante pour faire fonctionner le
flash ?
E = ½CE22 = 0,5 *4 10-4 * 3002 =18 J.
Cette valeur est supérieure à 10 J ; le flash fonctionne.
Lorsque le condensateur se décharge à travers le tube à décharge, le
circuit peut être modélisé ainsi :
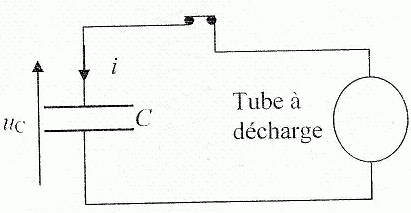
Toute l’énergie fournie par le condensateur est utilisée dans le tube.
La tension aux bornes du condensateur diminue à partir de 300 V.
Quel est le signe de i ? Justifier.
Lors
de la décharge complète les armatures du condensateur redeviennent
identiques. Les électrons se déplacent en sens contraire par rapport à
la charge.
L'intensité du courant de décharge est de sens contraire au courant de charge.
|
Un dispositif électronique permet de stopper la décharge lorsque la tension aux bornes du condensateur vaut 150 V.
Quelle est l’énergie encore emmagasinée dans le condensateur ? Quelle
est l’énergie reçue par le tube ?
Energie encore stockée dans le condensateur : ½*4 10-4 * 1502 = 4,5 J.
Energie reçue par le tube : 18-4,5 = 13,5 J.
Déterminer la durée nécessaire à la charge pour que la tension aux
bornes du condensateur passe de la valeur 150 V à 295 V ? Expliquer
votre démarche.
|