On
souhaite étudier le mouvement d'une balle dans un champ de pesanteur
uniforme. On relève les coordonnées du centre d'inertie de cette balle
dans un repère (O, i, k ) défini par un axe Ox horizontal et un axe Oz
vertical ascendant.
La date t=0 est choisie sur la première image. Les valeurs (x, z et t
sont traitées par un logiciel adapté qui donne les graphes suivants :
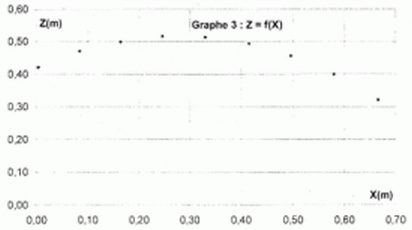
Quel graphe représente la trajectoire de la balle ? Justifier.
On doit avoir l'altitude z en ordonnée et x sur l'axe horizontal : z = f(x). Le graphe n° 3 correspond.
Justifier
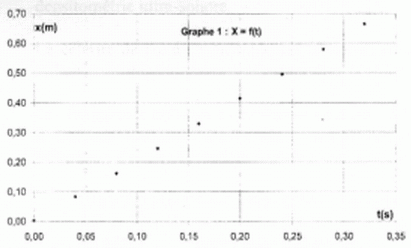
la nature du mouvement sur Ox en précisant le graphe utilisé. En
déduire la valeur de la vitesse vx selon l'axe Ox et l'équation horaire
x(t).
La chute est libre : l'accélération est verticale descendante de valeur g = 9,8 m s-2.
La composante de l'accélération est nulle suivant Ox ; sur cet axe, le mouvement est rectiligne uniforme.
Le coefficient directeur de la droite du graphe n°1 donne la valeur Vx.
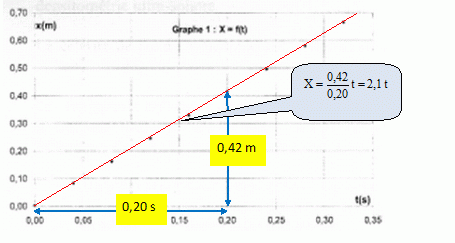
Vx = 2,1 m/s.
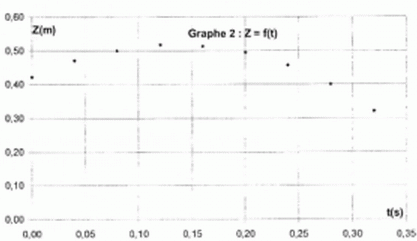
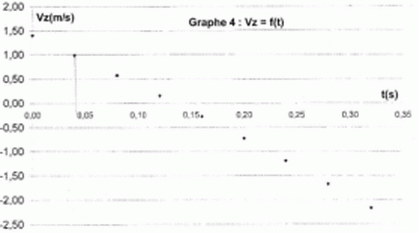
A l'aide du graphe 4, déterminer l'équation horaireVz(t). Donner la signification et l'unité de chaque constante. En déduire l'équation horaire du graphe 2.
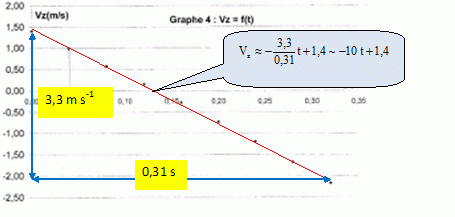
10 ms-2, accélération ; 1,4 m s-1 : valeur de la vitesse initiale suivant Oz.
z(t) est une primitive de vz(t) : z(t) = -5 t2 +1,4t+ cste. Le graphe 2 donne la valeur de l'altitude initiale : 0,42 m.
z(t) = -5 t2 +1,4t + 0,42.
Déterminer l'équation horaire de la trajectoire.
x = 2,1 t soit t = x/2,1.
Repport dans z(t) : z(x) =-5x2/2,12 +1,4 x/2,1 +0,42.
z(x) = -1,1 x2 + 0,67 x +0,42.
|
Quels sont l'angle initial et la vitesse initiale sous lesquels la balle est lancée ?
z(x) = -1,13 x2 + 0,67 x +0,42.
z(x) = -½gx2 /(v0cosa)2 +tan a x + 0,42.
par identification : tan a =0,67 ; a = 34°.
1,13 = ½g/(v0cosa)2 ; 0,47 = 1/(v0cosa) ; v0 = 1/(0,47 *cos34) = 2,5 m/s.
Déterminer la date tS et les coordonnées( xS ; zS ) de la balle lorsque celle-ci touche le sol.
zS = -1,13 xS2 + 0,67 xS +0,42 =0 ;
D = 0,672 +4*1,13*0,42 =2,35 ; D½ =1,53.
xS =(-0,67 -1,53) / (-2*1,13) = 0,97 m.
xS = 2,1 tS ; tS =xS / 2,1 =0,97 / 2,1 =0,46 s.
|
|