Bille
sur une sphère.
Une
bille de masse m quitte la position initiale en B sans vitesse. Elle
glisse sans frottement sur la sphère. Elle quitte la sphère en une
position q
égale à : 30°, 45°, 48°, 90°.
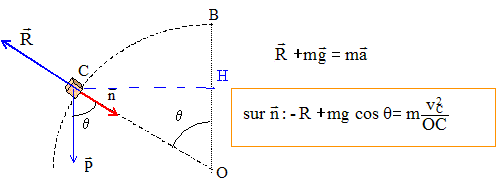
Théorème de
l'énergie cinétique entre B et C :
L'action du sol, perpendiculaire à la vitesse, ne travaille pas.
travail moteur du poids : mgBH = mgOB(1-cos q)
½mv2C-0 =mgOB(1-cos q) ; ½v2C-0
=gOB(1-cos q) ; v2C
= 2gOB(1-cos q) (2)
Question relative à l'angle q à l'instant du décollage.
A cet instant l'action du plan
est nulle : R=0 ; v2C
=g OCcos q. (1)
avec
OB=OC= r.
g r cos q
= 2g r (1-cos q) ; cos q = 2 (1-cos q) ; cos
q =2/3; q
= 48°.
Bille
dans un fluide.
Une
bille se déplaçant dans un fluide subit une force de frottement F qui
dépend de la vitesse V de la bille , de son rayon r et de la viscosité h du fluide ( en
kg m-1 s-1). Soit K une
constante sans dimension.
Une expression possible de la valeur de F est :
KV/(rh) ;
K/(rhV) ;
Krh/V ; KrhV.
Une force est une masse fois une accélération soit une masse fois une
longueur divisée par le carré d'un temps : [F] = M L T-2
( kg m s-2)
(rh)
s'exprime en kg s-1 ; V
s'exprime en m s-1 ; V/(rh) s'exprime en :
m kg-1 ; ne
convient pas.
(rhV)
s'exprime en kg m s-2 et 1 /(rhV) en kg-1s2
m-1: ne convient pas.
rh/V
s'exprime en kg m-1 : ne convient pas.
RhV
s'exprime en kg m s-2 :
convient.
|
Saut
à l'élastique.
Un
sportif de masse m = 85 kg se jette d'un pont en O sans vitesse
initiale. Ses pieds sont attachés à un élastique, lui même fixé au
parapet du pont. Le mouvement du sauteur est une translation verticale.
La chute libre s'effectue pendant 25 m jusqu'au point E. En ce point
l'élastique commence à se tendre et à exercer une force verticale F,
qui ne dépend que de l'allongement de l'élastique. Le sportif chute
encore de 60 m jusqu'en B tel que EB = 60 m, où il
s'immobilise
une fraction de seconde, puis remonte.On donne g = 10 m s-2.
Le travail ( en kJ) de la force F au cours du déplacement E à B est
égale à : 8,5 ; -51 ; -72 ; 51
Ecrire le théorème de l'énergie cinétique entre le point O et le point
B.
La variation de l'énergie cinétique
est nulle: vitesses initiale et finale nulles.
Travail moteur du poids en descente : mg OB = 85*10*85 =7,2 104
J = 72 kJ.
Travail de F : W ; la somme des travaux des forces est égale
à la variation de l'énergie cinétique.
W = 72 = 0 ; W = -72 kJ.
|
Sarbacane.
Une
sarbacane cylindrique de longueur L = 1,0 m, en position horizontale,
est utilisée pour lancer des fléchettes de masse 10 g. Le souffleur
exerce une force constante F, paralèlle à l'axe de la sarbacane. Une
fois sortie de la sarbacane la flèche est soumise de la part de l'air à
une force de frottement de valeur f = k V avec V la vitesse et k = 5 10-3
kg s-1.
On néglige le poids de la flèche devant F et tout frottement dans la
sarbacane. La vitesse initiale des flèches est nulle. On prendra t = 0
à la sortie de la sarbacane.
A- La
vitesse de la flèche à la sortie de la sarbacane s'écrit V0
= [2LF/ m]½.
Vrai.
Ecrire le théorème de l'énergie cinétique entre le départ et la sortie
de la sarbacane.
½mV02-0 = FL ; V02=
2 F L / m.
B- La
vitesse de la flèche à la sortie de la sarbacane s'écrit V0
= [LF/ m]½. Faux.
C- La
vitesse de la flèche une fois sortie de la sarbacane s'écrit V(t) = V0
exp(-k/m t). Faux.
Dans l'hypothèse où le poids est négligé : écrire la seconde loi de Newton sur un axe horizontal : -kv = m dv/dt ;
dv/dt +k/m v = 0
La solution générale de cette équation différentielle est : v(t) = A
exp(-k/m t) avec A une constante.
A t=0, v(0) = V0 = A d'où v(t) = V0
exp (-k/m t).
Or le texte n'indique pas que le poids est négligé à la sortie de la sarbacane.
D-
La vitesse de la flèche une fois sortie de la sarbacane s'écrit V(t) = V0
exp(+k/m t). Faux.
Chute
avec frottement.
Une petite brindille de masse m = 4,0 g tombe sans vitesse initiale
d'une hauteur h = 8,0 m. Pendant sa chute, elle est soumise à une
action résistante due à l'air de valeur F = 24 mN. Prendre g = 10 SI.
A- la brindille est
en chute libre. Faux.
Un corps en chute libre n'est soumis qu'à son poids.
B- Sa vitesse à son
arrivée au sol est 8 m/s. Vrai.
Ecrire le théorème de l'énergie cinétique entre le départ et l'arrivée
au sol : DEc
= ½mv2-0 = mgh -F h
v2= 2gh-2Fh/m =
20*8 -0,048*8/0,004 =160-96=64 ; v =8 m/s.
C- Son
accélération est égale à 4,0 m s-2. Vrai.
Ecrire la seconde loi de newton sur un axe vertical descendant : mg -F
= ma ; a = g-F/m = 10 - 24/4 = 4,0 m s-2.
D- La durée de la
chute de la brindille vaut t = 2,0 s. Vrai.
h = ½at2 ; t = [2h/a]½
=(2*8/4)½ =2,0 s.
Un oscillateur est constitué par une masse ponctuelle m
= 0,2 kg acrochée à un ressort de raideur k = 5 N m-1.
La masse oscille sans frottement suivant un axe horizontal sur lequel
la masse est repérée par son abscisse x. Lorsque le ressort est au
repos x=0. A t=0, la masse est située en x=0 et est animée de la
vitesse v = 0,6 m/s vers les x négatifs.
L'équation horaire du mouvement est ( x en mètre) : x = 0,12 sin(5t) ;
x = -12 sin (5t) ; x = -0,6 sin(5t) ; x = -0,12 sin(5t) ; x = 0,12 cos (5t+½p).
x= A cos(wt+j) ; w= (k/m)½
=(5/0,2)½ =5 rad/s.
A t=0 : 0 = A cos j
; A amplitude non nulle ; j
=½p.
Vitesse : v = dx/dt = -A*5 sin(wt+j) ; v(0) = -0,6 =
-5A ; A = 0,6/5 = 0,12 m.
Satellite.
Un satellite de masse m gravite autour de la terre ( supposée homogène
) spghérique de centre O, de rayon R et de masse M sur une orbite
circulaire de centre O et de rayon r.
L'énergie potentielle du satellite est : Ep = -GMm / r.
A-
L'accélération du satellite est normale et centrifuge. Faux.
Dans
le référentiel géocentrique, le satellite n'est soumis qu' à la force
de gravitation de la terre, centripète, dirigée vers le centre de la
terre.
B-
L'énergie cinétique du satellite est donnée par l'expression : Ec =
GMm/r. Faux.
Vitesse du satellite sur son orbite : v2
= GM/r ; Ec = ½mv2 = ½GMm/r.
C-
l'énergie mécanique du satellite est nulle. Faux.
EM= Ep+Ec =
-GMm/r + ½GMm/r = -½GMm/r.
D-
l'énergie mécanique du satellite est -½GMm/r.Vrai.
Electromagnétisme.
Un
condensateur de capacité C, préalablement chargé sous une tension U,
est relié à une bobine d'inductance L et de résistance négligeable. Un
oscilloscope à mémoire est relié aux bornes du condensateur et permet
d'observer environ deux périodes de l'oscillateur. L= 0,10 H ; C = 10
µF.
A- On
peut visualiser directement l'intensité du courant avec cet
oscilloscope.
Faux.
On
peut demander le calcul de la dérivée dU/dt, puis le calcul C du/dt =
dq/dt = i et faire tracer la courbe i(t) = f(t).
B- La
période des oscillations est T = 6,3 ms. Vrai.
T
= 2pi (LC)½ = 6,28 (0,1 * 10-5)
= 6,28 10-3 s = 6,28 ms.
C- La
valeur maximale de l'intensité est Imax = U(C/L)½.
Vrai.
Energie
maximale stockée par le condensateur ½CU2 ;
énergie maximale stockée par la bobine : ½LI2max.
Conservation de l'énergie en l'absence de résistance : ½CU2
=
½LI2max ; Imax
= U(C/L)½.
D-
L'énergie dans la bobine est périodique de période T. Faux.
L'énergie stockée par la bobine est proportionnelle au carré de
l'intensité, soit à sin2(wt) ; la
période de sin2(wt) est égale à la
moitié de la période de sin(wt).
Les
deux lampes L1 et L2 sont
identiques. les deux bobines ont une résistance négligeable et L = 2 L'.
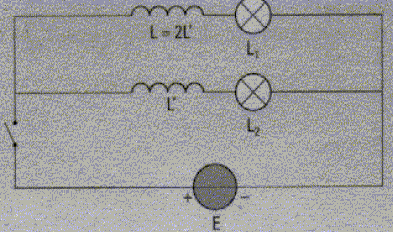
A- A
la fermeture de l'interrupteur, les deux lampes s'allument
simultanément, mais la lampe L1 brille plus que
la lampe L2. Faux.
B- A
la fermeture de l'interrupteur, la lampe L1
s'allume après la lampe L2.
Vrai.
Le retard à l'allumage est d'autant plus grand que l'inductance est
plus élevée.
C-
Lorsque le régime permanent est atteint, après fermeture de
l'interrupteur, la tension aux bornes de L1 est
supérieure à la tension aux bornes de L2, donc
la lampe L1 brille plus que L2. Faux.
En régime permanent, la tension aux bornes des bobines inductives est
nulle ; la tension aux bornes de chaque lampe est égale à E.
D-
Lorsque le régime permanent est établi, la bobine d'inductance L a
emmagasiné la plus grande énergie.
Vrai.
En régime permanent, l''intensité est la même dans chaque branche ; de
plus l'énergie stockée par une bobine est ½LI2 ;
la bobine ayant la plus grande inductance stocke le plus d'énergie.
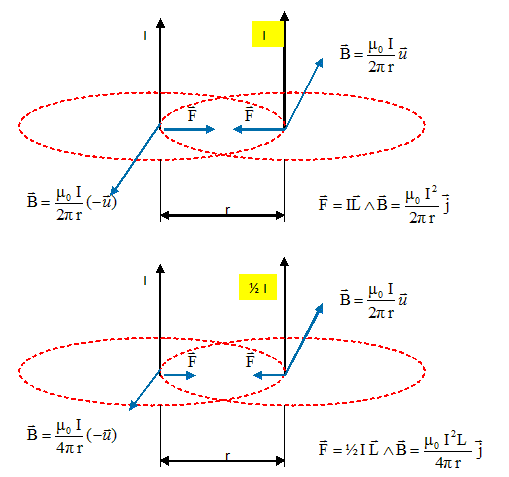
Force
de Laplace.
Deux fils conducteurs parallèles de même longueur sont parcourus par
une intensité électrique I dans le même sens.
On diminue de moitié l'intensité dans l'un des deux fils. la force de
Laplace exercée par un fil sur l'autre :
A- est divisée par
2. Vrai.
B-
est multipliée par 2.
Faux.
C- est
divisée par 4.
Faux.
D- ne
change pas.
Faux.
|
 . .
|


 .
.