Bobine
inductive
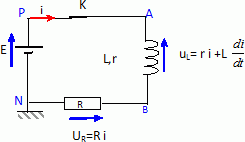
Pour étudier l'établissement du courant dans un
solénoïde( bobine d'inductance L, de résistance r ), on réalise le
circuit suivant.
A l'aide
d'un système d'acquisition de mesures, on mesure la tension uR(t) que l'on
schématisera sur le schéma ( R = 20 ohms).
Comment
peut-on avoir accès à l'intensité du courant i(t) ?
uR(t) = R i(t) = 20 i(t).
L'image de l'intensité i(t) est l'image de la tension uR(t)
divisée par R=20 ohms.
Lorsque
le régime permanent est atteint, l'intensité du courant I a pour
valeur 0,12 A.
En déduire la valeur
de la résistance totale RT du circuit. On donne E = 4,0 V.
En régime permanent, l'additivité des tensions
donne : E = RI + rI = (R+r)I = RT I.
RT = E/I = 4,0 / 0,12 =33,3 ~33 ohms.
A partir
de la courbe i=f(t), déterminer la durée au bout de laquelle
l'intensité atteint 63 % de sa valeur maximale. En déduire la constante
de temps t du circuit.
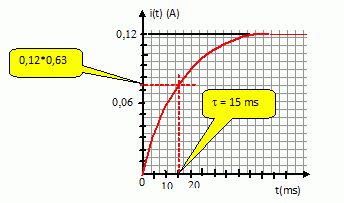
L'expression de la constante de temps du circuit est t = L/RT.
Vérifier
que la valeur de l'inductance est L=0,5 H.
L = t RT =
0,015*33,3~0,5 H.
|
Exprimer l'énergie
magnétique emmagasinnée dans la bobine en régime permanent. Quelle est
sa valeur ?
Emag = ½LI2 = 0,5*0,5*0,122 =3,6 10-3
J.
Exprimer
la puissance joule mise en jeu dans la bobine en régime permanent.
Quelle est sa valeur ?
PJ = r I2 avec r = 33,3-20 = 13,3 ohms.
PJ =13,3*0,122
=0,19W. |
Seconde partie.
l'exploration médicale par l'IrM utilise des champs magnétiques
intenses de l'ordre de 1 T. La valeur du champ magnétique s'exprime par
B = 4 p 10-7 n I,
n étant le nombre de spires par mètre et I l'intensité..
Quel
serait le nombre de spires par mètre de longueur du solénoïde pour
obtenir un champ magnétique de 1 T si I = 0,12 A ? Est-ce réalisable ?
n
= B / ( 4 p 10-7
I) = 1/( 4 *3,14 10-7
*0,12)=6,6 106. C'est irréalisable.
La bobine utilisée a
un nombre de spires par mètre de longueur de 13500.
Quelle
est l'intensité du courant si B = 1 T ?
I=
B / ( 4 p 10-7
n) = 1/( 4 *3,14 10-7
*13500)=6,6 106~59 A.
Radioactivité.
Le phosphore 32 3215P est un isotope radioactif du phosphore, émetteur ß-,
de demi-vie T = 14 jours. Il est utilisé dans le traitement de
certaines pathologies du sang ; la dose thérapeutique est de 4,0 108 Bq par kilogramme de masse corporelle, à 10 % près.
Il existe trois type de désintégrations radioactives a, ß-et ß+.
Quelle est la nature des particules émises dans chacune de ces désintégrations ?
a : noyau d'hélium ; ß- : électron ; ß+ : positon.
Ecrire
l'équation de la désintégration du phosphore 32 en précisant les règles utilisées.
3215P --> AZX + 0-1e.
Conservation de la charge : 15 = Z -1 ; d'où Z = 16. ( élément soufre)
3215P --> 3216S + 0-1e.
Conservation du nombre de nucléons : 32 = A.
Déterminer la valeur de la constante radioactive.
l = ln 2 / T = ln2 / 14 = 4,95 10-2 jour-1.
On a préparé à un jour donné J0 une capsule radioactive d'activité A0 = 3,5 1010 Bq qui par suite d'un contre temps n'a pas été utilisée.
Calculer son activité A au bout de 10 jours( J10). Peut-elle encore être utilisée à J10 pour traiter une patiente de 58 kg ?
A= A0 exp(-l t) = 3,5 1010 exp( -4,95 10-2 *10) = 2,1 1010 Bq.
La dose thérapeutique est de 4,0 108 Bq par kilogramme de masse corporelle, à 10 % près.
4,0 108 *58 =2,3 1010 Bq.
On peut encore traiter la patiente : (2,3 1010 -2,1 1010 ) / (2,2 1010) *100~9 %.
|
Partie 2.
Le phosphore 30 3015P est un isotope radioactif du phosphore, émetteur ß+,
de demi-vie T = 15 heures.
Ecrire
l'équation de la désintégration du phosphore 32 en précisant les règles utilisées.
3015P --> AZX + 01e.
Conservation de la charge : 15 = Z +1 ; d'où Z = 14. ( élément silicium )
3015P --> 3014Si + 01e.
Conservation du nombre de nucléons : 30 = A.
On injecte dans le sang d'un individu 10 mL d'une solution contenant initialement du phosphore 30 à la concentration de 1,0 10-3 mol/L. On prélève au bout de 6 heures, 10 mL de sang du même individu on trouve alors 1,5 10-8 mol de phosphore 30.
En supposant que le phosphore 30 est réparti uniformément, calculer le volume sanguin de l'individu.
NA = 6,02 1023 mol-1.
l = ln2 / 15 = 4,62 10-2 heure-1.
N0 = 0,010*1,0 10-3 * 6,02 1023 = 6,02 1018 atomes de phosphore 30.
N = N0 exp(-l t) =6,02 1018 exp(-4,62 10-2 *6) =4,56 1018 atomes de phosphore 30.
Quantité de matière correspondante : n= 4,56 1018 / 6,02 1023 =7,58 10-6 mol dans tout le volume sanguin..
Concentration C = n / V avec V : volume sanguin.
7,58 10-6 / V = 1,5 10-8 /0,010 =1,5 10-6 ; V = 7,58 10-6 /1,5 10-6 = 5,1 L.
|
|

