On
se propose de reprendre les principales étapes qui ont conduit le
physicien Bohr à établir la quantification de l'énergie de l'atome
d'hydrogène. Dans son étude, Bohr a quantifié le moment cinétique
orbital de l'électron se. Ce paramètre s'écrit : se= r m v
avec r, rayon de l'orbite circulaire de l'électron, m, sa masse et v sa vitesse linéaire.
La quantification s'écrit : se= nh/(2p), avec n entier positif et h la constante de Plank.
Dans l'atome d'hydrogène H, le proton p(noyau) a une masse beaucoupe
plus grande que celle de l'électron, ce qui nous permet de considérer
que le noyau est fixe. Le référentiel, avec le noyau pour origine est
galiléen.
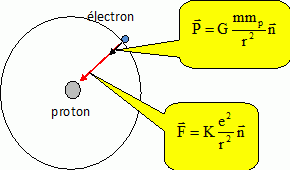
Nommer et exprimer les normes des forces qui s'exercent sur l'électron ; faire un schéma.
La force attractive de gravitation P= G mP m / r2.
La force attractive de Coulomb entre charges de signe contraire. F = 9 109 e2/r2 = Ke2/r2 .
Exprimer le rapport des modules des forces ( ce rapport sera choisi supérieur à 1).
F / P = Ke2 / (G mmp) = 9 109 *(1,6 10-19)2 / (6,67 10-11*9 10-31*1,6 10-27) =2,4 1039.
Rappeler et expliciter brièvement les trois lois de Newton de la physique classique.
|
1ère
loi de Newton
Un référentiel
galiléen est un référentiel dans lequel
le principe de l’inertie est
vérifié.
Dans
un référentiel galiléen, si la somme
vectorielle des forces extérieures appliquées
à un solide est nulle ( solide pseudo-isolé )
alors le centre d’inertie G de ce solide est soit au
repos, soit animé d'un mouvement rectiligne uniforme
et réciproquement.
Un solide peut donc se
déplacer même si la somme des forces
appliquées à ce solide soit nulle. La
véritable opposition n'est pas entre mouvement et
repos mais entre mouvement rectiligne uniforme (le repos
n'est qu'un simple cas particulier) et les autres types de
mouvement..
|
2ème
loi de Newton
Dans un
référentiel galiléen, si le vecteur
vitesse du centre d'inertie d'un solide varie, alors la
somme vectorielle des forces extérieures
appliquées à ce solide n'est pas nulle et
réciproquement. La direction et le sens de cette
somme sont ceux de la variation du vecteur vitesse entre
deux instants proches.
Dans
un référentiel galiléen, la somme
vectorielle des forces extérieures appliquées
à un solide est égale au produit de la masse M
du solide par l'accélération de son centre
d'inertie.
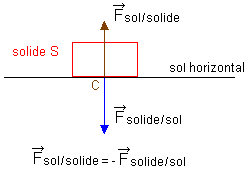
3ème
loi de Newton
Interaction entre un objet A
et un objet B : si un solide noté A exerce sur un
solide noté B une force notée F A /
B, alors B exerce sur A une force notée F
B / A . Les deux forces associées à une
même interaction sont toujours égales et
opposées.
A partir d'une des lois précédentes, montrer que le mouvement de l'électron est uniforme ; faire un schéma.
La force de gravitation est négligeable devant la force de Coulomb ;
celle-ci est constamment perpendiculaire à la vitesse et en conséquence
elle ne travaille pas.
D'après le théorème de l'énergie cinétique, l'énergie cinétique et donc la norme de la vitesse, restent constante.
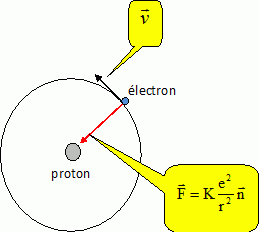
Le mouvement de l'électron est un mouvement dit à force centrale : la
force de Coulomb est constamment dirigée vers le noyau de l'atome
d'hydrogène.
La seconde loi de Newton conduit à : a = K e2 / (mr2) = v2/r = constante.
Exprimer la vitesse v = f(r).
K e2 / (mr2) = v2/r ; K e2 / (mr) = v2 ; v = e (K/mr)½.
Exprimer l'énergie totale de l'atome sachant que l'énergie potentielle est Ep = -Ke2/r.
l'énergie est la somme de l'énergie cinétique et de l'énergie potentielle :
E = ½mv2 - Ke2/r avec mv2 = Ke2/r
E = ½Ke2/r- Ke2/r = -½Ke2/r.
A l'aide de la quantification de se, établir l'expression de r, notamment en fonction de la permittivité e0. On rappelle que K = 1/(4pe0).
se= r m v ; or v = e (K/mr)½.
se= r meK½ / (mr)½ = (mr)½eK½
La quantification s'écrit : se= nh/(2p), avec n entier positif.
nh/(2p) = (mr)½eK½
Elever au carré : n2h2/(4p2) =mre2K
r =4pe0 n2h2/(4m p2e2) = e0 n2h2/(m pe2).
On appelle rayon de Bohr la longueur a0 =e0 h2/(m pe2).
Exprimer l'énergie totale de l'atome en fonction de a0 et conclure.
r = a0 n2. E = -½Ke2/r =-½Ke2/(a0 n2) =-½Ke2/(a0 ) * 1/n2 = -E0/n2.
L'énergie de l'atome est quantifiée.
Au vu de cette étude, quel domaine de la physique classique a certainement inspiré Bohr au cours de ces travaux ?
Dans le référentiel héliocentrique, les planètes décrivent des trajectoires à peu près circulaires centrées sur le Soleil.


