QCM
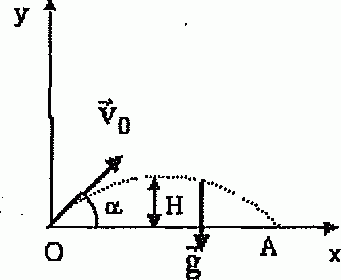
Un ballon de football est lancé d'un point O, à
la date t=0. La direction du vecteur vitesse initiale v0 de
son centre d'inertie fait un angle a
avec l'horizontale. On suppose que la résistance de l'air sur le ballon
est négligeable. Le référentiel terrestre, dans lequel le mouvement est
étudié, est supposé galiléen.
Pour
décrire le mouvement de G, on peut le décomposer en deux mouvements
rectilignes, l'un suivant l'axe horizontal Ox, l'autre suivant l'axe
vertical Oy. Les coordonnées de son vecteur vitesse seront notées vx
et vy, celles de son vecteur accélération ax et ay.
Les coordonnées du
vecteur accélération sont :
ax=0 ; ay=
g ; ay = -g ; ay
= vyt.
Le mouvement de G
suivant l'axe Ox est :
rectiligne uniformément accéléré ; rectiligne uniforme
; rectiligne uniformément retardé ; parabolique.
La courbe
représentant vy = f(t) est celle :
d'une
fonction affine ; d'une hyperbole ; d'une fonction racine carrée
; d'une parabole..
vy
= -gt + v0 sin a.
Au sommet de la
trajectoire, la vitesse vaut :
v0 ; v0
cos a
; vx sin a ; v0
tan a.
La composante verticale de la
vitesse est nulle.
La portée xA
=v02 sin(2a)
/ g.
- augmente quand la valeur de la vitesse
initiale diminue, a étant
fixé. Faux.
- est indépendante de la valeur de la vitesse initiale si a est fixé. Faux.
- est maximale pour a = 45°
pour une même vitesse initiale v0. Vrai.
La valeur de sin (2a) vaut sin 90 = 1.
- est identique pour deux angles a
particuliers, v0 étant fixée. Vrai.
sin(2a) = xAg/v20 ( il existe un angle ß tel
que sin ß =xAg/v20
si xAg/v20
inférieur ou égal à 1 )
d'où 2a = ß ; a = ½ß et 2a = p-ß ; a = ½p-½ß.
|
La flèche yH = v02 sin2a (2g) est
:
- d'autant plus grande que la vitesse initiale est grande.
il faudrait préciser pour une même angle a
-
d'autant plus grande que l'angle de lancement a est grand
il faudrait préciser pour
une même vitesse initiale
- maximale si a=45°, pour
une même vitesse initiale
la valeur du sinus est
maximale pour a = 90°.
- maximale si a = 90°, pour
une même vitesse initiale. Vrai.
|
Electricité.
Un condensateur de capacité C= 1,0 µF est chargé sous une tension E
constante.
Première partie :
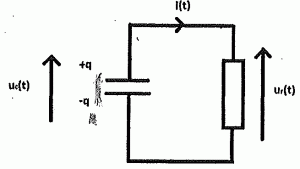
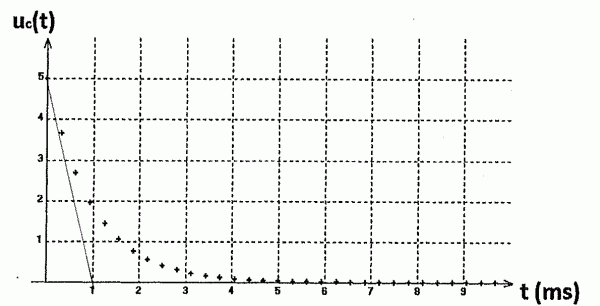
Lorsque le condensateur est chargé,
il est branché aux bornes d'un conducteur ohmique de résistance r. le
graphique donnant la tension uC(t) aux bornes du condensateur est donné
ci-dessous:
Quelle
est l'expression littérale de la constante de temps ?
t = r C.
Déterminer
graphiquement sa valeur.
Intersection de la tangent à l'origine avec l'asymptote horizontale. t = 1 ms = 10-3 s.
En
déduire la valeur de la résistance r.
rC = 10-3 ; 10-6 r = 10-3 ; r = 1000
ohms.
Préciser
la realtion entre uC et ur.
uC = ur.
En
déduire l'équation différentielle à laquelle obéit uc(t).
ur = r i(t) avec i(t) = - dq/dt ; or q = C uc(t)
d'où i(t) = -C d
uc(t)/dt
uC =r i(t) = -rCd uc(t)/dt
; rCd uc(t)/dt
+ uC =0.
Que
devient entre la date t=0 et t = 9 ms, l'énergie initialement stockée
dans le condensateur ?
L'énergie initialement stockée par le condensateur est dissipée sous
forme de chaleur ( effet Joule) dans le circuit lors de la décharge du
condensateur.
Seconde partie :
Le
condensateur après avoir été à nouveau chargé, est branché aux bornes
d'une bobine d'inductance L et de résistance r'. Le graphe suivant
donne la tension uc(t) aux bornes du condensateur.
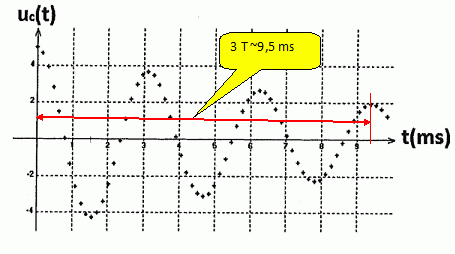
Déterminer graphiquement la valeur de la pseudo-période T.
T = 9,5 /3 = 3,2 ms = 3,2 10-3 s.
En déduire une valeur approchée de l'inductance( en henry H ) de la bobine.(20 ; 2 ; 0,2 ; 0,02 )
T = 2 p (LC)½ ; L = T2 / (4p2C) = (3,2 10-3)2/ (4*3,142*10-6) =0,25 H.
Faire
le schéma du montage comportant le condensateur et la bobine. Flécher
les tensions et indiquer le sens du courant positif i choisi.
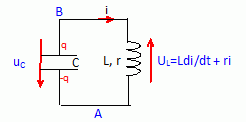
Préciser la relation entre UC et UL.
UC + UL = 0.
En déduire l'équation différentielle à laquelle obéit UC.
i = -dq/dt ; q = - CUC ; i = CdUC/dt ; di/dt = Cd2UC / dt2.
Par suite : UC +LCd2UC / dt2= 0.
Que devient, entre la date t=0 et la date t = 1,5 ms, l'énergie initialement stockée par le condensateur ?
[
0 ; 0,75 ms] : le condensateur se décharge à travers la bobine : la
majeur partie de l'énergie est stockée par la bobine. Une partie de
l'énergie est dissipée en chaleur dans les parties résistives.
[ 0,75 ; 1,5 ms] : le condensateur se charge en sens inverse : la
majeur partie de l'énergie stockée par la bobine est alors transférée au condensateur. Une partie de
l'énergie est dissipée en chaleur dans les parties résistives.
|
Troisième partie.
Le
condensateur après avoir été à nouveau chargé, est branché aux bornes
d'une bobine d'inductance L et de résistance r' en série avec un dipôle inconnu. Le graphe suivant
donne la tension uc(t) aux bornes du condensateur.
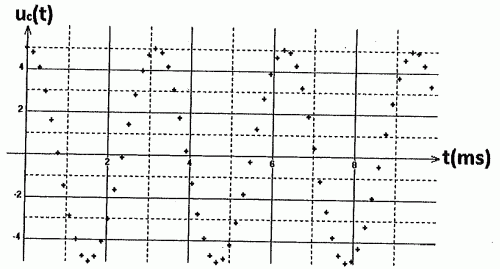
Quelle est la nature de ce dipôle inconnu ? Quel est son rôle ?
Le
régime est sinusoïdal non amorti. Le dipôle inconnu simule une
résistance négative. Ce dipôle compense à chaque instant les pertes
d'énergie par effet Joule.
|





