Aurélie 28/04/10
 

 

Supercondensateur, énergie hydraulique, énergie thermique, concours technicien de l'industrie et des mines 2009.



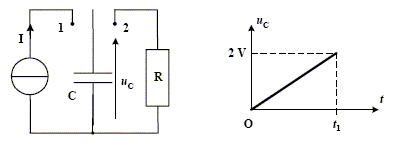
Dans le problème suivant, on utilise un supercondensateur de capacité élevée C = 1800 F.

Ce condensateur de 400 g a un diamètre de 50 mm et une hauteur de 150 mm.

A l’instant t = 0, on place l’interrupteur en position 1. On charge alors ce condensateur à l’aide d’un générateur de courant qui permet de délivrer une intensité constante I = 100 A. On obtient la courbe de charge ci-dessous.


  
  1. À quel instant t1 la tension aux bornes du condensateur atteint U1=2V ?
  2. Quelle est l’énergie Ec1 emmagasinée par ce condensateur à cet instant t1 ?
    A l’instant t = t1, on place l’interrupteur en position 2. On décharge ce condensateur à travers une résistance R = 2 W jusqu’à l’instant t2 où uC(t2) = U2= 1,5 V.
    L’équation donnant la tension aux bornes du condensateur durant cette décharge est : uC = A + B exp (-(t-t1) / t).
  3. Déterminer A, B et t.
  4. A quel instant t2 la tension aux bornes du condensateur atteint U2=1,5 V ?
  5. En supposant que la décharge du condensateur se passe sans pertes d’énergie, quelle est l’énergie ER dissipée par effet Joule dans la résistance R entre t1 et t2 ?
    En déduire la puissance moyenne PR dissipée par effet Joule dans la résistance R entre t1 et t2.
    On définit le rendement comme le rapport entre l’énergie restituée lors de la décharge et l’énergie emmagasinée lors de la charge. Les accumulateurs traditionnels du type batterie de voiture ont un rendement de l’ordre de 50 %. On mesure la puissance moyenne dissipée par R entre t1 et t2. On obtient 1,4 Watt.

Calculer le rendement h de ce supercondensateur. Comparer et conclure.  

Instant t1 où la tension aux bornes du condensateur atteint U1=2V :
Expression de la charge d'une armature : Q= It et Q= CuC.
It =CuC ; t = C/I uC.
t1 = 1800/100*2 = 36 s.

Energie Ec1 emmagasinée par ce condensateur à cet instant t1 :
Ec1 =½CuC2 = 0,5*1800*4 = 3,6 103 J.
A l’instant t = t1, on place l’interrupteur en position 2. On décharge ce condensateur à travers une résistance R = 2 W jusqu’à l’instant t2 où uC(t2) = U2= 1,5 V.
L’équation donnant la tension aux bornes du condensateur durant cette décharge est : uC = A + B exp (-(t-t1) / t).

Détermination de A, B et t :
A l'instant t = t1, uC=2 V : 2=A+B.
Quand t tend vers l'infini, le condensateur est déchargé : uC=0 : 0 = A ; B=2.
t= RC = 2*1800 ; t= 3600 s.

Instant t2 où la tension aux bornes du condensateur atteint U2=1,5 V :
ln(uC/2) =-(t2-t1) / t ; t ln(2/uC) =t2-t1 ; t2=t1+ t ln(2/uC)
t2=36+ 3600 ln(2/1,5) ; t2= 1,07 103 s.

En supposant que la décharge du condensateur se passe sans pertes d’énergie, l’énergie ER dissipée par effet Joule dans la résistance R entre t1 et t2 vaut :
énergie finale stockée - énergie initiale stockée = ½C ( 22-1,52)

ER = 900 (4-2,25) ; ER = 1,57 103 J
Puissance moyenne PR dissipée par effet Joule dans la résistance R entre t1 et t2 :
PR = ER /(t2-t1) = 1,57 103 / (1070-36) ; PR = 1,52 W.

On définit le rendement comme le rapport entre l’énergie restituée lors de la décharge et l’énergie emmagasinée lors de la charge. Les accumulateurs traditionnels du type batterie de voiture ont un rendement de l’ordre de 50 %. On mesure la puissance moyenne dissipée par R entre t1 et t2. On obtient 1,4 Watt.
Rendement h de ce supercondensateur :
h = 1,4/1,52*100 ; h = 92 %, valeur bien supérieure au rendement d'un accumulateur.
Energie hydraulique.
Un lac artificiel, créé par un barrage, contient un volume V = 1,2 109 m3 d'eau à l'altitude moyenne z1 = 1250 m. Au pied du barrage, à une altitude z2 = 1020 m, une usine hydro-électrique est alimentée par la retenue d'eau. Le débit d'eau alimentant les turbines est D = 100 m3 s-1. On néglige les pertes d'énergie par frottement dans les conduites. Les altitudes z sont comptées à partir du niveau dea mer pris comme référence pour l'énergie potentielle.
Déterminer l'énergie potentielle de pesanteur moyenne de l'eau en réserve dans le lac.
Ep1 = mgz1  ; masse de 1 m3 d'eau : 103 kg.
Ep1 = 1,2 1012 *9,8*1250 =1,47 1016 ~1,5 1016 J.
Quelle masse d'eau M arrive aux turbines en Dt =10 s ?
M = D reau Dt = 100*1000*10 = 1,0 106 kg.
Justifier que pour la masse d'eau considérée, la somme de l'énergie cinétique et de l'énergie potentielle de pesanteur Ec + Ep reste constante.
On néglige les pertes d'énergie par frottement dans les conduites ; seul le poids de l'eau travaille.
Le poids étant une force conservative, l'énergie mécanique Ec+Ep  de la masse d'eau reste constante.
On admet que l'énergie cinétique de l'eau à l'altitude z1 est nulle.
Déterminer l'énergie cinétique de la masse M de l'eau à l'entrée de la turbine à l'altitude z2. En déduire la vitesse de cette masse d'eau.
L'énergie mécanique initiale est sous forme potentielle de pesanteur : Ep1=Mgz1.
L'énergie mécanique finale est sous forme cinétique et potentielle : Ec + Mgz2.
L'énergie mécanique se conserve : Ec + Mgz2 = Mgz1 ; Ec = Mg(z1-z2)
Ec = 106 *10 (1250-1020)=2,3 109 J.
½Mv2 = 2,3 109 ; v = (2*2,3 109 / 106 )½ =67,82 ~68 m/s.
En considérant que la vitesse de l'eau est négligeable à la sortie de la turbine devant sa vitesse d'introduction,
calculer le travail fourni par la masse d'eau à la turbine. Quelle est sa puissance ?
La variation de l'énergie cinétique est égal aux travaux des forces.
0-Ec = W = - 2,3 109 J.
Le travail reçu par la machineest égal à 2,3 109 J. La puissance est égale au travail divisée par la durée correspondante.
P = 2,3 109 / 10 = 2,3 108 W.
l'usine hydro-électrique transforme 90 % de cette puissance en puissance électrique.
Calculer la puissance électrique fournie au réseau.
0,9 * 2,3 108 = 2,07 108 ~2,1 108 W.



Energie thermique.
En France, une partie de l'acier est fabriquée directement à partir des ferrailles de récupération. Cette ferraille est traitée dans des fours électriques à arc. Chaque convertisseur contient 310 t de fer. Le fer fond  à 1535 °C sous la pression atmosphérique normale. Sa chaleur latente massique de fusion est Lf = 270 kJ kg-1 ;  sa capacité thermique massique est C = 448 J kg-1 K-1 à l'état solide.
Calculer la quantité de chaleur nécessaire pour que le fer passe de 20°C à 1535 °C tout en restant solide.
Q1 = m C (qf-qi) = 3,1 105 *448 (1535-20) =2,1 1011 J.
Calculer la quantité de chaleur nécessaire à la fusion du fer à 1535 °C.
Q2 = m Lf = 3,1 105 * 270 103 = 8,4 1010 J.
Calculer en kWh, l'énergie minimale qu'il faut fournir au four électrique pour faire fondre le fer du convertisseur.
 Q1 + Q2 =2,1 1011 + 8,4 1010 = 2,94 1011 J.
1 Wh = 3600 J ; 1 kWh = 3600*1000 = 3,6 106 J.
 2,94 1011 / 3,6 106  ~ 8,2 104 kWh.





menu