Etude du
filtrage.
La
tension de sortie de l'amplificateur d'instrumentation comporte des
composantes indésirables qu'il convient d'éliminer afin d'obtenir une
tension continue. C'est le rôle du filtre étudié dans cette partie. On
se place pour cette en régime sinusoïdale à la fréquence f. Le
montage est représenté ci-dessous.
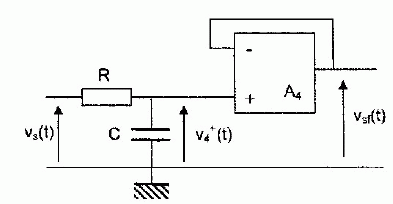
VS, V+4
et Vs sont
les expressions complexes des tensions vS(t), v+4(t)
et vs(t).
L'AO est considéré comme étant parfait.
Donner la
relation entre la fréquence f et la pulsation w en indiquant les unités.
w = 2 p f avec w ( rad/s) et f en Hz.
Ecrire
les expressions de l'impédance complexe ZC(jw) du condensateur et
son admittance complexe YC(jw).
ZC(jw)= 1 / (jCw) ; YC(jw) = jCw.
Déterminer l'expression de V+4
en fonction de R, C et Vs.
V+4
+ R i = Vs ; R i + ZC(jw) i = Vs ; i = Vs /(R+ZC(jw) )
V+4
= Vs -R i = Vs -RVs /(R+ZC(jw) )= Vs ( 1 -R / (R+ZC(jw) ) = Vs (ZC(jw) / (R+ZC(jw) ) =Vs / (1 + RYC(jw))
V+4 =Vs / (1 + jRCw) ; V+4 /Vs = 1 / (1 +
jRCw)
|
Etablir la relation
entre V+4
et Vsf .
Le montage avec l'AO est un suiveur : V+4 = Vsf .
|
Donner l'expression
de la fonction de transfert T(jw) =Vsf / Vs.
Vsf / Vs = V+4 /Vs = 1 / (1 +
jRCw) ; T(jw) =1 / (1 + jRCw).
On pose 1/(RC) = w0
; T(jw) =1 / (1 + j w/w0 ) = 1/(1+jf / f0)
Déterminer
le module T de la fonction de transfert.
T(jw) =(1-jf / f0) / [ 1 +(f / f0)2 ) ; T = 1/ [
1 +(f / f0)2 )]½.
En déduire
l'expression du gain G ( dB).
G = 20 log T = - 10 log [ 1 +(f / f0)2 ].
Le diagramme de Bode asymptotique du
gain est représenté ci-dessous.
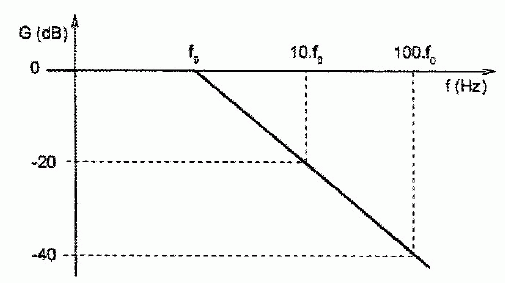
Comment
l'expression de G permet-elle de valider l'allure du diagramme ? Quelle
est la nature de ce filtre ? Quel est son ordre ?
C'est un filtre passe bas d'ordre 1.
Pour f << f0, le gain s'écrit : G ~-10 log 1) ~0;
asymptote horizontale d'équation G = 0 dB.
Pour f >> f0,
le gain s'écrit : G ~-10 log ((f / f0)2 ) ~-20 log (f / f0), droite décroissante de pente
-20 dB par décade.
L'atténuation est de 20 dB par décade dans la partie rejetée.
On donne R = 100 kW.
Calculer
C afin d'obtenir une atténuation de 40 dB à la fréquence de 10 Hz.
L'atténuation est de 20 dB par
décade dans la partie rejetée.
L'atténuation est de 40 dB pour deux décades : f = 100 f0.
f0 = f/100 = 10/100 = 0,1 Hz ; 1/(RC) = w0 = 2 p f0 = 0,628 rad/s.
C = 1/(0,628R) = 1/(0,628 105) = 1,6 10-5 F.
Convertion
analogique numérique.
La tension issue de l'amplificateur d'instrumentation doit
être convertie en nombre afin de pouvoir être traitée par le processeur
de l'ordinateur de plongée et affichée sur son écran. Cette
conversion est assurée par un convertisseur analogique ( CAN) 8 bits,
précédé d'un échantillonneur bloqueur comme l'indique la figure.
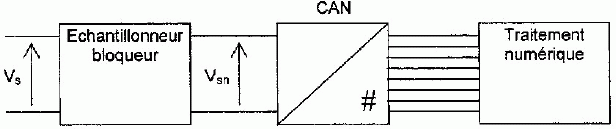
Quel
est le rôle de l'échantillonneur bloqueur ?
Le rôle de l'échantillonneur bloqueur est de maintenir la tension
constante pendant pendant la durée de conversion du signal analogique
en numérique.
Combien
de combinaisons de sorties un CAN 8 bits peut-il présenter ?
Il existe 28 combinaisons de sortie possibles soit : 28=
256.
Le CAN convertit des tensions comprises entre 0 et 9 V.
Quelle
est sa résolution analogique ?
9 / 256 = 0,035 = 35 mV ou 0,35 m.
Sachant qu'en sortie de l'amplificateur d'instrumentation
d'instrumentation une tension vs= 1 V est l'image d'une
profondeur de 10 m,
quelle
est la plus petite variation de profondeur mesurable ?
1 V correspond à 10 m ; 0,035 V correspond à 0,035*10 = 0,35 m = 35 cm.
Quel est
le nombre binaire associé à une profondeur de 90 m ? Exprimer cette
valeur en hexadécimal.
90 m correspond à 9 volts.
La première combinaison correspond à zéro ; la plus grande correspond à
255 " en décimal".
255 = 1*27 + 1*26 + 1*25 + 1*24
+ 1*23 + 1*22 + 1*21 + 1*20
;
255 sécrit : 1111 1111 en binaire et FF en hexadécimal.
Même
question pour une profondeur de 60 m.
60 m correspond à 6 Vet 9 V correspond au nombre décimal 255 ;
255*6/9= 170 " en décimal"
170 = 1*27 + 0*26 + 1*25 + 0*24
+ 1*23 + 0*22 + 1*21 + 0*20
;
170 sécrit : 1010 1010 en binaire et AA en hexadécimal.
Quelle
serait la plus petite variation de profondeur mesurable avec un CAN 12
bits ?
Nombre de points 212 = 4096.
Résolution numérique : 1/4096 = 2,44 10-4.
Valeur maximale : 212 -1 = 4095.
Résolution analogique : 90 / 4096 = 0,24 m.


