Statique
des fluides.
On montre que
le coefficient de compressibilité isotherme d'une substance peut
s'écrire XT = 1 / µ . Dµ
/ DP où XT, P, µ, T sont respectivement le volume, la
pression, la masse volumique et la température, ceci dans l'hypothèse
où XT est indépendant de la température. Dµ
représente la variation de la masse volumique correspondant à la
variation de pression DP.
Quelle
est l'unité de XT dans le système S.I
?
1 / µ . Dµ
est sans unité ; DP est
en pascal ; XT est en pascal-1.
Dans le cas de l'eau de mer, XT =5 10-10 SI.
Calculer
la variation de masse volumique Dµ de l'eau pour une élévation de
pression DP = 106 Pa au voisinage de µ0. Conclure.
Dµ = XT µ0 DP = 5 10-10* 999,98 * 106
=0,50 kg m-3.
Variation relative : 0,50 / 999,98 = 5 10-4 ( 0,05 %)
Dans le domaine considéré, l'eau est pratiquement incompressible.
On rappelle la realtion fondamentale de la
statique des fluides dans le champ de pesanteur terrestre : dP / dz =
-µg.
Avec µ masse volumique du fluide et z altitude comptée sur un axe
orienté vers le haut.
On considèrera par la suite que l'eau est un liquide
incompressible de masse volumique µ = 1000 SI. Le champ de pesanteur
est supposé uniforme avec g = 9,8 m s-2. On choisit
l'origine des altitudes à la surface de l'eau où la pression est P0
= 105 Pa.
Montrer
qu'à la profondeur z < 0 la pression est donnée par l'expression P(z)
= P0-µ0 g z.
dP = -µ0g dz ; intégrer entre 0 et z :
P(z) - P0 = -µ0g z ; P(z) = P0 -µ0g z.
A.N : z = -30 m ; P(z) = 105 - 103*9,8*(-30) =
3,94 105 ~ 4 105 Pa.
Dans l'eau, tous les 10 m, la pression augmente
d'environ 1 bar.
|
Plongée
autonome avec bouteille.
Remplissage de la
bouteille.
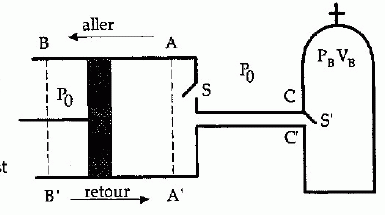
Afin d'effectuer le remplissage d'une bouteille de plogée à paroi
indéformable de volume VB, on utilise un compresseur
constitué d'un cylindre, de deux soupapes S et S' et d'un piston mobile
sans frottement entre les positions extrèmes AA' et BB'.
|
Lors de
l'aller du piston, la soupape S est ouverte alors que s' est fermée ;
on a alors l'admission de l'air atmosphérique dans le cylindre à la
pression P0.
Lors
du retour, la soupape S se ferme et la soupape s' s'ouvre dès que la
pression dans le cylindre devient supérieure à celle de la bouteille PB.
Quand le piston est en AA', le volume limité par le piston et la
section CC' est Vmin ; quand le piston est en BB', ce volume
est égal à Vmaxi.
Les transformations de l'air sont isothermes ; les températures dans le
cylindre, la bouteille et l'air extérieur sont &gales à Ta
; l'air est assimilé à un gaz parfait. R = 8,31 J K-1 mol-1.
La pompe n'ayant pas encore fonctionné, l'état initial du système est
le suivant :
- Bouteille : PB = P0.
- cylindre : pression P0; piston en BB'.
Le piston se déplace jusqu'en AA'.
Déterminer, en
fonction de P0, VB, Vmin, Vmaxi,
la pression P1 dans la bouteille à la fin de ce déplacement.
Loi de Mariotte : P0 (Vmaxi +VB ) = P1 (VB + Vmini) ; P1= P0 (Vmaxi +VB ) / (VB + Vmini).
A.N : P0 = 105 Pa ;
Vmini = 0,02 L ; Vmaxi = 2 L ; VB = 5
L ; Ta = 293 K.
P1= 105* 7 / 5,02 = 1,4 105 Pa.
Après n coups de pompe, on peut montrer que la pression Pn
dans la bouteille vérifie la realtion : P0 Vmaxi +Pn-1VB = Pn (VB + Vmini)
avec Pn-1 la pression dans la bouteille après n-1 coups
de pompe.
Le graphe ci-dessous montre l'évolution de la pression dans la
bouteille en fonction du nombre de coups de pompe donnés.
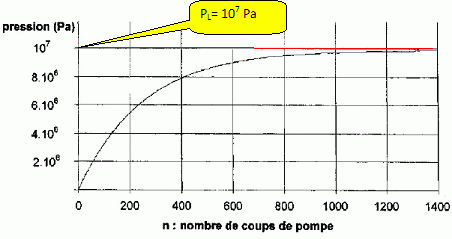
Retrouver
l'expression de PL en fonction de P0, Vmin
et Vmax à partir de l'expression donnant Pn.
P0 Vmaxi +Pn-1VB = Pn (VB + Vmini) ; on pose A = VB + Vmini ; B = Vmaxi +VB ;
n = 1 : P0 Vmaxi +P0VB =AP1 ; P1= BP0 / A + P0VB / A.
n = 2 : P0 Vmaxi + P1VB =A P2 ; P2= P0 Vmaxi / A + BP0 VB / A2 + P0V2B / A2.
n = 3 : P0 Vmaxi + P2VB =A P3 ; P3= P0 Vmaxi / A + P0 VBVmaxi / A2 + BP0 V2B / A3 + P0V3B / A3.
Pn= P0 Vmaxi / A [ 1 + VB / A +(VB / A)2+.......+ (VB / A)n-2 + BP0 Vn-1B / An + P0VnB / An.
Les deux derniers termes tendent vers zéro, le dénominateur étant
supérieur au numérateur.
VB / A +(VB / A)2+.......+ (VB / A)n-2 suite géométrique de raison q=VB / A, de premier terme a = VB / A .
La somme des terme vaut : a(1-qn-2) / ( 1-q) ; q est
inférieur à 1 : qn-2tend vers zéro.
a(1-qn-2) / ( 1-q) ~ a / (1-q) = VB
/ (A-VB).
1+VB / (A-VB) =A / (A-VB) ;
PL= P0 Vmaxi /(A-VB) = P0 Vmaxi / Vmini= 105 *2 / 0,02 = 107 Pa.
On retrouve la valeur du graphique.
Plongée avec
détendeur.
On fera l'hypothèse que , en plongée,
la pression dans l'eau obéit à la loi précédemment établie : P(z) = P0
- µ0gz.
Le détendeur, inséré entre bouteille et la bouche du plongeur assure
plusieurs fonctions :
- il réduit la pression de l'air issu de la bouteille à la pression
P(z) de l'endroit où se trouve le plongeur ;
-il fournit la quantité d'air nécessaire à la respiration du plongeur ;
- il se bloque lorsque la pression pB de l'air dans la bouteille
devient de l'ordre de la pression critique PC en dessous de
laquelle il ne faut pas descendre pour raisons de sécurité.
Au début de la plongée, la bouteille de volume VB est
remplie d'air à la température Ta sous la pression P.
Calculer
le nombre de moles d'air ni contenues dans la bouteille si PB
= 107 Pa.
Loi des gaz parfaits : ni = PB VB / (RTa)
=107*5 10-3 / (8,31 *293) =20,54 mol ~ 20 mol.
Lorsque le détendeur se bloque, la pression dans la bouteille devient PC
= 4 105 Pa.
Calculer
le nombre de moles d'air nF restant dans la bouteille.
nF = PC
VB / (RTa) =4 105*5 10-3 /
(8,31 *293) =0,82 mol ~ 0,8 mol.
En
déduire le volume V de gaz que peut respirer le
plongeur à la profondeur z.
n = ni -nF =20,54
- 0,82 = 19,72 mol
V = nRT / P(z) avec P(z) = 3,94 105 à la profondeur de 30 m.
V = 19,72 *8,31*293 / 3,94 105 =0,122 m3 ~0,12 m3.
Les poumons ont une capacité VP et la fréquence de
respiration du plongeur est f.
En
déduire, en fonction de V, VP et f la durée Dt de plongée avant que le
détendeur se bloque.
En T = 1/f seconde le plongeur absorbe un
volume VP d'air ; en Dt seconde le plongeur absorbe un
volume V d'air.
Dt = V T / Vp = V
/( VPf ).
A.N : Vp = 2 L ; f = 0,2 s-1.
Dt =122 / (2*0,2)
=305 s ~ 5 min.
|

