Masse
volumique et densité.
Rappeler
l'expression de la masse volumique ; quelle est son unité dans le
système SI ?
Je calcule une masse volumique en divisant une masse par un volume :
masse ne kg, volume en m3 et masse volumique en kg m-3.
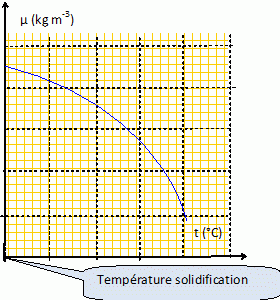
Le graphe ci-dessous représente les variations de la masse volumique de
l'eau liquide en fonction de la température. La courbe présente un
maximum pour une température de 4°C et une masse volumique µ0
= 999,98 SI.

Par rapport à la plupart des autres corps, ce graphe présente une
anomalie. Quelle
est-elle ?
La masse est constante ; le volume augmente avec
la température : la masse volumique diminue quand la température
augmente.
En général, la masse volumique est maximale à la température de
solidification ; par contre pour l'eau le maximum se situe à 4 °C et
non pas à la température de solidification 0°C.
Donner
l'allure de ce graphe dans la plupart des corps.
|
Interpréter
l'expérience suivante.
Lors du refroidissement de l'huile, celle-ci se solidifie d'abord par
le bas, alors que dans le cas de l'eau, la glace se forme d'abord
en haut.
La masse volumique de la glace est inférieure à celle du liquide : la
glace flotte sur l'eau.
La masse volumique de l'huile solide est supérieure à celle du liquide
: le solide coule.
On entend dire que l'eau des lacs ne peut geler totalement en
profondeur ; proposer
une explication.
Les lacs présentent une stratification thermique verticale. La densité
du liquide est maximale au fond et la température est de 4 °C.
|
Densité.
On définit la densité d'un liquide ou d'un solide par rapport à l'eau.
La densité est le rapport de la masse d'un certain volume du solide ou
du liquide à la masse du même volume d'eau pris à 4°C sous pression
atmosphérique normale.
Pour
quelle raison la température est-elle précisée ?
La masse volumique du corps de référence, l'eau, dépend de la
température.
Pour
quelle raison la pression est-elle précisée ? Est-ce déterminant ?
Pourquoi ?
La masse volumique dépend de la pression. C'est particulièrement vrai
dans le cas des gaz qui sont compressibles. Par contre les
liquides et les solides sont pratiquement incompressibles et dans ce
cas la masse volumique dépend peu de la pression.
Quelle
est l'unité de la densité ?
La densité étant le rapport de deux masses volumiques est sans unité.
Quelle
relation simple existe t-il entre masse volumique et densité ?
La densité est le rapport de la masse volumique du solide ou du liquide
à la masse volumique ( à 4°c ) de l'eau, corps de référence..
La densité a même valeur que la masse volumique du liquide ou du solide
exprimée en g cm-3.
Quel est
l'intérêt pratique de cette grandeur ?
Dans le cas de deux liquides non miscibles, le plus dense occupe la
partie inférieure d'une ampoule à décanter.
Un solide de densité inférieure à un liquide, flotte ; un solide de
densité supérieure à un liquide, coule.
Que
peut-on dire de la densité de l'eau du robinet par rapport à celle de
l'eau distilée ? Justifier.
L'eau du robinet contient de nombreux ions en plus des molécules d'eau
; l'eau distillée ne contient que des molécules d'eau.
La densité de l'eau du robinet est supérieure à celle de l'eau
distillée.
.Mesure de la
densité de la glace.
Etude statique.
On se place à la surface terrestre. L'intensité du champ de pesanteur
est noté g. On considère un récipient contenant de l'eau pure à 4°C. Un
glaçon cubique d'arrète c, de masse volumique µ1 flotte
immobile à la surface de l'eau de masse volumique µ0. On
fait l'hypothèse que le glaçon ne fond pas et on note h la hauteur
immergée.
Quelles
sont les forces exercées sur la glaçon ?
Le poids mg = c3µ1g et la poussée
d'Archimède de valeur c2hµ0g, se
neutralisent.
c3µ1g = c2hµ0g soit : cµ1
=hµ0 ;
En
déduire l'expression de la densité de la glace en fonction de c et h.
d = µ1 /µ0 = h/ c.
A.N : h = 80 mm et c = 87 mm
d = 80/87 =0,92.
Etude dynamique.
A partir de la situation précédente, on appuie légèrement sur le glaçon
de sorte de l'immerger davantage et on l'abondonne à lui même sans
vitesse initiale.
Montrer
qualitativement que celui-ci va osciller.
Juste après le lâcher, la poussée d'Archimède est supérieur au poids :
le glaçon remonte et passe à la position d'équilibre avec une vitesse
verticale vers le haut ; il continue donc de monter, mais cette fois-ci
le poids devient supérieur à la poussée.
La vitesse va s'annuler et sous l'effet du poids, le glaçon redescend.
Il passe à la position d'équilibre avec une vitesse verticale dirigée
vers le bas ; il continue donc à descendre, mais cette fois-ci la
poussée devient supérieur à la poids. Il va finir par s'arrêter avant
de remonter et ainsi de suite.
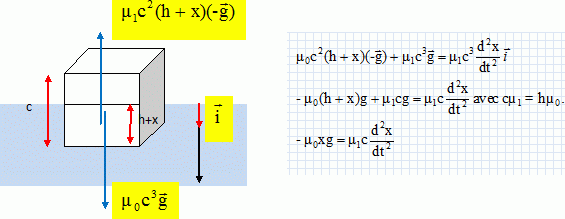
A un instant t quelconque, la hauteur immergée du glaçon est h+x. par
application de la seconde loi de Newton, en ne faisant intervenir que
les forces précédentes, montrer que le
mouvement du glaçon satisfait à l'équation différentielle : µ1
c d2x/dt2 + µ0 gx = 0.
Quelle
est la solution générale de l'équation différentielle ? On ne
cherchera pas à déterminer les constantes liées aux conditions
initiales.
d2x/dt2 + µ0g / (µ1c) x=0 ;
on pose w02
= µ0g / (µ1c)= g /(dc) avec d : densité de la
glace.
x = A cos (w0t +
B) avec A et B des constantes.
Donner la
période des oscillations du glaçon T0 en fonction de d
densité de la glace, g et c.
T0 = 2 pi / w0
= 2 pi ( dc / g) ½.
A.N : g = 9,8 m s-2 ; T0 = 0,57 s. d = g T02
4 pi2 / ( 4 pi2c) =9,8 *0,572
/ (4*3,142 *8,7 10-2) =0,93, valeur identique à
la valeur calculée ci-dessus ( erreur relative ~ 1%)
En fait le mouvement du glaçon s'amortit rapidemment. Proposer une
explication.
Il faut tenir compte des frottements fluides entre la glace et l'eau.
L'eau salée.
Quelle
est l'ordre de grandeur de la concentration massique en sels dissous de
l'eau de mer ? Quelles sont les mers les plus salées ?
La salinité est de l'ordre de 35 g/L dans les océans. En dehors de la
mer Morte, les mers les plus salées sont quasiment fermées, recoivent
peu d'eau douce et sont situées dans les régions chaudes ( la
Méditerranée par exemple).
Qu'est
qu'une solution saturée ? Quel est l'ordre de grandeur de la
concentration massique en chlorure de sodium correspondante à la
température ambiante ?
La solubilité s d'un corps (appelé soluté) est la masse de
soluté que l'on peut dissoudre dans un solvant pour obtenir un litre de
solution saturée.
La solution est saturée lorsque le solvant ne peut pas dissoudre la
totalité du soluté. Un partie de ce dernier reste au fond du récipient.
A température ambiante, la solubilité du chlorure de sodium est environ
350 g/L.
Pour
déterminer la concentration massique d'une eau salée, on réalise la
succession d'expériences ci-dessous à la température de 15 °C. On
utilise une balance électronique au gramme et une fiole jaugée de 1000
mL.
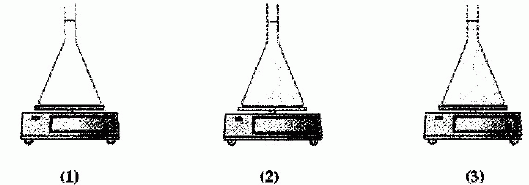
(1) fiole
jaugée seule : m1 = 256 g
(2) fiole jaugée remplie d'eau distillée : m2 = 1255 g
(3) fiole jaugée remplie d'eau salée m3 = 1278 g.
Dans le
cadre de cette mesure, faut-il prendre en compte le fait que l'eau ne
se trouve pas à 4°C mais à 15 °C ? Justifier.
Il faudrait tenir compte de la dilatation de l'eau et du verre de la fiole jaugée si on utilisait une balance de précision.
Or les pesées se font au gramme près ; dans ces conditions, travailler à 4 °C ou à 15 °C donnerait le même résultat.
Exprimer la densité
de l'eau salée en fonction de m1, m2 et m3.
d =masse de 1 L d'eau salée / masse de 1 L d'eau = (m3
-m1 ) / (m2-m1
) =1022 /
999 =1,023 ~ 1,02. ( trois chiffres significatifs).
Erreur relative sur (m3
-m1 ) et sur (m2-m1
) ~ 4 / 1000 = 0,4 % ; précision sur la densité : 0,8 %
d = 1,023 + ou - 0,004 ; 1,019 < d < 1,027.
En
se référant au tableau ci-dessous, déterminer de façon cohérente et le
plus précisément possible la concentration massique de la solution
d'eau salée.

A une densité d = 1,019 correspond une masse volumique égale à 1,019 103 kg m-3 à 15 °C
A une densité d = 1,027 correspond une masse volumique égale à 1,027 103 kg m-3 à 15 °C.
La concentration en NaCl serait donc comprise entre 30 et 40 g /L.




