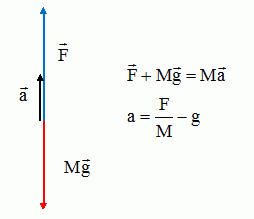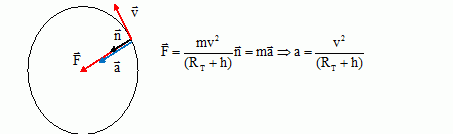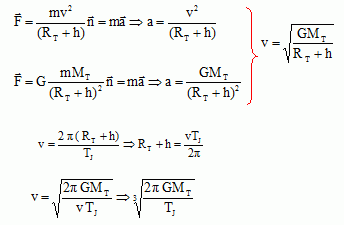On s'intéresse à la mise en orbite d'un satellite artificiel autour de la Terre. (8 points)
On donne : masse de la Terre MT = 5,98 1024 kg ; jour sidéral : TJ = 86164 s ; G = 6,67 10-11 S.I.
Un jour sidéral est la durée que met la Terre pour faire un tour sur
elle- même par rapport aux étoiles.
Etude de la phase de lancement.
Le satellite est placé sur une orbite circulaire à l'aide d'une fusée.
Le
lancement débute lors de la mise à feu des moteurs de la fusée.
L'ensemble de la fusée et du satellite ont alors une masse M = 2,34 106 kg.
Pendant les premières secondes suivant le lancement, on admet que
l'éjection du gaz par les moteurs a le même effet qu'une force
extérieure appelée poussée de valeur F =4,51 107 N. La
trajectoire par rapport au sol est verticale. On suppose que les
frottements et la diminution de masse de la fusée sont négligés,
l'intensité de la pesanteur ne varie pas et a pour valeur g = 9,81 m s-2.
Faire le bilan des forces (et les représenter sur un schéma ) s'exerçant sur la fusée juste après le décollage.
La fusée est soumise à :
- son poids, verticale, vers le bas, valeur Mg ;
- à la poussée des moteurs, verticale, vers le haut, valeur F supérieure au poids.
|
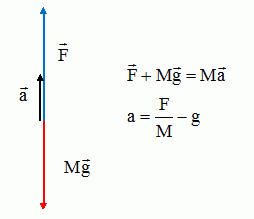
Donner les caractéristiques de l'accélération.
Ecrire la seconde loi de Newton sur un axe vertical ascendant : l'accélération est verticale, vers le haut,
valeur a = 4,51 107 / 2,34 106 -9,81 =9,4635 ~9,46 m s-2.
|
Calculer la distance d parcourue pendant Dt = 2,0 s suivant le décollage.
La vitesse est une primitive de l'accélération : v = at + v0 ;
à t = 0, la vitesse initiale est nulle : v0 = 0 ; v = at.
La position est une primitive de la vitesse : d = ½at2 + Cste.
à t = 0, l'altitude est nulle : d = ½at2.
d = 0,5*9,4635*22=18,927 ~ 19 m.
En déduire le travail de chaque force pendant Dt.
Le travail du poids est résistant en montée : WP = -Mgd = -2,34 106 *9,81 *18,927 = -4,3448 108 ~ -4,3 108 J.
La poussée et le déplacement sont colinéaires et de même sens ; le travail de la poussée vaut :
WF = Fd =4,51 107 *18,927 =8,536 108 ~ 8,54 108 J.
En déduire la vitesse acquise au bout de Dt.
Ecrire le théorème de l'énergie cinétique entre l'instant de décollage et Dt :
½Mv2 - 0 = WP +WF ; v = [2(WP +WF) / M]½.
v = [2(-4,3448 108 +8,536 108) / 2,34 106]½ = 18,93 ~18,9 m s-1.
Retrouver le résultat en exploitant la valeur de l'accélération.
v = a t = 9,4635*2 =18,93 ~18,9 m s-1.
Etude du satellite en orbite.
Le satellite a une masse m = 893 kg. Son orbite est circulaire à l'altitude h.
Préciser et définir le référentiel d'étude.
Le référentiel géocentrique : l'origine du repère est le centre de la
Terre et les trois axes pointent vers des étoiles lointaines qui
semblent fixes.
Montrer que le satellite a un mouvement uniforme.
Le satellite est soumis à la seule force de gravitation centripète ;
cette force, perpendiculaire à la vitesse, ne travaille pas :
l'énergie cinétique, et donc la vitesse, du satellite ne sont pas
modifiées.
La valeur de la vitesse étant constante, le mouvement est circulaire uniforme.
Le satellite possède t-il une accélération ? Si oui la représenter sur un schéma sans souci d'échelle.
La direction du vecteur vitesse change : le vecteur vitesse n'est pas
un vecteur constant : le satellite possède donc une accélération.
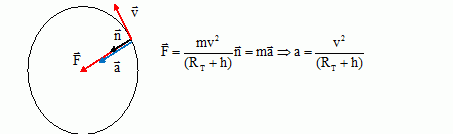
|
Définir le terme géostationnaire. Quelles conditions doit remplir un satellite pour être géostationnaire ?
Le satellite décrit un cercle dans le plan équatorial, dans le même sens que la Terre.
Sa période de révolution est égale au jour sidéral.
Il paraît donc fixe pour un observateur terrestre.
Exprimer la valeur de la vitesse du satellite en fonction de G, MT et TJ. Faire l'application numérique.
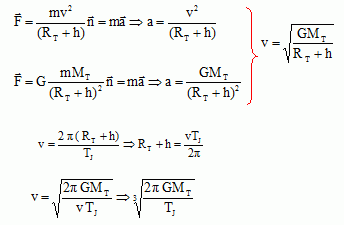
v = [6,28 *6,67 10-11*5,98 1024 /86164 ]1/3 =3,0753 103~3,08 103 m s-1.
Calculer pour ce satellite le rapport T2/r3 où T représente la période de son orbite et r le rayon de l'orbite.
3ème loi de Kepler : T2/r3 = 4 p2 / (GMT).
4 p2 / (GMT) = 4*3,142 / ( 6,67 10-11*5,98 1024 ) = 9,90 10-14s2 m-3.
Que vaut ce rapport pour la Lune. Expliquer.
La Lune est un satellite de la Terre ; l'astre central, la Terre, ne
change pas : ce rapport est identique pour la Lune et le satellite
artificiel de la Terre.
|
|