Un
oscillateur électrique est composé d'un conducteur ohmique de
résistance R, d'une bobine d'inductance L et d'un condensateur de
capacité C montés en série. ( 12 points)
Chaque dipôle est étudié séparément afin de constituer l'oscillateur.
Le conducteur ohmique.
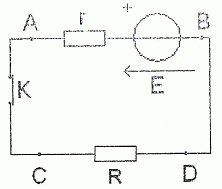
E = 4,0 V ; r = 20 W.
Recopier le schéma et y indiquer les branchements de l'oscilloscope nécessaires à la visualisation de la tension UCD.
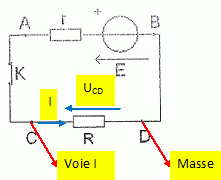
L'interrupteur K étant fermé, l'exploitation de l'oscillogramme donne UCD = 3,5 V.
En déduire la valeur de R.
Additivité des tensions : rI +R I = E = 4,0 V ; (20 + R) I = 4
et R I = 3,5 V ; I = 3,5 / R d'où : (20 + R) 3,5 = 4 R ; 20*3,5 = 0,5 R ; R = 140 W.
Dessiner l'allure de la tension UCD au cours du temps.
|
Comment vérifier avec l'oscilloscope que la force électromotrice est bien 4 V ?
Visualiser la tension UAB = E, lorsque l'interrupteur est ouvert.
|
Le condensateur.
On souhaite déterminer la capacité C du condensateur.
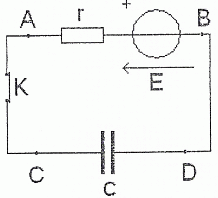
Le condensateur étant déchargé, à t=0, on ferme l'interrupteur K, ce qui déclenche l'acquisition de la tension uCD à l'oscilloscope.
Etablir l'équation différentielle relative à la tension UCD.
Additivité des tensions : E = r i + UCD ; i = dq /dt avec q = CUCD d'où i = C d UCD/ dt.
E = r C d UCD/ dt + UCD ;
d UCD/ dt + UCD / (rC) = E/(rC).
Résoudre l'équation différentielle.
On pose t, constante de temps : t = rC.
Solution générale de l'équation sans second membre : UCD = A exp(-t/t) ;
Solution particulière de l'équation différentielle ( régime permanent ) : UCD = E.
Solution générale de l'équation différentielle : UCD = A exp(-t/t) + E.
A t = 0, le condensateur est déchargé : UCD=0 = A +E d'où A = -E.
UCD = E(1- exp(-t/t)).
Dessiner l'allure de la tension UCD au cours du temps. Expliquer, à l'aide de la courbe comment déterminer t.
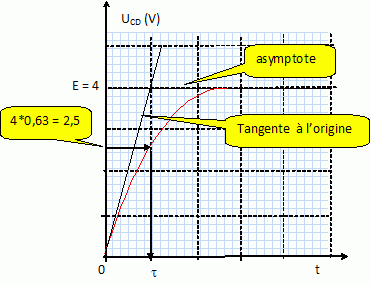
La lecture de la constante de temps t sur la courbe affichée à l'oscilloscope donne t = 5,3 ns.
Déduire la valeur de C.
5,3 10-9 = 20 C ; C = 5,3 10-9 / 20 = 2,65 10-10 ~ 2,7 10-10 F.
Déterminer l'énergie emmagasinée par le condensateur entre les instants t1 = 1,0 ns et t2 = 2,0 ns.
uCD(t1) = 4 (1-exp(-1/5,3) = 0,6878 V
Energie stockée à la date t1 : ½C u2CD(t1) =0,5 *2,65 10-10 *0,68782 =6,268 10-11 J.
uCD(t2) = 4 (1-exp(-2/5,3) = 1,2573 V
Energie stockée à la date t2 : ½C u2CD(t1) =0,5 *2,65 10-10 *1,25732 =2,0946 10-10 J.
Puis : 2,0946 10-10 - 6,268 10-11 =1,4677 10-10 ~1,5 10-10 J.
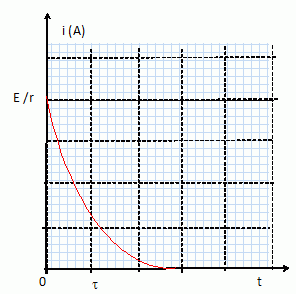
Etablir l'expression de l'intensité du courant débité par le générateur au cours du temps, en fonction de E, r et C.
Tracer sans souci d'échelle l'allure de la courbe représentant i(t).
i = C d UCD/ dt avec d UCD/ dt = E/(rC)exp(-t/t) ; i(t) = E/r exp(-t/t).
La bobine.
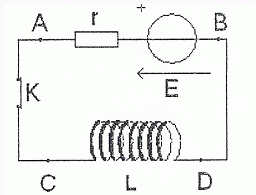
A t = 0, on ferme l'interrupteur K, ce qui déclenche une acquisition de la tension UCD à l'oscilloscope.
On suppose que la bobine n'a pas de résistance.
Quelle mesure à l'oscilloscope peut montrer que la résistance de la bobine est négligeable devant r ?
En régime permanent la bobine se comporte comme un conducteur ohmique.
Si la résistance de la bobine est négligeable devant r, alors UCD est voisin de zéro en régime permanent.
Etablir l'expression de la tension UCD au cours du temps en fonction de E, r et L.
Additivité des tensions : E = r i + Ldi/dt avec UCD = Ldi/dt.
di/dt + r/L i = E/L.
On pose t, constante de temps : t = L/r.
Solution générale de l'équation sans second membre : i = A exp(-t/t) ;
Solution particulière de l'équation différentielle ( régime permanent ) : I = E/r.
Solution générale de l'équation différentielle : i = A exp(-t/t) + E/r.
A t = 0, l'intensité est nulle : i=0 = A +E/r d'où A = -E/r.
i = E/r(1- exp(-t/t))= 4 /20(1-exp(-t/t)) =0,2 (1-exp(-t/t))
UCD = Ldi/dt avec di/dt = E/L exp(-t/t) ; UCD =E exp(-t/t).
Dessiner l'allure de la courbe représentant cette tension.
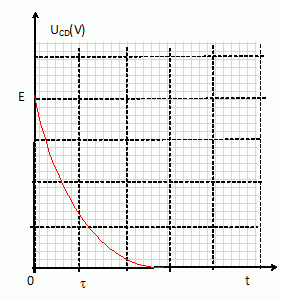
Calculer la constante de temps sachant que L = 32 mH.
t = L/r = 0,032 /20 =1,6 10-3 s. ( 1,6 ms )
Déterminer l'énergie emmagasinée par la bobine entre les instants t1 = 0,32 ms et t2 = 0,64 ms.
i(t1) = =0,2 (1-exp(-0,32 / 1,6)) = 3,625 10-2 A.
Energie stockée à la date t1 : ½L i2=0,5 *0,032 *(3,625 10-2 )2 =2,1316 10-5 J.
i(t2) = =0,2 (1-exp(-0,64 / 1,6)) = 6,594 10-2 A.
Energie stockée à la date t2 : ½L i2=0,5 *0,032 *(6,594 10-2 )2 =6,956 10-5 J.
Puis : 6,956 10-5 - 2,1316 10-5 = 4,825 10-5 ~4,8 10-5 J.
|
L'oscillateur électrique.
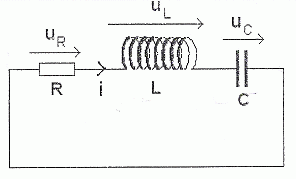
Etablir l'équation différentielle de la charge q du condensateur.
Additivité des tensions : UR + UL + UC = 0 ; avec q = -CUC.
UR = -Ri ; UL =-Ldi/dt et i = dq/dt ; di/dt = d2q/dt2.
Par suite : -Rdq/dt -Ld2q/dt2-q/C = 0
Ld2q/dt2+Rdq/dt +q/C = 0
d2q/dt2 +R/Ldq/dt + q/(LC) = 0.
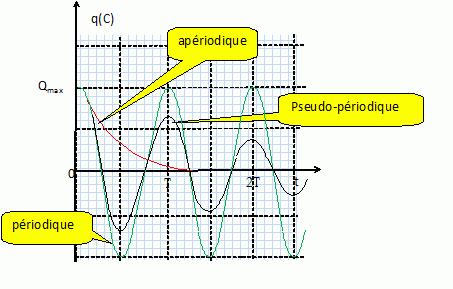
Quels sont les régimes possibles pour un tel circuit ? Donner l'allure de la courbe q(t) pour ces différents régimes.
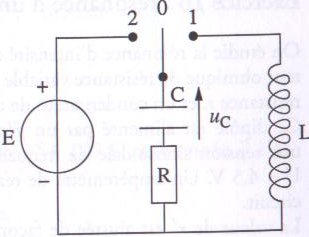
Expliquer
comment on peut expérimentalement visualiser à l'oscilloscope, les
oscillations libres et amorties de cet oscillateur. Faire notamment le schéma du montage expérimental.
Remplacer R par une résistance variable
; charger le condensateur ( interrupteur en position 2) ; puis basculer
l'interrupteur en position 1 ; visualiser la tension aux bornes
du condensateur.
|
|










