Analogies entre oscillateurs électrique et mécanique, photons, solide sur une piste circulaire, concours orthoptie Toulouse 2004.

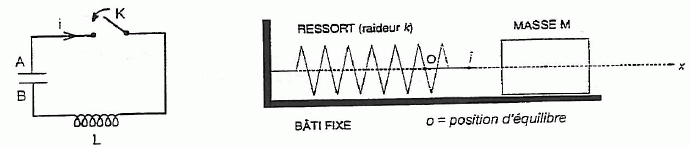
Conditions initiales : charge qA du condensateur qA =- QB = Qm positive ; l'interrupteur K est ouvert. Le solide est initialement au repos et dans la position d'élongation maximale x(0) = Xm positive. On le lâche à t=0. Etablir l'équation différentielle régissant la charge du condensateur.  uAB = Ldi/dt = 0 avec uAB = QA / C et i = dQB/dt = -dQA/dt ; di/dt = -d2QA/dt2. QA / C +Ld2QA/dt2 = 0 ; d2QA/dt2 +QA / (LC) = 0 On pose w02 = 1/(LC) : d2QA/dt2 + w02QA =0. Etablir l'équation différentielle régissant l'élongation  du solide. 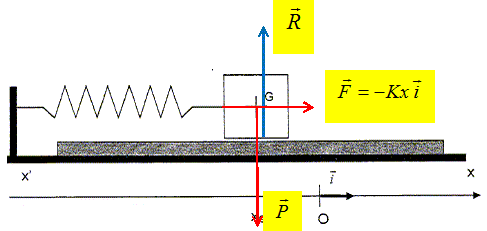P : poids ; R : action du support ; F : force de rappel. En projetant sur l'axe x'x la relation entre vecteurs traduisant la seconde loi de Newton appliquée sur le mobile, on établit la relation entre K, m, x et ax = d2x/dt2. -Kx = m d2x/dt2 ; d2x/dt2 + K/m x = 0. On pose w02 =K/m. d2x/dt2 +w02 x = 0.   Quelle est la période propre de ces deux oscillateurs ?  T0 = 2 p / w0 ; T0 = 2 p (LC)½ ; T0 = 2 p (m/K)½. Etude énergétique du circuit LC.  Donner l'expression de l'énergie emmagasinée dans le condensateur. EC(t) = ½QA2/C. Donner l'expression de l'énergie emmagasinée dans la bobine. EL(t) = ½Li2. Que peut-on dire de la somme EC(t)+ EL(t) ? Dans la mesure où la résistance de la bobine est négligeable, la somme EC(t)+ EL(t) est constante, égale à l'énergie initiale, c'est à dire ½Qm2/C. Etude énergétique du pendule mécanique.  Donner l'expression de l'énergie potentielle du ressort. Ep(t) = ½kx2. Donner l'expression de l'énergie cinétique du pendule. Ec(t) = ½m v2. Que peut-on dire de la somme Ep(t)+ Ec(t) ? Dans la mesure où les forces de frottement sont négligeables, la somme Ep(t)+ Ec(t) est constante, égale à l'énergie initiale, c'est à dire ½kXm2. L'analyse du spectre d'émission d'une lampe à vapeur de sodium révèle la présence de raies de longueurs d'onde bien définies. Justifier la discontinuité du spectre. L'énergie de l'atome est quantifiée, seules quelques valeurs sont possibles. Indiquer à quelle transition correspond pour l'atome de sodium, l'émission de la raie jaune de longueur d'onde l = 589,0 nm. 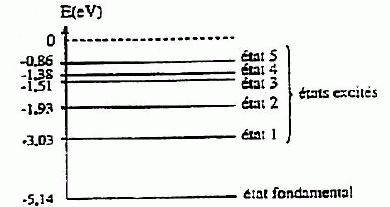La différence d'énergie entre les deux niveaux est DE = hc/l = 6,62 10-34 *3 108 / 589 10-9 = 3,37 10-19 J. 3,37 10-19 / 1,6 10-19 = 2,11 eV. C'est la différence d'énergie entre le niveau fondamental et l'état excité 1. L'émission de la raie jaune correspond  du retour de l'atome excité ( n=2) à l'état fondamental ( n=1). Comment réagit un atome de sodium, initialement dans l'état fondamental, lorsqu'il interagit avec un photon de longueur d'onde l= 589,0 nm ? L'atome absorbe ce photon et passe dans le premier état excité. Que se passe t-il si l'atome de sodium, initialement dans l'état fondamental, reçoit un photon d'énergie 2,50 eV ? L'énergie du photon ne correspond pas à la différence d'énergie entre deux niveaux de l'atome : ce photon n'est pas absorbé par l'atome. L'atome reste à l'état fondamental. L'atome de sodium, dans son état fondamental, est heurté par un électron d'énergie 2,50 eV. Lors de l'interaction, l'atome de sodium reste pratiquement immobile et passe à un état excité. Quelle est l'énergie cinétique de l'électron après son interaction avec l'atome ? L'électron cède 2,11 eV à l'atome : ce dernier passe de l'état fondamental au premier niveau excité. L'énergie cinétique de l'électron après interaction vaut : 2,50-2,11 = 0,39 eV ou 0,39*1,6 10-19 = 6,24 10-20 J. Quelques instant après cette interaction, l'atome de sodium se désexcite en émettant un photon. Quelle est la longueur d'onde de celui-ci ? 589 nm. Un mobile de masse m, supposé ponctuel, peut glisser le long d'une piste ABC. Le mouvement  a lieu dans le plan vertical. 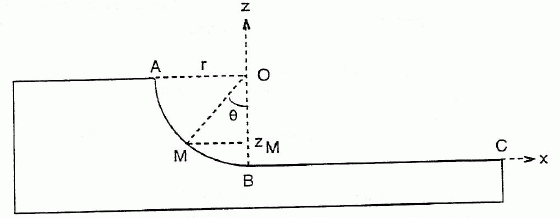La partie curviligne est un quart de cercle parfaitement lisse, de telle sorte que les frottements y sont négligeables. Le mobile est lancé en A avec une vitesse vA = 2 m/s, verticale et dirigée vers le bas. Etablir l'expression de la vitesse vM du mobile en un point quelconque du quart de cercle en fonction de vA, g, q, r et m. Le mobile est soumis à son poids et à l'action du support, perpendiculaire au support en l'absence de frottement. L'action du plan, perpendiculaire à la vitesse, ne travaille pas. Le travail du poids est moteur en descente : W = mg ( zA-zM). On choisi B comme référence des altitudes. zA= r ; zM = r(1-cosq) ; W = mg r cosq. Ecrire le théorème de l'énergie cinétique entre les points A et M : ½mv2M-½mv2A = mg r cosq. v2M= v2A +2g r cosq ; vM = ( v2A +2g r cosq)½. A.N : r = 1 m ; g = 10 m s-2 ; q = 30°. vM = ( 22 +20 cos30)½= 4,6 m/s. Etablir l'expression littérale du module de la réaction  de la piste puis la calculer. 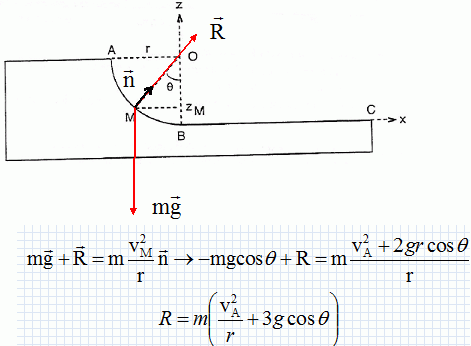(m = 150 g ) R = 0,15 ( 4 +30*cos30) =4,5 N. La portion BC est rectiligne et rugueuse. On peut assimiler les forces de frottements à une force unique, constante et opposée au mouvement. Sachant que vC = 2 m/s, calculer la valeur de la force de frottement. 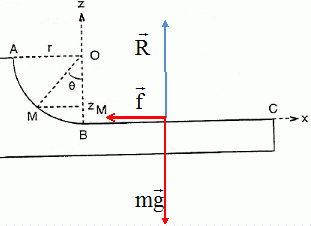BC = 2 m Entre B et C, le poids et l'action du plan, perpendiculaires à la vitesse ne travaille pas. Le travail des frottement est résistant et vaut -f BC. La vitesse en A est égale à la vitesse en C. Entre A et C, l'énergie cinétique ne change pas. Le théorème de l'énergie cinétique donne : mg r -fBC = 0 f = mgr / BC = 0,15*10*1 / 2 = 0,75 N. Calculer le travail des frottements sur la portion BC. -f BC = 0,75 * 2 = -1,5 J.

retour -menu