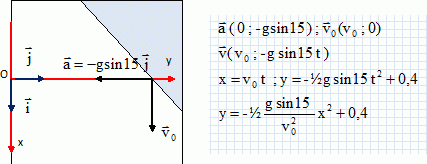Isotopes
du chlore.
A
l'état naturel le chlore compte 3 isotopes. Deux sont stables : le
cl-35 et le Cl-37. Le Cl-36 est radioactif et possède une demi-vie de
301 000 ans.
Qu'est-ce
qu'un isotope ? Que signifient les nombres 35, 36 et 37 ?
Deux isotopes ne se différencient que par leur nombre de neutrons. Ils
ont le même numéro atomique.
35, 36 et 37 représentent respectivement le nombre de nucléons des
isotopes 35Cl, 36Cl et 37Cl.
Sachant
que le numéro atomique du chlore est Z = 17, donner le symbole complet
du noyau de Cl-36 ainsi que sa composition.
3617Cl
: 17 protons et 36-17 = 19 neutrons.
Le chlore 36 se désintègre en argon 36. Le numéro atomique de l'argon
36 est égal à 18.
Ecrire
l'équation de la désintégration et donner le type d'émission
radioactive obtenue.
3617Cl
--> 3618Ar
+ AZX.
Conservation du nombre de nucléons : 36 = 36 +A soit A = 0 ;
conservation de la charge : 17 = 18 + Z soit Z = -1.
3617Cl
--> 3618Ar
+ 0-1e. (radioactivité de type ß- )
|
Soit une bouteille d'eau minérale de 1,5 L. Le
nombre de noyaux de Cl-36 présents dans l'eau est égal à N = 2,4 108.
Quelle
est l'activité en Cl-36 de l'eau que contient cette bouteille ?
demi-vie t½ = 301 000 *365*24*3600 = 9,49 1012 s.
Constante radioactive l =
ln2 / t½= ln2 / 9,49 1012 =7,30 10-14 s-1.
Activité A = l N =7,30 10-14 * 2,4 108= 1,75 10-5 Bq.
En
déduire le nombre de désintégrations de noyaux de Cl-36 par jour.
1,75 10-5 *24*3600 =1,5.
|
On
veut dater une nappe d'eau souterraine à l'aide du chlore 36. On admet
que le nombre de noyaux de chlore 36 présents à l'instant t=0 de la
constitution de la nappe est égal au nombre de noyaux de chlore 36
présents dans un même volume d'eau de surface. Aujourd'hui l'eau ( non
renouvelée ) de la nappe d'eau souterraine ne contient plus que 38 % du
nombre de noyaux de chlore 36 trouvés dans les eaux de surface.
Déterminer
en années, l'âge de la nappe d'eau souterraine.
Loi de décroissance radioactive : N = N0 exp(-lt) ; ln ( N0 /N ) = lt ; t =ln ( N0 /N ) / l avec ln ( N0 /N )= ln (1/0,38)
=0,9676
et l = ln2 / 301 000 =2,3 10-6
an-1 ; t = 0,9676 / 2,3 10-6 =4,2 105
ans.
Le carbone 14 a une demi-vie de 5570 ans.
Pourquoi
ne l'a-t-on pas utilisé pour réaliser cette datation ?
Au delà de 7 à 8 demi-vie ( ~ 40 000 ans) , il ne reste pas
suffisamment de carbone 14 pour que la méthode de datation soit précise.
Jeu de flipper.
Un jeu de flipper est composé d'un plateau, d'un lance-billes, d'une
bille et de flippers proprement dits ( petits leviers actionnés
mécaniquement pour renvoyer la bille). Les premiers flippers n'avaient
pas de "flippers". Le problème concerne un flipper élémentaire
comprenant :
- le plateau carré de 50 cm de côté, incliné de 15° par rapport à
l'horizontale,
- le lance-bille, ressort terminé par deux rondelles, l'une sur
laquelle repose la bille, l'autre sur laquelle le joueur tire. La masse
du lance-bille est négligeable et on néglige les frottements. La
constante de raideur du ressort est k = 100 N m-1,
- la bille, de masse m = 50 g, placée au contact de la rondelle
supérieure.
Le joueur tire lentement sur la rondelle inférieure du lance-bille ( de
manière à garder la bille en contact de la languette supérieure ), et
racourci le ressort de 5 cm. Il lâche alors brusquement la rondelle
inférieure et la bille roule selon la ligne de plus grande pente du
plateau. On néglige le frottement de la bille sur le plateau et on
prend pour origine O, le point où se trouvait la bille au moment où
elle quitte le ressort du lanceur, définissant ainsi la " ligne de
lâcher".
Faire un
schéma du flipper en vue de dessus, en définissant le repère orthogonal
composé de l'axe de la trajectoire de la bille ( axe des y) et de la
ligne de "lâcher" ( axe des x).
Calculer
la distance maximale parcourue par la bille selon la ligne de plus
grande pente, avant de redescendre.
Système : bille + lanceur ; l'origine des énergies potentielles est
prise en O.
Initialement, date du lâcher, l'énergie mécanique est sous forme
potentielle EM = ½ky2 + mgz avec y = 0,05 m et z
= - y sin 15.
Au point le plus haut, la vitesse est nulle, l'énergie mécanique est
sous forme potentielle de pesanteur : EM = mg ymax
sin 15.
Au passage sur la ligne du lâcher en O, l'énergie mécanique est sous
forme cinétique : EM = ½mv2.
En absence de frottement, l'énergie mécanique se conserve : ½ky2
- mg y sin 15 =mg ymax sin 15.
ymax = ½ky2 / (mg sin 15)- y =0,5*100*0,052
/ (0,05*9,8*sin15) -0,05 =0,94 m.
En fait après que la bille ait parcouru 40 cm ( distance mesurée
entre l'origine du repère et le centre d'inertie de la bille ), elle
rencontre un obstacle correspondant à l'hypothénuse d'un triangle
rectangle isocèle placé dans le coin supérieur de façon à ce que sa
vitesse devienne horizontale sans changer de valeur.
Ecrire
l'équation de la trajectoire de la bille dans le repère Oxy.
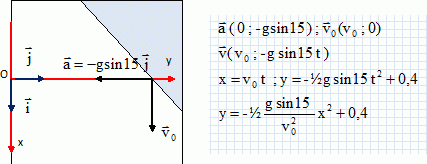
Calcul de v0 : ½ky2 - mg y sin 15 =½mv02
+ mg d sin 15 avec d = 0,40 m.
0,5*100*0,052 - 0,05*9,8*0,05 sin 15 = 0,5*0,05 v02
+0,05*0,40*9,8 sin 15
0,1186 = 0,025 v02 +0,051 ; v02
=2,71 ; v0 = 1,65 ~1,6 m/s.
y = -0,5 *9,8 *sin 15 / 2,71 x2+0,4.
y = -0,468 x2+0,4.
Calculer
la distance de l'origine à laquelle se trouve la bille lorsqu'elle
repasse la ligne de lâcher.
y =0 = -0,468 x2+0,4 ; x2 = 0,4/0,468 =0,855 ; x
= 0,92 m.
Circuit RLC.
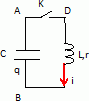
C = 0,2 µF ; L = 5 mH. La valeur de la résistance r peut varier. Soit
q(t) la charge du condensateur à l'instant t. A l(instant t=0, K est
fermé alors que le condensateur est porteur d'une charge q(0) non nulle.
Donner la
relation entre la tension uAB(t) et la charge
q(t) ; donner la relation entre q(t) et i(t) ; en dduire la relation
liant uAB(t) et i(t).
q(t) = C uBA(t) ; q(t) = -C uAB(t) ; i(t) =
dq(t) /dt = -CduAB(t) /dt.
Donner la
relation entre uBD(t) et i(t) ; en
déduire la realtion entre uBD(t) et q(t). déduire
l'équation différentielle à laquelle obéit q(t).
uDB(t) = Ldi/dt + ri ; uBD(t)
= -Ldi/dt - ri avec i = dq(t)/dt et di(t)/dt = d2q(t)
/ dt2.
uBD(t)
=-Ld2q(t) / dt2-rdq(t)/dt.
Additivité des tensions : uAB(t) + uBD(t)
+uDA(t) =0.
la tension aux bornes d'un interrupteur fermé est nulle : uDA(t).
-q / C -Ld2q(t)
/ dt2-rdq(t)/dt = 0 ; q / C +Ld2q(t)
/ dt2+ rdq(t)/dt = 0
d2q(t) / dt2 + 1/(LC) q(t)
+r/L dq(t)/dt = 0.Lorsque r=0, quelle est la
fréquence propre des oscillations du circuit ?
f = 1/(2p (LC)½) =
1/(6,28*(5 10-3*2 10-7)½) =5,0 103 Hz.
On note T la période associée à la fréquence propre du circuit.
Comment
se fait la répartition des énergies dans le circuit aux dates t =T et
t= 1,5 T ?
La solution de l'équation différentielle ( si r = 0) est de la forme
q(t) = q(0) cos ( 2pft).
A la date t=T, q(T) = q(0) cos(2 p ) =q(0) ; le
condensateur est chargé et stocke toute l'énergie du circuit ; la
bobine ne stocke pas d'énergie.
A la date t = 1,5 T, q(1,5T) =
q(0) cos p = -q(0) ;
le condensateur stocke toute l'énergie du circuit.
Si maintenant r est non nulle, pourquoi faut-il
apporter de l'énergie au circuit si l'on veut que les oscillations se
poursuivent indéfiniment ?
Lors des échanges d'énergie entre bobine et condensateur, une partie de
l'énergie du circuit se dissipe par effet Joule.
|
On introduit dans le
circuit un générateur de tension uAD= - ki ( k constante
positive ).
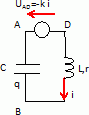
A quelle loi obéit
la charge q du condensateur ?
Additivité des tensions : uBA(t) + uAD(t)
+uDB(t) =0.
q/C -ki(t) +Ldi(t)/dt +r i(t) =0
i = dq(t)/dt ; di(t) /dt = d2q(t)
/ dt2.
q/C +(r-k)dq(t)/dt +Ld2q(t) / dt2= 0
A
quelle condition peut-il y avoir établissement d'oscillations
permanentes ?
Si r = k, l'équation différentielle s'écrit : q/C +Ld2q(t) / dt2= 0.
q(t) est sinusoïdale périodique.
|