Dipole
RC.
Un dipole RC peut être relié, en fermant l'interrupteur I, à un
générateur de tension continue E.
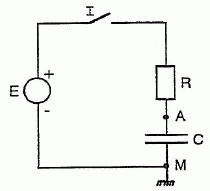
On donne R = 3 kW, C = 10 µF,
E = 5 V.
On mesure la différence de potentiel (VA-VM)
entre les points A et M ( masse). A l'instant t=0, on ferme
l'interrupteur I.
Au bout de combien
de temps le condensateur est-il chargé à 99% ?
Constante
de temps t = RC = 3000*10 10-6
=0,03 s.
Tension
aux bornes du condensateur en charge u = E(1-exp(-t/t).
0,99 E = E-E exp(-t/t) ; 0,01 = exp(-t/t) ; ln 0,01 = -t/t ; t = -t ln 0,01 =0,138~0,14 s.
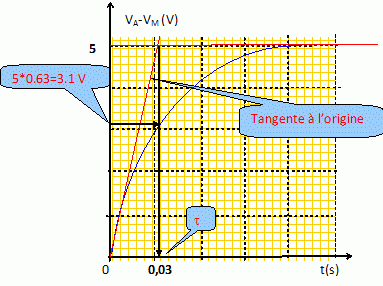
Représenter sur un
graphique l'allure approximative de la variation VA-VM.
Montrer commet déterminer graphiquement t.
|
Un
dipôle de nature inconnue est connecté à un générateur de tension
continue E. Au bout d'un certain temps le dipôle est traversé par un
courant d'intensité constante.
Peut-il
s'agir :
- d'une résistance.
Non, une résistance n'introduit pas de retard à l'établissement du
courant.
- d'une résistance en série
avec un condensateur. Non, l'intensité s'annule dès que le
condensateur est chargé.
- d'une bobine d'inductance
L en série avec une résistance R. Oui, la bobine inductive
introduit un retard à l'établissement du courant. En régime permanent,
l'intensité du courant est constante, non nulle.
|
Soit un dipôle RL
composé d'une bobine d'inductance L, de résistance négligeable, en
série avec une résistance R. Le dipôle peut être relié à un générateur
de tension continue E en fermant l'interrupteur I.
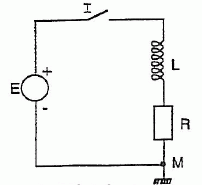
On donne R= 100 W, L=0,5 H et E = 5 V.
Comment
varie l'intensité i du courant dans le circuit lorsqu'on ferme
l'interrupteur ? Quel phénomène explique cette variation ?
La bobine inductive
introduit un retard à l'établissement du courant.
En régime permanent, l'intensité du courant est constante, non nulle.
i(t) = E/R
(1-exp(-t/ t)) avec t = L/R.
La bobine stocke de l'énergie ( ½Li2) , ce qui explique se
retard.
Ecrire la
relation algébrique entre R, L, E et i pendant la phase transitoire.
Additivité des tensions : E = Ldi/dt + ri.(1)
Calculer
la valeur de i pendant la phase transitoire.
Solution générale de Ldi/dt+Ri = 0 : i(t) = A exp(-t/t) avec t = L/R et A une constante.
Solution particulière de (1) en régime permanent i= E/R.
Solution générale de (1) : i(t) = A exp(-t/t) +E/R.
La continuité de l'énergie conduit à i(0) = 0 soit 0 = A +E/R d'où A =
-E/R.
i(t) = E/R (1-exp(-t/ t)).
Calculer
la constante de temps.
t = L/R = 0,5 / 100 = 5 10-3
s = 5 ms.
Calculer
l'énergie stockée dans la bobine.
½LI2 avec I = E/R =5/100 = 0,05 A.
½LI2 =
0,5*0,5*0,052 =6,25 10-4 J.
Soit le circuit suivant comportant un condensateur de capacité C = 0,1
µF, une résistance R, une bobine d'inductance L =0,1 H de résistance r
et un générateur de tension continue E.
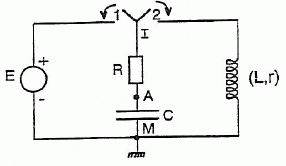
On place l'interrupteur en position 1 et le condensateur se charge
complètement. On bascule l'interrupteur en position 2.
A partir
de cet instant, comment varie la tension uAM aux bornes du condensateur en
supposant les valeurs de R et r très faibles ?
Le régime est pseudopériodique faiblement amorti. La tension aux bornes
du condensateur est pratiquement sinusoïdale.
Calculer
la période propre du dipôle LC correspondant.
T = 2 p(LC)½
=6,28 (0,1*0,1 10-6)½ =6,28 10-4 ~6,3
10-4 s.
Tremplin de saut à ski.
Un
tremplin de saut à skis comprend une piste d'élan de profil curviligne
prolongée par une piste de réception plane et inclinée par rapport à
l'horizontale d'un angle a.
Le skieur est assimilé à un point matériel noté G. On négligera les
frottements. La trajectoire du skieur est contenue dans un plan
vertical.
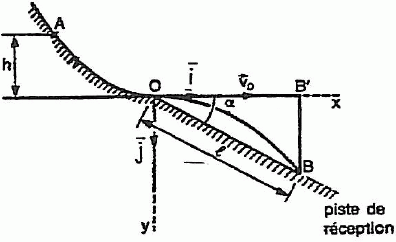
Le
skieur part du point A sans vitesse initiale, perd contact avec la
piste curviligne au point O. Sa vitesse à cet instant est horizontale
et est notée v0.
Faire le bilan des forces extérieures appliquées au skieur sur la partie OA de la trajectoire.
Le skieur est soumis à son poids, vertical, vers le bas, valeur mg et à l'action du plan, perpendiculaire au plan.
Enoncer
le théorème de l'énergie cinétique et établir l'expression
littérale relaint l'altitude h du point a par rapport à O et la
vitesse v0 en O.
La variation de l'énergie cinétique est égale à la somme des travaux des forces appliquées au skieur entre A et O.
L'énergie cinétique est nulle en A et vaut ½mv02 en O.
Le travail du poids est moteur en descente et vaut : mgh.
L'action du plan perpendiculaire à la vitesse ne travaille pas.
½mv02 -0 = mgh ; ½v02 = gh.
A.N : h = 10 m ; g = 10 m s-2 ; v0 = (2gh)½ =(200)½ =14,14 ~14 m/s.
Dans le repère (O i j ) montrer que l'équation de la trajectoire aérienne de G s'écrit : y = gx2 / (2 v02).
Le skieur n'est soumis qu'à son poids : la chute est libre.
Dans le repère ( O i j ) : composantes de l'accélération : (0 ; g ) ; composante de la vitesse initiale ( v0 ; 0 ) ; position initiale (0 ; 0 ).
La vitesse est une primitive de l'accélération : composantes de la vitesse : ( v0 ; gt)
La position est une primitive de la vitesse : x = v0t ; y = ½gt2.
t = x/v0 ; repport dans y : y = gx2 / (2 v02).
|
Au point B le skieur reprend contact avec la piste de réception.
Etablir l'expression des coordonnées xB et yB du point B en fonction de v0, a et g.
Equation de la portion de droite OB : y = tan a x.
Au point B : tan a xB = gxB2 / (2 v02).
tan a = gxB / (2 v02) ; xB =2 v02 tan a / g ; yB = tan a xB =2 v02 tan2 a / g.
A.N : a = 45 °.
xB =2 *200*tan 45 / 10 = 40 m ; yB = tan 45 * 40 = 40 m.
En déduire la longueur du saut L= OB.
OB2 = xB2 + yB2 =402+402 = 3200 ; OB =56,57 ~57 m.
Calculer la durée du saut.
xB = v0t ; t = xB / v0 = 40 / 14,14 = 2,8 s.
|
|




