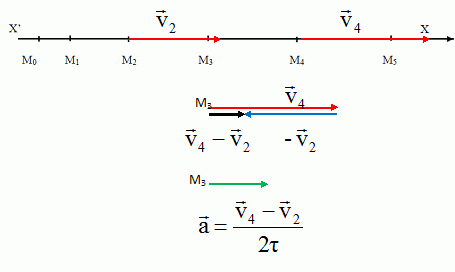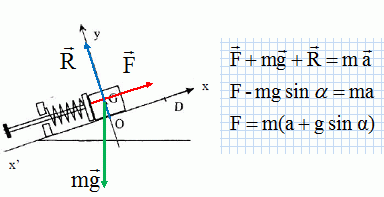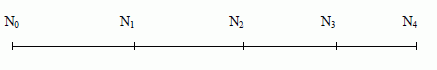Un
solide en acier de masse m = 30,0 g peut se déplacer sur un plan
incliné d'un angle α = 35,0° avec l'horizontale. En D, le solide passe
avec une vitesse VD acquise à l'aide d'un ressort.
On peut considérer les frottements comme négligeables dans cette
partie, lorsque le solide glisse sur le plan.
Intensité du champ de pesanteur au niveau du sol : g = 9,80 m.s-2.
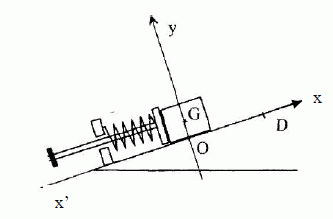
La
position du centre d'inertie G du solide est repérée sur un axe x'x de
même direction que la ligne de plus grande pente du plan incliné et
orienté vers le haut.
|
On
tire sur la tige et on comprime ainsi le ressort jusqu'à ce que le
centre d'inertie du solide se trouve au point O, puis on lâche la tige.
Lorsque le centre d'inertie du solide arrive en D, le ressort est
bloqué et le solide
est libéré.
La figure suivante représente à l’échelle 1 les positions occupées par
le centre d'inertie G du solide pendant la phase de propulsion à des
intervalles de temps réguliers τ = 40,0 ms (points M0 à M5).
A t = 0 le centre d'inertie du solide est au point O ou MO.
|

Déterminer
à 10-3 près les vitesses V2 et V4 du solide aux
points M2 et M4 en effectuant des
mesures sur la figure.
V2 = (M1M2 + M2M3)
/ (2t) =(3,2 + 4,3) 10-2
/ (2*0,040) =0,9375 ~0,938 m s-1.
V4 = (M3M4 + M4M5)
/ (2t) =(4,8 + 5,1) 10-2
/ (2*0,040) =1,2375 ~1,24 m s-1.
Exprimer
le vecteur accélération a du solide au
passage du point M3 en fonction des
vitesses V2 et V4 et de l’intervalle
de temps τ.
En
déduire la valeur de cette accélération a.
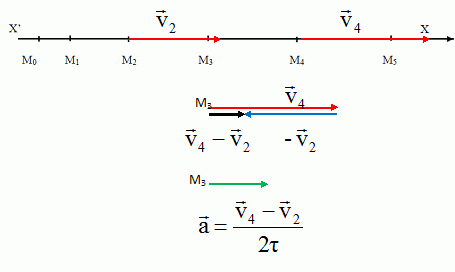
a = (1,2375-0,9375) / (2*0,040) =3,75 m s-2.
Représenter
les forces qui s'appliquent au solide sur un schéma.
En
appliquant la seconde loi de Newton au solide exprimer la valeur de la
force de rappel F du ressort en fonction de m, g, α et de
l’accélération a.
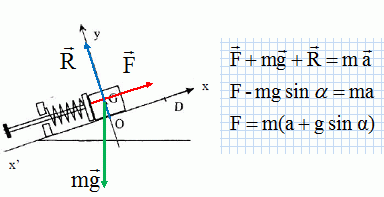
Calculer
à 10-2 près la valeur de F
au point M3.
F = 0,030(3,75+9,8 sin 35) = 0,28 N.
En D la vitesse du
solide est VD = 2,00 m.s-1. Il glisse ensuite
jusqu'au point E où il s'arrête.
Dans cette partie du mouvement, on prendra la position du centre
d'inertie du solide en D comme origine des altitudes (ZD =
0) et comme niveau de référence de l'énergie potentielle de pesanteur :
EPP(D)=0.
Représenter
sur un schéma les forces qui s'appliquent au solide sur le trajet DE.
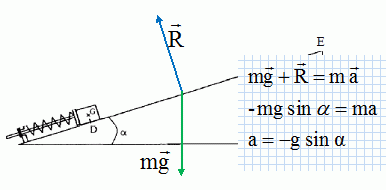
Donner
l'expression au point D de l'énergie mécanique Em(D) du
solide en translation dans le champ de pesanteur.
L'énergie mécanique est la somme de l'énergie cinétique et de l'énergie
potentielle.
Em(D) = ½mv2D+mgZD
avec ZD
=0 ; Em(D) = ½mv2D.
Donner l'expression
de l'énergie mécanique Em(E) du solide au point E, en
fonction de m, g, α et de la distance DE.
Em(E) = ½mv2E+mgZE
avec VE
=0 ; Em(E) = mgZE = mg
DE sin a.
En
admettant que l'énergie mécanique du solide en translation dans le
champ de pesanteur se conserve, calculer la valeur de la distance DE.
Em(D) =Em(E) ; ½mv2D =mg DE sin a ; DE =v2D /(2gsin a )=4/(2*9,8*sin35)=0,3558 ~0,356 m.
La
figure suivante représente à l’échelle ½ les positions occupées
par le centre d'inertie G du solide à des intervalles de temps
réguliers τ’ = 40,0 ms (points N0 à N4). A t = 0,
le centre d'inertie du solide est au point D ou N0.
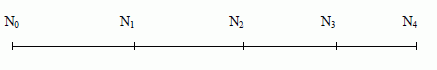
Vérifier que les
espaces successifs parcourus par G : N0N1, N1N2, N2N3 et N3N4 sont en progression
arithmétique de raison r = -9,10-3 m,
approximativement.
N0N1=0,112 m ; N1N2 =0,103 m ; N2N3 =0,094 m ; N3N4 =0,085 m ;
N1N2 =N0N1-9 10-3 m ; N2N3 =N1N2-9 10-3 m ; N3N4 =N2N3-9 10-3
m.
Etablir
l’équation du mouvement en prenant D comme origine des espaces et le
passage en D comme origine des temps.
Le mouvement s'effectue suivant l'axe x'x ; on note a l'accélération.
La vitesse est une primitive de l'accélération : v = at+ constante
à t=0, v = vD = 2,00 m/s d'où la valeur de la constante :
constante = vD = 2,00 m/s.
La position est une primitive de la vitesse :
x = ½at2 + VDt + Cste.
à t=0 le solide est en D, origine des espaces : Cste = 0.
x = ½at2 + VDt ; x = ½at2 + 2t.
Etablir
l’expression de r en fonction de g, α et τ’. En déduire la valeur de
l’accélération du solide sur la trajectoire DE à 10-2 près.
N0N1=0,5 at'2 + 2t' ; N0N2 =0,5 a(2t')2+2*2t' ; N0N2 =2 at'2+4t' ;
N0N2 =N0N1 +N1N2 =N0N1 +N0N1 + r ; 2 at'2+4t' = at'2
+ 4t' +r ; at'2=
+r.
de plus a = - g sin a d'où r = -g sin a t'2.
a = r / t'2
= 9 10-3 / 0,042 =5,62~ -6 ms-2.
|
En
E, le solide subit une chute verticale sans vitesse initiale dans une
éprouvette contenant un
liquide. On admettra que dans ce cas, le solide est soumis à une force de frottement fluide,
représentée par un vecteur f de même direction que le
vecteur vitesse V mais
de sens opposé et de valeur f=kV, k étant une constante positive.
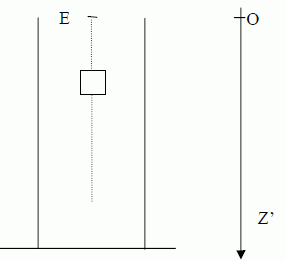
Faire l'inventaire
des forces qui s'appliquent sur le solide pendant sa chute dans le
liquide et les représenter sur un schéma.
Le solide est soumis à son poids, à la poussée d'Archimède et à la
force de frottement fluide.
En
appliquant la seconde loi de Newton, montrer que le mouvement du centre
d'inertie du solide obéit à une équation différentielle du type
dV/dt = α − β.V.
Donner
les expressions littérales de α et β en fonction des données du texte,
de la masse volumique ρ du liquide et du volume VS du
solide.
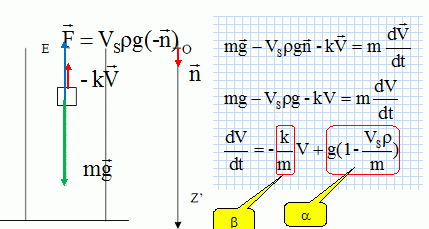
En
utilisant le graphe V=f(t) de la figure suivante, calculer
numériquement les valeurs de α et β en justifiant votre démarche.
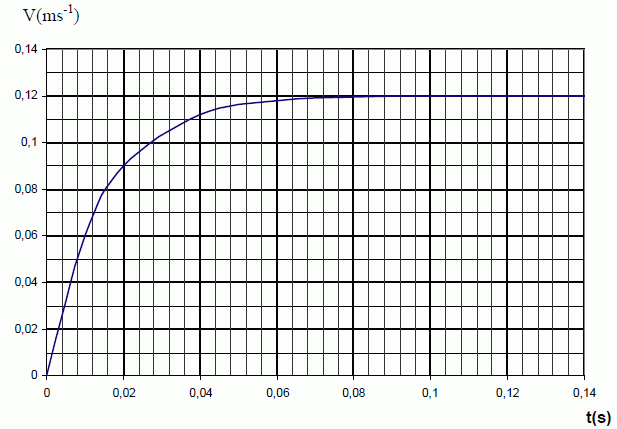
Lorsque la vitesse limite Vlim est
atteinte dVlim /dt = 0 ( mouvement rectiligne uniforme)
d'où Vlim = a/b.
Lecture graphe Vlim =0,12 m s-1 ;
a = 0,12 b.
[dV/dt
]0= α − β.V(t=0) avec V(t=0)
=0.
Le coefficient directeur de la tangente à l'origine est égal à a.
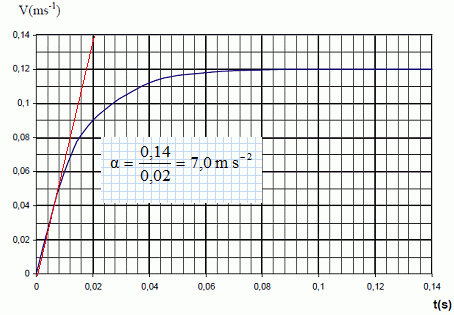
b = a / 0,12 = 7,0 / 0,12 = 58,33 ~58 s-1.
|