Dualité
onde-corpuscule.
Donner les
caractéristiques d'une onde électromagnétique.
Les ondes électromagnétiques se propagent en ligne
droite dans un milieu homogène et isolant, y compris le vide.
Dans le vide ( ou dans l'air), leur célérité vaut : c = 3,0.108
m.s-1 . Dans un câble coaxial ( fibre
de verre ), elle vaut »
2,0.108 m.s-1 .
Elles tranportent de l'énergie et sont sont caractérisées par
leur fréquence v.
Qu'est ce qu'un
photon ? Quelles sont ces caractéristiques ?
Les photons sont des « paquets »
d’énergie élémentaires échangés lors de l’absorption ou de l’émission
de lumière par la matière.
Le photon est une particule de masse nulle, de spin égal à 1.
L'énergie du photon est liée à sa fréquence caractéristique : E = h v.
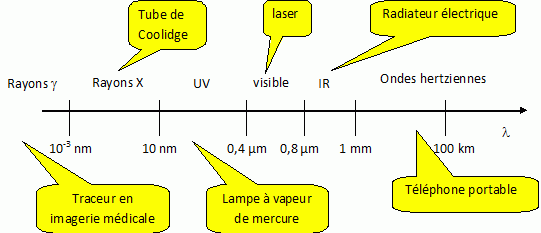
|
La station France
Inter émet en modulation d'amplitude sur la fréquence f = 164 kHz.
Pourquoi
qualifie t-on France Inter d'émetteur "grandes ondes" ?
l = c / f = 3 108 /
1,64 105 = 1829 m.
On appelle grandes ondes (GO) ou ondes tongues (OL), la bande de
radiofréquences qui s'étend
de 30 kHz a 300 kHz.
|
Calculer en J et en
eV, l'énergie des photons de fréquence respective 5,00 1017
Hz et 2,83 1013 Hz.
E = h v
= 6,63 10-34 *5,00 1017
=3,32 10-16 J ;
3,32 10-16
/ 1,6 10-19 =2,07 103 eV ; l = c / v = 3 108 / 5,00 1017 = 6,00 10-10 m = 0,600 nm ( rayon g ).
E2 =6,63
10-34 *2,83 1013 =1,88 10-20
J ;
1,88 10-20 / 1,6 10-19
=0,117 eV ; l = c / v = 3 108 / 2,83 1013 = 1,06 10-5 m = 10,6 µm ( IR ).
Le rayonnement le plus dangereux possède la plus grande fréquence.( rayon g
). Comme les rayons X, les rayons g
sont dits "ionisants" : ils peuvent arracher des électrons à la matière
vivante.
Dans les lycées, on utilise des lasers qui sont dangereux pour l'oeil.
Etude
d'un réseau.
Considérons
un réseau par transmission de pas a, que nous supposerons infiniment
fines et parallèles, éclairé par un faisceau de lumière parallèle,
monochromatique de longueur d'onde l,
sous une incidence i0.
l'angle de diffraction est noté i'.
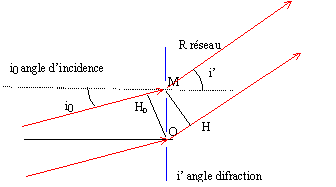
Exprimer
la différence de marche d
entre deux rayons homologues séparés par une distance a dans le plan du
réseau.
La différence de chemin optique entre le
rayon passant par le point O et celui passant par le point homologue M
vaut ( l'indice de l'air vaut 1) : OM = a
d =OH-MH0 =
a sin i'- a sin i0 = a( sini'-sin i0) avec a =
1/n ; n pas du réseau en nombre de traits par mètre.
Le interférences sont constructives
entre les ondes diffractées si la différence de marche d est un multiple de la longueur d'onde l.
a( sini'-sin i0) = kl avec k entier positif,
nul ou négatif
sin i'-sin i0 = kl n.
Un réseau de 500 traits par millimètre est utilisé sous incidence
normale avec une source de longueur d'onde l = 600 nm.
Déterminer
les ordres observables et calculer les positions des maxima principaux.
i0 = 0 ; sin i0 = 0 ; n = 500 *1000 = 5 105
traits par mètre : l n = 600
10-9 *5 105 = 0,3
sin i' = 0,3 k ; k = 0 : i = 0
k = 1 : sin i' = 0,3 : i' = 17,5 ° ; k=-1 : i' = -17,5 °
k = 2 : sin i' = 0,6 : i' = 36,9 ° ; k=-1 : i' = -36,9 °
k = 3 : sin i' = 0,9 : i' = 64,2 ° ; k=-1 : i' = -64,2 °.
Observation du spectre de la
lumière blanche.
Le réseau précédent
reçoit un faisceau de lumière blanche de longueurs d'onde : 0,400
µm < l < 0,800 µm.
On étudie le spectre diffracté d'ordre 1. Le faisceau émergent est
recueilli sur un écran, dans le plan focal image d'une lentille
convergente de distance focale f' = 1,0 m.
Quel doit
être l'angle d'incidence i pour que le faisceau de longueur
d'onde moyenne lmoy
= 0,600 µm converge en F', foyer principal image de la lentille ?
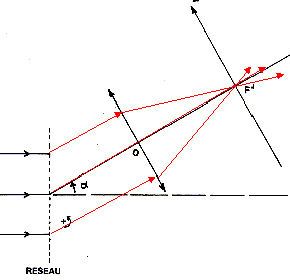
sin i0 = 0 et k=1 ; sin
i' = l n.
Un rayon incident parallèle à l'axe
optique principal de la lentille émerge en passant par le foyer
principal image F' : donc i' = a ;
sin a = lmoy n = 0,6 10-6 *5 105 = 0,3 ; a =17,5 °.
Déterminer
les distances entre F' et les raies associées aux radiations extrèmes
du spectre.
Pour une longueur d'onde l, voisine de lmoy (l
< lmoy ), on obtient une
image en un point d'abscisse x (x petit devant f') dans le plan focal
de la lentille.
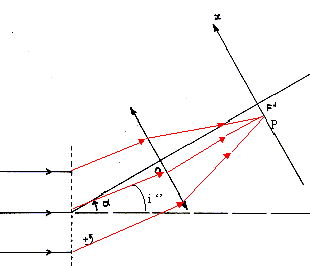
x = f'.n.(l - l0
)/ cosa. (voir
ci-dessous)
Pour le bleu : xB =1*5 105(400-600) 10-9
/ cos17,5= -0,10 m.
Pour le rouge : xR =1*5 105(800-600)
10-9 / cos17,5= +0,10 m.
Justifier
l'expression suivante : a cos i'k di' = kdl pour i0 fixé.
Lorsque deux ondes planes, de longueurs d'ondes voisine l et l +dl, tombent
sur un réseau en faisant le même angle d'incidence i0,
l'écart di entre les angles que font les ondes diffractées, s'obtient
en différentiant l'équation :
sin i'-sin i0 = kl
n ;
cos i'k di'= kn dl ; di'/ dl = kn /cos i'.
Lorsque i'k est proche de
zéro, cos i'k ~ 1 : di'= kn dl.
Dx étant la distance dans le plan
focal image de la lentille entre deux raies de longueurs d'onde
voisines,
démontrer
que pour i'k est proche de zéro,
Dx = a
Dl.
Exprimer a en fonction de k,
f' et a.
l <l0 ; sin i'' = nl ; sin a = nl0
; donc i'' <a.
tan(a-i") = x/ f '~ (a-i")
radian ; x = f '(a-i") = f 'di'
or di' = n dl /cos a pour k= 1
x= f ' n dl /cos a = f n (l0-l) /cos a
x = f.n.(l - l0
)/ cosa.
|
Spectre de
Fraunhofer.
Le soleil est une étoile moyennement
chaude en surface, la couleur perçue est jaune.
La
longueur d'onde à laquelle le rayonnement est le plus intense, à une
température précise est donnée par la loi de Wien : lmax lmax= k/T
T : température en kelvin de la source ; k = 2,9 10-3 mK =
constante.
En déduire la
température de surface du soleil ( lmax=
500 nm)
T = 2,9 10-3 / 500 10-9
=5800 = 5,8 103 K.
Les étoiles Rigel et Bételgeuse sont des étoiles respectivement bleue
et rouge.
Classer ces étoiles
par ordre croissant de leur température de surface.
lbleu=
400 nm ; TRigel = 2,9 10-3 / 400 10-9
=7250 = 7,3 103 K.
lrouge=
700 nm ; TBételgeuse = 2,9 10-3 / 700 10-9
=4140 = 4,1 103 K.
Bételgeuse, Soleil, Rigel.
On visualise le spectre de la lumière provenant du soleil. Il s'agit
d'un spectre présentant un fond coloré sur lequel apparaissent quelques
raies noires.
Quel est ce type de
spectre ?
Spectre de raies d'absorption.
La couronne solaire contient des éléments chimiques qui absorbent
certaines radiations de la lumière blanche émise par l'astre central.
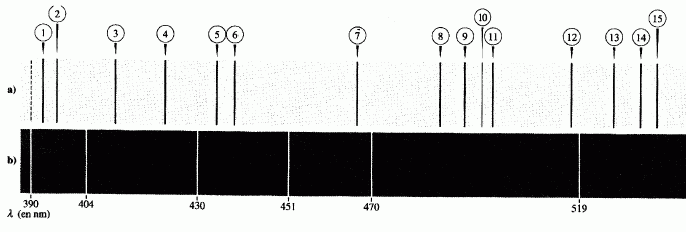
Le
document ci-dessus représente un extrait du spectre du soleil ( les
principales raies noires sont repérées par un numéro ).On dispose
également d'un extrait du spectre d'émission de l'argon obtenu
dans
les mêmes conditions.
Utiliser la raie d'émission de 390 nm comme référence.
Déterminer les
longueurs d'onde des raies noires observées dans le spectre du soleil.
On mesure les distances L ( mm) entre la raie d'émission de 390 nm et
les autres raies d'émission.
l (nm)
|
390
|
404
|
430
|
451
|
470
|
519
|
545
|
L
(mm)
|
0
|
17
|
51
|
79
|
104
|
169
|
204
|
On mesure les
distances L ( mm) entre la raie d'émission de 390 nm et les autres
raies d'absorbtion du soleil.
n°
|
1
|
2
|
3
|
4
|
5
|
6
|
7
|
8
|
9
|
10
|
11
|
12
|
13
|
14
|
15
|
L(mm)
|
3,5
|
8
|
26
|
41
|
57
|
62
|
100
|
125
|
133
|
138
|
142
|
166
|
179
|
187
|
192
|
| l (nm) |
402
|
405
|
416
|
429
|
442
|
445
|
474
|
495
|
500
|
504
|
506
|
526
|
534
|
541
|
546
|
élément
|
|
|
|
|
|
|
|
Fe
|
|
|
Ni
|
Ca
|
Fe
|
Fe
|
|
|
|




