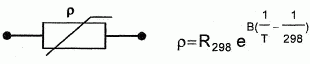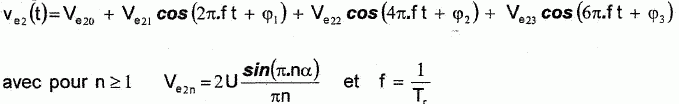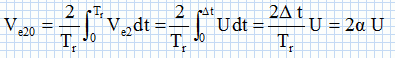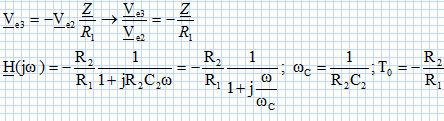Le capteur.( de type résistance CTN)
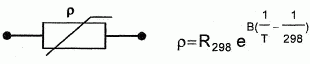
T est la température exprimée en Kelvin ; R298 = 22 kW et B = 4200 K-1.
On donne la relation permettant de convertir des températures exprimées en kelvins, en degrés Celsius : T(K) = q(°C) + 273,15.
Que signifie le sigle CTN ? Coefficient de température négatif.
Ce capteur est-il linéaire ?
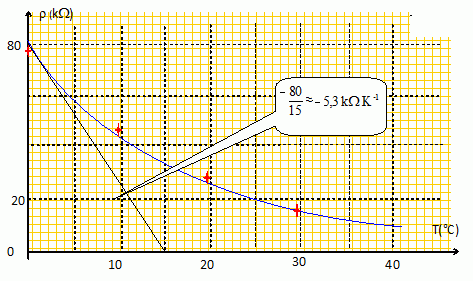
Non, r n'est pas une fonction affine de T ( voir graphe ci-dessous).
Citer au moins deux autres capteurs de température.
Thermocouples, sonde de platine PT100, la CTP, coefficient de température positif (PTC
thermistor).
Calculer la résistance r à la température de 30°C.
T = 30+273,15 = 303,15 K , 1/303,15 -1/298 = (298-303,15) / (298*303,15) = -5,7 10-5 ; -5,7 10-5 *4200 = -0,2394.
r = 22 exp (-0,2394) = 17,3 ~ 17 kW.
Déterminer graphiquement la sensibilité de la CTN au voisinage de 0°C.
Tracer la tangente à l'origine et déterminer son coefficient directeur.
Par contre, au voisinage de 100 °C, la tangente est pratiquement
horizontale : son coefficient directeur est proche de zéro et la
sensibilité de la CTN est voisine de zéro.
On souhaite vérifier le relevé de la caractéristique de la résistance en fonction de la température.
Proposer un schéma de montage.
On désire tracer la courbe R= f(q) ; la CTN doit plonger dans un bain marie dont on relevera la température. Celle-ci variera de 5 °C en 5 °C.
La sonde du thermomètre doit être attachée avec du scotch à la CTN ; agiter la solution du bain.
Relier la CTN à un ohmmètre. Conditionnement de la température.
On utilise un montage diviseurde tension, c'est à dire que l'on met en
série le capteur avec une résistance R. Deux possibilités sont
représentées ci-dessous :
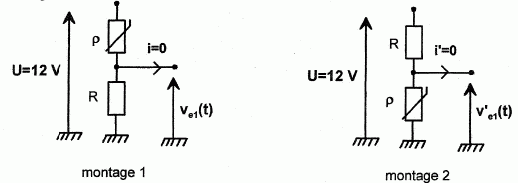
Pour chaque montage, donner l'expression de V'e1 et de Ve1 en fonction de R, r et U.
On note I l'intensité qui traverse le capteur et la résistance R : Ve1=R I ; U = (R+r) I ; Ve1=R U /(R+r)
V'e1= r I ; U = (R+r) I ; V'e1=r U /(R+r).
On souhaite que le montage à utiliser puisse fournir une tension qui augmente lorsque la température augmente.
Quel montage choisir ? Justifier.
Ve1=R U /(R+r) = U / (1+r/R).
r diminue si la température augmente ; (1+r/R) diminue donc si la température augmente et en conséquence U / (1+r/R) augmente avec la température. ( montage 1)
Pour une température de 50°C, le capteur a une résistance r = 7390 W.
En utilisant le montage 1, calculer R si Ve1 = 5 V à cette température.
5 = 12 R /(7390+R) ; 5 (7390+R) = 12 R ; 5 R + 5*7390 = 12 R ; 7 R = 5*7390 ; r = 5*7390 / 7 =5,3 kW.
Transmission de la température.
On admet que Ve1 = g q avec g = 3,85 10-2 V °C-1.
Le transmetteur est représenté dans son principe sur la figure
ci-dessous. L'amplificateur opérationnel fonctionne en commutation,
c'est à dire :
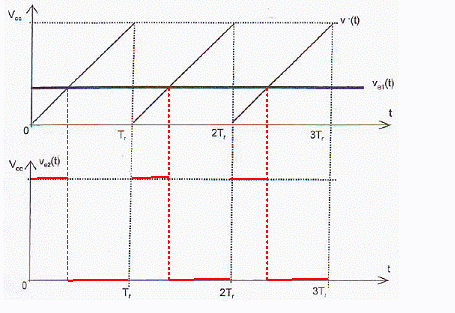
Si V+ > V-, on a Ve2 = VCC = 5 V.
Si V+ < V-, on a Ve2 =0.
Sur l'entrée inverseuse, on applique une tension en dents de scie qui a pour expression V-(t) = VCC / Tr t dans l'intervalle [0 ; Tr].
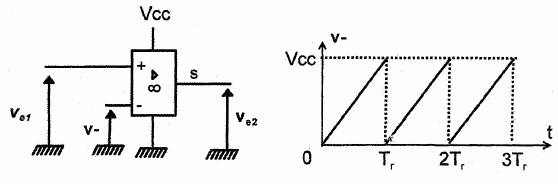
Ve1-V- =g q -VCC / Tr t.
Si g q -VCC / Tr t >0, alors Ve2 = VCC.
Si g q -VCC / Tr t <0, alors Ve2 = 0.
Dans l'intervalle [0 ; Tr], la durée Dt pendant laquelle Ve2 = VCC est égale à :
g q -VCC / Tr Dt >0 ; g q >VCC / Tr Dt ; g q Tr / VCC > Dt ;
on pose ß =g Tr / VCC ; par suite Dt < ß q.
Récupération de l'information.
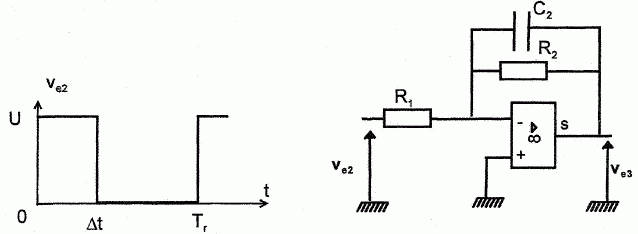
Après avoir été transmis, le signal contenant l'information température est récupéré par le dispositif suivant.
On admet donc que la lageur d'impulsion Dt reste proportionnelle à la température mesurée selon Dt = ß q avec ß = 7,7 10-5 s °C-1.
On appelle a = Dt / Tr avec Tr = 10 ms et U = 5 V.
La tension Ve2 est périodique et peut s'écrire comme une somme de fonctions sinusoïdales comportant 4 termes :
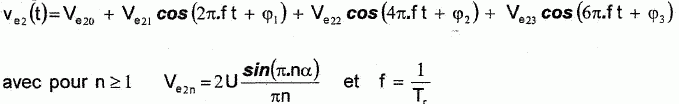
Que représente le terme Ve20 ?
Ve20 représente deux fois la valeur moyenne de Ve2.
Déterminer Ve20 en fonction de Dt, Tr et U.
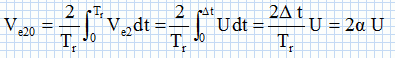
Pour la suite du problème, on prendra q = 80 °C.
Calculer a et Ve20.
Dt = ß q = 7,7 10-5 *80 = 6,16 10-3 s = 6,16 ms
a = Dt / Tr = 6,16 /10 = 0,616 ~0,62.
Ve20 = 2 a U = 2*0,616 *5 = 6,16 ~6,2 V.
Calculer Ve21. n= 1.
Ve21 = 2*5 sin(0,616 *3,14) / 3,14 = 2,97 ~3,0 V.
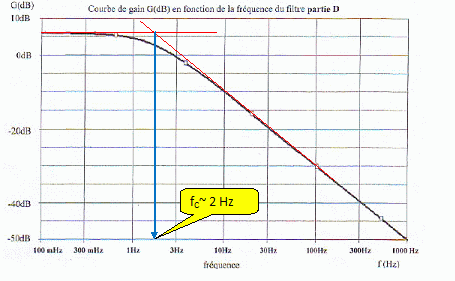
Préciser qualitativement le type et l'ordre du filtre ci-dessus.
Filtre passe bas d'ordre 1.
Exprimer alors la transmittance complexe T(jw) = Ve3 / Ve2.
C2 et R2 sont en dérivation : admittance complexe Y = jC2w +1/R2 = ( jR2C2w +1) /R2 .
Impédance complexe Z = 1/Y = R2 /( jR2C2w +1).
Ve3 +Z i =0 ; Ve2 = R1 i.
Ve3 +Z Ve2 / R1= 0
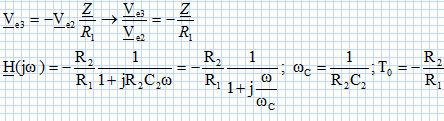
On pose x = w / wC ; H =-T0 / (1+jx) =-T0 (1-jx)/ (1+x2) ; Module de H : H = T0 (1+x2)-½.
Gain en dB : G = 20 log H = 20 log T0 -10 log(1+x2)
Quand la fréquence tend vers zéro, ( x tend vers zéro ) le gain tend vers 6 dB.
Quand la fréquence devient grande, H tend vers zéro et le gain tend vers zéro.
H(100) = T0 (1+502)-½= 0,02 T0.
Amplification : A =| Ve3 / Ve2| ; G(dB) = 20 log A ou A = 10 G/20.
A( f-->0) = 10 6/20 = 2 ; A( f=100) = 10 -30/20 = 0,03.
|
Commande du chauffage et sécurité.
Il est réalisé à l'aide d'un montage à transistor.
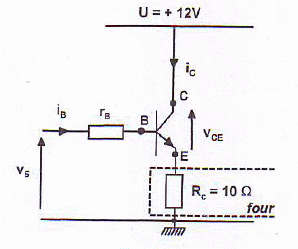
Le transistor fonctionne en commutation ; le gain en courant ß =IC / IB, sera supposé grand.
V5 >0, iB est grand, le transistor est saturé iC est différent de zéro) et VCE sat = 0,8 V.
V5 =0, iB =0, T est bloqué et IC=0.
Lorsque V5 >0, exprimer le courant IC.
RCIC + VCE sat = U ; IC =( U-VCE sat ) / RC= (12-0,8) / 10 = 1,12 A~ 1,1 A.
Calculer la puissance du four.
P = RC I2C = 10*1,122 =12,54 W ~ 13 W.
Calculer l'énergie fournie au four en 10 min.
W = P Dt = 12,54 * 10*60 = 7526 J ~ 7,6 kJ.
Que signifient les symboles suivants ?

CE : marquage européen pour les produits soumis à une ou plusieurs directives européennes.
NF : marquage de certification, norme française.
Appareils de classe 2 ( double isolation ). Les masses ne sont pas reliées à la terre.
|
|