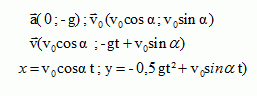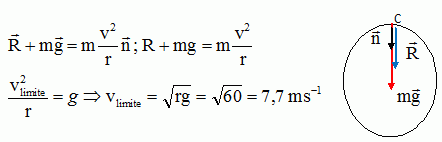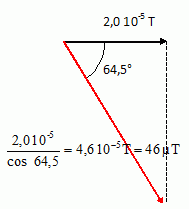Pendule, projectile, tube néon, solénoïde, champ magnétique terrestre , concours kine.

QCM n°1. Un mobile se déplace sur un axe Ox ; on note "a" son accélération et "x", son abscisse. On donne  a = -4x ; abscisse initiale x0 =0,20 m ; vitesse initiale v0 = 0. Quelle(s) la (les) proposition(s) exacte(s) ? A. Le mouvement est rectiligne uniformément varié. Faux. Dans un mouvement rectiligne uniformément varié, le vecteur accélération est constant. B. L'équation horaire du mouvement est : x(t) = 0,2 cos ( 4t+p). Faux. x' = 0,2 *(-4) sin ( 4t+p) ; x" = a = 0,2 (-4)*4 cos ( 4t+p) = -16 x C. L'équation horaire du mouvement est : x(t) = 0,2 cos ( 4t). Faux. x' = 0,2 *(-4) sin ( 4t+p) ; x" = a = 0,2 (-4)*4 cos ( 4t+p) = -16 x D. L'équation horaire du mouvement est : x(t) = 0,2 cos ( 2t). Vrai. x' = 0,2 *(-2) sin ( 2t) ; x" = a = 0,2 (-2)*2 cos ( 2t) = -4 x. E. Il est impossible de daractérisé le mouvement. Faux. QCM n°2. Un pendule, de longueur L, est écarté d'un angle q0 avec l'horizontale ; il est lancé avec une vitesse initiale v0. 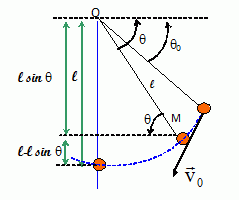Quelle est la  relation donnant la vitesse de la bille ? La bille est soumise  à son poids et à la tension du fil. La tension, perpendiculaire  à la vitesse, ne travaille pas. Travail du poids en passant de la position initiale  à M : la position la plus basse est choisie comme origine des altitudes. Altitude initiale : L - L sin q0 ; altitude en M : L - L sin q ; le travail du poids est moteur en descente. W(poids) = mg( L sin q -L sin q0 ) Variation de l'énergie cinétique de la bille de masse m : ½mv2-½mv02 ; théorème de l'énergie cinétique : ½mv2-½mv02 =mg( L sin q -L sin q0 ) v2= v02 +2gL(sin q -sin q0) ; v = [v02 +2gL(sin q -sin q0)]½. QCM n°3, 4, 5. La bille doit pénétrer dans le tube de diamètre légèerement supérieur à celui de la bille. 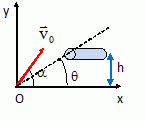a = 30 ° ; g = 10 m s-2 ; h = 125 cm. Quelle est la valeur de la vitesse de la bille lorsqu'elle pénètre dans le tube ? La bille pénètre dans le tube si, à l'entrée du tube, la vitesse est horizontale. 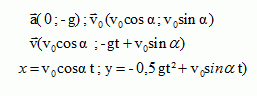v = v0 cos 30 ; -10 t + v0 sin 30 = 0 ; 10 t = v0 sin 30 =0,5 v0. y = h = 1,25 = -5 t2 +v0 sin 30 t = -5 t2 +10 t2 = 5 t2 ; t = 0,5 s Par suite v0 = 20 t = 10 m/s et v = 10 cos 30 = 8,7 m s-1.   A quel instant la bille pénètre t-elle dans le tube ? t = 0,5 s. Quel est la valeur de l'angle q ?  A l'entrée du tube : tan q  = y / x  ;  y = 5 *0,52 = 1,25 m ; x = 10 cos 30 * 0,5 =4,33 m ;  tan q  =1,25 / 4,33 = 0,2886 ; q = 16,1 °. QCM n°6, 7, 8. Le manège simule les montagnes russes sur lesquelles se déplace une voiture sous l'action de son poids. La voiture est assimilée  à un point matériel M de masse m glissant sans frottement sur son support. On néglige la résistance de l'air. h = 18 m ; r = 6 m ; g = 10 m s-2. 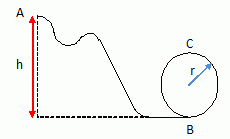Calculer la vitesse de la voiture en B ( la vitesse en A est 1 m/s). Travail moteur du poids en descente : mgh ; l'action du support perpendiculaire  à la vitesse ne travaille pas. Variation de l'énergie cinétique : ½mvB2 - ½mvA2. Théorème de l'énergie cinétique : ½mvB2 - ½mvA2= mgh vB2 = vA2+ 2 gh ; vB = (vA2+ 2 gh)½ =( 1 + 20*18)½ =  19 m/s. La boucle circulaire décrite par la voiture se trouve dans un plan vertical. Quelle est la vitesse minimale en C pour que la voiture reste en contact avec la piste ? En C l'action du support ne doit pas être nulle, sinon c'est la chute. 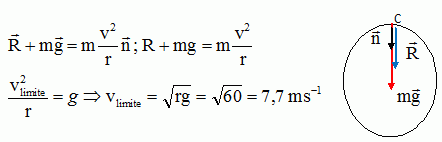Quelle doit être la hauteur  minimale hmini pour que la voiture fasse un tour complet en restant en contact avec la piste ? Travail moteur du poids en descente entre A et C : mg(hmini -12) ; l'action du support perpendiculaire  à la vitesse ne travaille pas. Variation de l'énergie cinétique : ½mvC2 - ½mvA2. Théorème de l'énergie cinétique : ½mvC2 - ½mvA2= mg(hmini -12) vC2 - vA2= 2 g(hmini -12) ; hmini  = 12 + (vC2 - vA2) / (2g) = 12 +( 60-1) / 20 = 14,95~ 15 m. QCM n°9, 10 : tube au néon. Un tube luminescent utilisé pour l'éclairage contient des atomes de néon. Le volume interne du tube est un cylindre de longueur L = 1,20 m et de diamètre d = 42 mm. A la température de fonctionnement du tube, la vitesse des atomes est 0,62 km /s. Masse molaire du néon : M =20,18 g/mol ; 1 eV = 1,6 10-19 J ; NA = 6,022 1023 mol-1. Calculer en eV l'énergie cinétique d'un atome de néon. masse d'un atome de néon : m = M / NA =20,18 / 6,022 1023  =3,35 10-23 g = 3,35 10-26 kg ; v = 620 m/s Ec = ½mv2 = 0,5 *3,35 10-26 *6202 =6,44 10-21 J 6,44 10-21 /1,6 10-19 =0,0402 eV. La densité particulaire dans le tube est D= 1,5 1023 atomes par m3. Calculer l'énergie cinétique totale ( en J)  des atomes contenus dans le gaz. Volume du tube : pr2L = 3,14 *(42 10-3)2 * 1,20 =6,65 10-3 m3. Nombre d'atomes de néon dans le tube : 6,65 10-3 *1,5 1023 =9,975 1020 atomes Energie cinétique totale : 9,975 1020 *6,44 10-21 =6,4 J. QCM n°11,12, 13 : solénoïde. Champ magnétique terrestre  à Paris : composante horizontale : 2,0 10-5 T ; inclinaison magnétique 64,5 ° ( angle que fait le champ par rapport à sa composante horizontale) Calculer la valeur du champ magnétique terrestre à Paris. 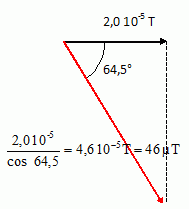Solénoïde : L = 50 cm ; N = 200 spires ; l'axe fait un angle de 50 ° par rapport au méridien magnétique. Une aiguille aimantée mobile est placée au centre du solénoïde. Si l'intensité du courant  est I, l'aiguille tourne de 90°. Quelle est la valeur du champ créé par le solénoïde ? 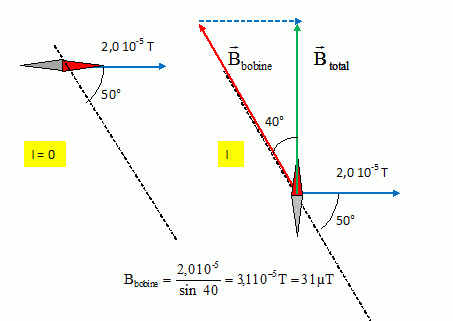Quelle est l'intensité du courant I ? (µ0 = 4 p 10-7) B = µ0 n I avec n = 200 / 0,5 = 400 spires par mètre. B =3,1 10-5 = 4 p 10-7 *400 * I ; I = 0,062 A = 62 mA. QCM n°14 : frottement fluide. F = k v2. Quelle est l'unité de k ? force = masse  * accélération  =masse * longueur / temps2 ; [F] = M L T-2. [v2]= L2 T-2 ;  [k] = M L T-2 L-2 T2 = ML-1. ( kg m-1) QCM n°15 : chute libre. Deux pierres A et B ponctuelles sont distantes de 0,4 m ; A est au dessus de B. A t = 0, on lâche A ; quand A a parcouru d = 0,2 m, on lâche B. Calculer la date de la rencontre. g = 9,8 S.I. Axe vertical orienté vers le bas, origine A. zA = ½gt2 = 4,9 t2 ; zB = ½g(t-t0)2 +0,4. 0,2 = 4,9t02 ; t0 =(0,2 /4,9)½ =0,202 s. Rencontre : zA =zB ; 4,9 t2 =4,9(t-0,202)2 +0,4. 0 = -1,9796 t + 0,2 + 0,4 ; t = 0,3 s. QCM n°16 à 20 : champ magnétique terrestre. Ce champ est assimilable à celui d'un aimant droit orienté suivant l'axe des pôles. 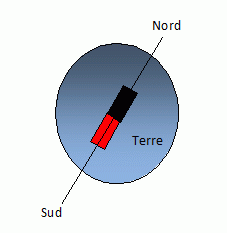Parmi les propositions suivantes, lesquelles sont vraies ? A. au pôle nord une boussole ne prend aucune orientation. Vrai. B. Dans l'hémisphère sud, le pôle nord de la boussole est orienté vers le pôle sud. faux. C. le champ magnétique terrestre est nul à l'équateur. faux. La boussole des tangentes est un dispositif constitué d'une bobine plate verticale, comportant N spires de rayon R, au centre de laquelle est placée une aiguille aimantée mobile dans un plan horizontal. 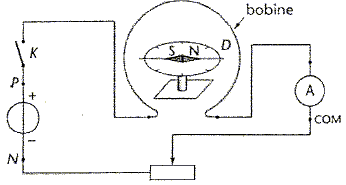On réalise le montage ci-dessous : Lorsque le circuit est ouvert, l'aiguille de la boussole est orientée selon la composante horizontale Bh du champ magnétique terrestre ( on appelle D cette direction ). On oriente la bobine de telle sorte que son plan contienne D. Lorsque le circuit est fermé, la bobine parcourue par un courant crée en son centre O un champ magnétique B0 tel que représenté sur le schéma suivant : 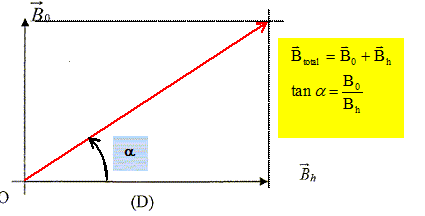L'aiguille tourne alors d'un angle a par rapport à la direction D. R = 12,5 cm ; N = 6 spires jointives ; I = 1,2 A ; Bh = 2,3 10-5 T ; B0 = µ0 NI / (2R). Calculer a. B0 = 4 p 10-7 * 6*1,2 / (2*0,125) =3,62 10-5 T tan a = 3,62 / 2,3 = 1,572 ; a = 57,6 °. On remplace la bobine plate par un solénoïde : N = 100 spires ; I = 100 mA. Le champ magnétique créé au centre du solénoïde est égal à B0. Calculer la longueur L du solénoïde. B0 =3,62 10-5 = µ0 n I avec n = N / L  spires par mètre. n = 3,62 10-5 /( 4 *3,14 10-7*0,1) =288,2 ; L = N /n = 100/288,2 = 0,347 m ~ 35 cm. On place un fil conducteur rectiligne vertical à la distance R du centre de la boussole. Quelle est l'intensité du courant créant au centre de la boussole un champ magnétique de valeur B0 ? Champ magnétique créé  à la distance R du fil : B0 = µ0 I / (2p R) I = B02p R /µ0 =3,62 10-5 *0,125 / (2 10-7) = .

retour -menu