La
présence de nombreux cours d'eau a fort débit permet à certains pays,
comme le canada, d'assurer une importante proportion d'énergie
électrique à base d'hydroélectricité. Les questions qui suivent visent
à examiner comment, par une relation simple, il est possible de donner
une estimation de la puissance maximale disponible à partir de quelques
grandeurs physiques comme le débit volumique Dv ( m3
s-1) et la hauteur de chute H.
On donne Dv = 1,2 m3 s-1;
H = 237 m.
Etude de la
chute d'eau.
En considérant une masse m d'eau qui coule le long d'un plan incliné
comme le ferait un mobile soumis à son poids et à une force de réaction
du plan perpendiculaire à celui-ci,
exprimer
l'accélération a = d2x/dt2 en fonction de g et
a.
Ecrire
la seconde loi de Newton suivant l'axe des x :
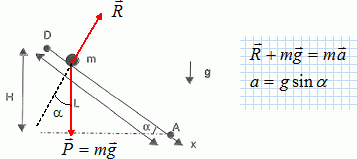
A quelle hypothèse
correspond le fait de considérer la réaction du plan perpendiculaire à
celui-ci ?
On néglige les frottements.
Pour une vitesse initiale nulle,déterminer, à partir
du résultat précédent ou d'un théorème à énoncer, la vitesse vA atteinte par la
masse d'eau lorsqu'elle a parcouru une longueur L sur le plan.
La vitesse est une primitive de l'accélération ( la constante
d'intégration est nulle, car la vitesse initiale est nulle )
v = g sin a t soit t =
v / (g
sin a)
La distance parcourue est une primitive de la vitesse ( la constante
d'intégration est nulle si on choisi l'origine de l'axe en D )
x= ½gsin
a t2.
Remplacer t par son expression : x =½v2 / (g sin a) ; soit en A : vA = (2gL sina)½ = (2gH)½.
Ou bien écrire le théorème de l'énergie cinétique : R, perpendiculaire
au plan ne travaille pas ; le travail du poids est moteur en descente
et vaut mg L sin a.
En
déduire l'expression de l'énergie cinétique correspondante en fonction
de m, g et H.
Ec = ½mvA2
= ½m *2g H = mgH.
Retrouver
ce résultat en invoquant la conservation d'une grandeur énergétique.
On choisit l'origine de l'énergie potentielle en A.
En D, l'énergie mécanique est sous forme d'énergie potentielle de
pesanteur : mgH.
En A, l'énergie mécanique est sous forme cinétique : ½mvA2.
En absence de frottement, l'énergie mécanique se conserve : ½mvA2= mgH.
|
En quoi ce résultat
donne-t-il la valeur maximale de la vitesse VA obtenue ?
Dans la réalité, il faut tenir
compte des frottements. L'énergie mécanique ne se conserve pas.
On
peut s'interroger sur l'intervention des autres éléments du fluide en
écoulement. Pour ce faire, on propose d'utiliser, sans la justifier,
l'équation de Bernoulli qui stipule que dans un écoulement, sous
certaines hypothèses que l'on supposera remplies ici, la grandeur P +½rv2 +rgz a une valeur constante en tous
les poits de l'écoulement.
P désigne la pression, r la
masse volumique de l'eau ( constante), v la vitesse de l'écoulement et
z l'altitude du point.
Sur
la figure ci-dessus, choisir deux points et montrer que l'on peut
retrouver la vitesse VA exprimée ci-dessus.
On choisit les points A et D à la surface de l'eau : les
pressions sont alors égales en A et D à la pression atmosphérique. Le
point D appartenant à une vaste étendue d'eau ( lac ), la vitesse
d'écoulement en D est pratiquement nulle.
PD +½rvD2 +rgzD = PA +½rvA2 +rgzA ;
rgzD =+½rvA2 +rgzA ; gzD =+½vA2 +gzA ; vA2 = 2g(zD-zA)
= 2gH.
|
Puissance
récupérable par la turbine.
Lorsque l'eau arrive avec la vitesse vA sur la turbine, les
pâles de celle-ci exercent une force qui ralentit la vitesse
d'écoulement. On se place ici dans le cas idéal où la vitesse finale
est nulle.
En raisonnant sur
une masse m d'eau qui passe de la vitesse vA à 0, donner le
travail de la force exercée par la turbine ( on
précisera la loi physique employée et la signification des termes ).
Théorème
de l'énergie cinétique, seule la force F travaille
: W =½mvA2 = mgH.
Deduire
de ce résultat la relation qui existe entre la puissance maximale que
l'on peut convertir en électricité dans la centrale hydroélectrique, le
débit volumique Dv et la hauteur de chute H. ( d'autres grandeurs de valeurs constantes sont
nécessaires).
Dv=
volume d'eau qui s'écoule en 1 seconde dans la conduite Dv = m / ( r Dt) d'où m = Dv r Dt.
W
= Dv
r Dt g H ; Pmaxi = W / Dt = Dv
r g H.
A.N : Pmaxi =1,2
*1000*9,8*237 = 2,8 106 W.
En pratique, la puissance P réellement disponible est plus faible.
Comment
peut-on définir un coefficient sans dimension, compris entre 0 et 1,
rendant compte de la part de la puissance disponible récupérée ?
Le coefficient peut être défini par : P / Pmax.
Citer
quelques phénomènes qui expliquent l'écart entre ce qui est disponible
et ce qui est réellement obtenu.
La vitesse de l'eau à la sortie de la turbine n'est pas nulle ; tenir
compte des frottements et des pertes de charge dans la conduite.
Il faut également prendre en compte le rendement du groupe
turbine-alternateur.
Géothermie.
Lorsqu'il est possible d'accéder dans le sous-sol à des nappes
d'eau chaude, on peut envisager de récupérer de l'énergie par un
ensemble de procédés qui fondent la géothermie. Il est ainsi possible
d'utiliser directement, sous forme thermique, une partie de l'énergie
récupérée, pour chauffer des habitations, mais il est également
possible d'envisager une production d'énergie électrique.
Etude d'une centrale géothermique.
Un forage fournit un débit D =250 kg s-1 d'eau chaude à la température q1 = 165°C sous la pression P1 = 7,0 105
Pa. Dans ce état, noté (1), le fluide extrait est composé d'un mélange
d'eau liquide et de vapeur d'eau, dont la composition en masse est
définie par le taux de vapeur x1 = 0,25, correspondant à 25%
de vapeur et à 75 % de liquide. Le concepteur de l'installation doit
alors imaginer un système permettant de tirer parti de cette source
d'énergie, en vue d'optimiser la puissance électrique récupérée.
Une première contrainte découle de ce qu'il n'est pas équivalent de
transformer de l'énergie électrique en énergie thermique et de faire
l'inverse. Ainsi, il est possible de chauffer de l'eau dans une
bouilloire en consommant de l'électricité, il ne suffit pas de verser
de l'eau chaude dans la bouilloire pour espérer récupérer de l'énergie
électrique en attendant que l'eau refroidisse. On dit que la
transformation n'est pas réversible.
Par quel procédé simple peut-on transformer de l'énergie électrique en énergie thermique ( chaleur ) ?
Le passage du courant électrique dans un conducteur s'accompagne d'un dégagement de chaleur ( effet Joule ).
Propriété du mélange eau liquide- vapeur d'eau.
Si on utilise une quantité d'énergie égale à E =104 J, quelle masse d'eau liquide initialement à 10°C peut-on porter à 100°C ? ( l'eau restant liquide ).
E = m c Dq avec c = 4180 J kg-1 °C-1.
m = E / (c Dq) = 104 / (4180*90)=0,02658 ~0,027 kg.
Quelle quantité d'énergie supplémentaire E' faut-il fournir pour vaporiser cette masse d'eau ( la vapeur étant obtenue à 100 °C et la pression étant 105 Pa).
Energie thermique ( chaleur latente ) de changement d'état H2O(l) --> H2O (g) : 44 kJ mol-1.
0,02658 kg = 26,58 g soit 26,58/18 =1,477 mol d'eau ; E' = 44*1,477 ~ 65 kJ = 6,5 104 J.
En comparant E et E' justifier pourquoi la plupart des machines thermiques mettent en jeu des changements d'état ?
E'
est bien supérieure à E ; lors d'un changement d'état physique,
l'énergie mise en jeu est bien supérieure à celle correspondant à la
variation de température de la même masse d'un fluide ( sans changement
d'état).
Une formule approchée donne la pression du changement d'état liquide-vapeur ( L=V) de l'eau à la température q ( °C) :
PL=V = [q/100]4 avec PL=V en atmosphère, que l'on assimilera au bar, c'est à dire à 105 Pa.
Pour quelle température cette expression a-t-elle manifestement été ajustée ?
PL=V = 1 bar si la température est égale à 100 °C.
Justifier l'intérêt de fermer un auto-cuiseur ( cocotte-minute ) avec un couvercle étanche muni d'une soupape.
La pression étant supérieure à 1 bar, la température d'ébullition de
l'eau est supérieure à 100°C : les aliments cuisent plus rapidement.
Justifier pourquoi en haute montagne il est difficile de faire cuire des pâtes.
La pression étant inférieure à 1 bar, la
température d'ébullition de l'eau est infpérieure à 100°C : les aliments
cuisent plus lentement.
Quelle valeur de pression de changement d'état aurait donnée la formule approchée pour la température q1 ?
PL=V = [165/100]4 =7,4 bar.
Récupération de puissance par détente.
Pour amener 1 kg d'eau liquide initialement à q0 = 45,8°C vers l'état (1) défini ci-dessus, il faut fournir une énergie égale à Q = 1,02 106 J kg-1. Si la transformation inverse était possible dans une turbine, c'est à dire s'il ne se posait pas le problème de éversibilité, quelle serait la puissance P récupérée pour le débit D donné ci-dessus ?
D =250 kg s-1 ; P = Q D = 1,02 106 * 250 =2,55 108 W.
En pratique, il faut renoncer à cette solution. On extrait alors la
vapeur du mélange issu du forage. L'organe appelé séparateur (
séparateur 1 ) effectue cette séparation sans nécessiter d'énergie et à
pression constante. On détend la vapeur obtenue dans une turbine (
turbine 1) où l'énergie récupérée par kg de vapeur détendue est w1 = 639 kJ kg-1.
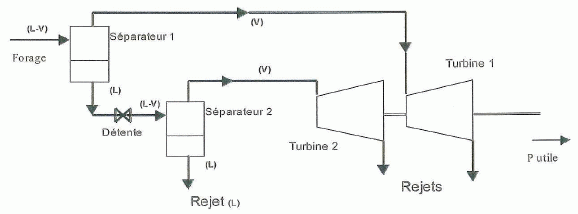
A partir de la composition de (1), calculer le débit massique de vapeur détendue.
25% en masse de vapeur soit D1 =0,25 D = 0,25*250 = 62,5 kg s-1.
En déduire la puissance utile P1 récupérée dans la turbine 1. Commenter.
P1 = D1 w1 =62,5 *639 ~4,0 104 kW.
Cette valeur est très inférieure à la puissance récupérée dans l'hypothèse de la réversibilité.
La solution précédente est perfectible, car il est intéressant de tirer
également profit de la fraction d'eau liquide chaude qui reste après la
première séparation de la vapeur. Une détente de ce fluide permet
d'obtenir, avec un même débit massique, un mélange liquide vapeur dans
l'état (2) : P2 = 1,0 105 bar, q2 = 100 °C et taux de vapeur x2
= 0,12. On peut alors séparer la vapeur ( séparateur 2 ) et la détendre
dans une seconde turbine, où chaque kg de vapeur détendue fournit w2 = 341 kJ kg-1.
Quel supplément de puissance P2 obtient-on ?
250*0,75 = 187,5 kg s-1 de liquide soit 187,5*0,12 = 22,5 kg s-1 de vapeur.
P2 = 22,5 w2 =22,5*341 =7,67 103 kW ~7,7 103 kW.
Puissance totale : 4,0 104 + 7,7 103 = 4,7 104 kW.
|
Notion de cogénération.
Une
telle installation fournit de la puissance électrique, mais rejette
également de l'eau chaude, qui apparaît comme un ressource à valoriser.
On ne peut souvent pas utiliser cette eau de forage pour un usage
domestique, mais récupérer à partir d'elle de l'énergie thermique. On
met alors en jeu un échangeur thermique, dispositif dans lequel l'eau
rejetée et l'eau domestique échangent de l'énergie thermique sans se
mélanger. On négligera dans l'étude qui suit toutes les pertes
thermiques vers l'extérieur.
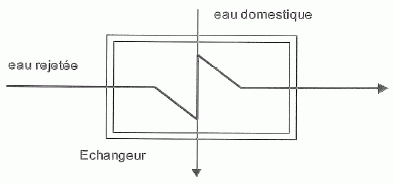
On suppose qu'un débit D d'eau rejetée, initialement à q2 = 100°C, échange avec un même débit D'=D d'eau à usage domestique initialement à q3 = 5°C. Si la température de sortie de l'eau domestique est égale à q4 =60°C, quelle sera la température q5 de sortie de l'eau rejetée ?
Puissance thermique gagnée par l'eau domestique : P1 = D' c (q4-q3)
Puissance thermique cédée par l'eau issue du forage : P2 = D c (q5-q2)
Pas d'échange avec l'extérieur : P1 + P2 = 0 ; q4-q3 + q5-q2 = 0
q5=q3 +q2 -q4 = 5+100-60= 45°C.
On détermine les caractéristiques de l'échangeur thermique de telle manière que l'eau rejetée entre à q2 = 100°C et sorte à q'5 = 10°C. Si les températures d'entrée et de sortie de l'eau domestique restent q3 et q4 précédentes, calculer le rapport D'/D des débits des deux circuits.
D' c (q4-q3) + D c (q'5-q2)=0 ; D' (60-5) +D (10-100)=0 ; 55D' =90 D ; D'/D = 1,6.
|
|


