On considère
ici la conversion d'énergie mise en oeuvre dans un aérogénérateur,
également appelé éolienne. Les hypothèses d'étude sont les suivantes :
le vent est assimilé à un écoulement d'air à vitesse constante v, en
amont de l'éolienne. l'air est assimilé à un gaz parfait de masse
molaire M, de composition molaire approximative : 80 % N2 et 20 % O2.
La température est supposée constante, égale à T ( exprimée en kelvins
). On souhaite estimer la puissance maximale que l'on peut espérer
convertir en puissance électrique avec un aérogénérateur dont la
longueur des pales est L.
Propriétés de l'air.
Rappeler la loi des gaz parfaits.
PV = nRT
|
P: pression du gaz en Pa
V: volume du gaz en m3
n: quantité de matière de gaz en
mol
T: température absolue du gaz en K
R: constante des gaz parfaits. R=8,32 SI
|
déterminer la masse d'une mole d'air.
M= 0,8 M(N2) + 0,2 M(O2) = 0,8*28+0,2*32 =28,8~29 g/mol.
En déduire une valeur de la masse volumique r d'un gaz pafait en fonction de P, T, M et R.
PV = nRT avec n = m / M d'où PV = mRT/M
r = m/V = PM / (RT).
A.N: cas de l'air P= 1,00 105 Pa et T = 300 K.
r =1,00 105*29 10-3 / (8,32*300) = 1,16 kg m-3.
|
Puissance disponible.
On
cherche à exprimer l'énergie cinétique associée au vent, considéré
comme un écoulement d'air. Dans toute la suite on considérera la masse
volumique de l'air comme constante, égale à r = 1,2 kg m-3,
ce qui revient à négliger la compressibilité de ce fluide. Cette
hypothèse est valable tant que la vitesse de l'écoulement est
très inférieure à la vitesse du son dans ce fluide au repos. dans
l'air, cette célérité est donnée par c = [7RT / (5 M]½.
Calculer sa valeur numérique, ainsi que celle du nombre de Mach, défini comme Mn = v/c, pour un vent de vitesse v= 10 m/s à T=300 K. Conclure.
c = [7*8,32*300 / (5 *0,029]½=347 ~3,5 102 m/s.
Mn = 10 / 347 = 0,029.
v est très inférieure à c : l'hypothèse énoncée ci-dessus s'applique.
|
Considérone le disque de rayon L, balayé par les pales sur un tour.
Exprimer son aire S ?
S = p L2.
Si
l'on fait abstraction de la modification de l'écoulement due à
l'éolienne, exprimer la masse m d'air qui traverse S pendant une durée
t en fonction de t, S, v et r. En déduire l'expression du débit massique Dm = m/t.
Volume d'air : S vt ; masse d'air : m = S v t r.
Dm= m / t = S v r.
Donner l'expression de l'énergie cinétique Ec de la masse m s'écoulant à la vitesse v. En déduire l'expression de la puissance P0 = Ec/t.
Ec = ½m v2 = ½m v2 =½S v t r v2 =½ S t r v3 ; P0 = ½ S r v3.
A.N : L= 39 m ; v = 10 m/s ; P0 =0,5 *3,14*392*1,2*103 =2,86 106 ~2,9 106 W.
En
pratique, cette puissance n'est pas récupérable intégralement,
puisqu'il y a nécessairement interaction de l'aérogénérateur et du
vent. On examine un modèle simple illustrant ce fait et prenant en
compte la déviation des lignes de courant par l'hélice. Si on note v'
la vitesse du vent en aval de l'éolienne, on peur considérer que toute
l'énergie cinétique Ec, calculée ci-dessus, n'est pas convertie :
l'écoulement d'air conserve une certaine énergie cinétique E'c en aval.
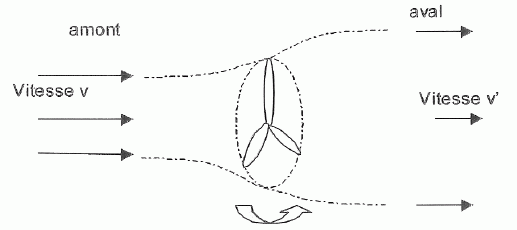
Pour une durée t, la masse d'air m mise en jeu se conserve entre l'amont et l'aval.
Exprimer la différence d'énergie cinétique E'c-Ec en fonction de m, v et v'.
½mv'2-½mv2 = ½m( v'2-v2 ).
Le
débit d'air est également affecté par la présence de l'éolienne. La
relation déterminée ci-dessus, entre t, m, S et v, doit également être
modifiée. On considèrera qu'il suffit de remplacer v par ½(v+v').
Etablir
l'expression de la puissance disponible pour la conversion par
l'éolienne, en fonction du rapport des vitesse r = v' / v sous la forme
: P =½P0 (1-r2) (1+r).
P =(Ec-E'c) / t =½m( v2-v'2 ) t avec m = ½ S (v+v') t r.
P = 0,25 (v+v') r ( v2-v'2 )= 0,25 S r v3 (1+r) (1-r2) =½P0 (1-r2) (1+r).
On se propose d'examiner les conséquences de cette loi.
Interpréter les limites r=0 et r=1. Vous paraissent-elles plausibles ?
r=0
: la vitesse du vent en aval de l'éolienne est nulle ; r = 1 : la
vitesse du vent en aval est identique à la vitesse en amont : ce n'est
guère plausible car il y a interaction entre l'éolienne et l'air.
Tracer le graphe de P / P0 en fonction de r pour r variant de 0 à 1.
r
|
0
|
0,1
|
0,2
| 0,3
|
0,4
|
0,50
|
0,6
|
0,7
|
0,8
|
0,9
|
1
|
| P / P0=0,5(1-r2)(1+r) |
0,5
|
0,54
|
0,58
| 0,59
|
0,59
|
0,56
|
0,51
|
0,43
|
0,32
|
0,18
|
0
|
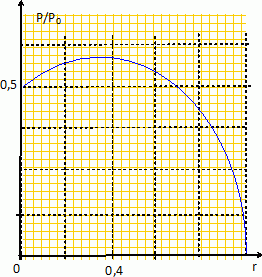
Déterminer la (les) valeur(s) de r donnant P/P0 maximal et la (les) valeur(s) correspondante(s) de P/P0.
Dériver P/P0 par rapport à r et chercher la valeur de r qui annule cette dérivée :
-2r(1+r) +(1-r2) =0 ; 3r2+2r-1 = 0 ; D =16 ; r1 =(-2+4) / 6 ~ 0,33 et r2 = (-2-4) / 6 ( valeur négative, à ne pas retenir ).
P/P0 = 0,5(1-0,332)*1,33 =0,59.
Pour
les conditions de vent et les paramètres caractéristiques de
l'aérogénérateur donnés ci-dessu, déterminer la puissance maximale que
l'on peut espérer convertir en électricité.
P = 0,59 P0 = 0,59 *2,9 106 =1,72 106 ~1,7 106 W= 1,7 103 kW.
Les articles et études sur le sujet de la production d'énergie éolienne reprennnent parfois la formule suivante : P =L2[v1/10]3 où v1 est la vitesse du vent ( m/s) , L longueur en mètre et P puissance en kW.
L'étude précédente permet-elle de rendre compte de ce résultat ?
P =392[10/10]3 = 392 =1,5 103 kW.
Cette valeur est comparable à celle calculée ci-dessus. l'étude rend compte de ce résultat.
Un ordre de grandeur de durée annuelle d'utilisation est 2300 heures par an.
Que devient la puissance moyenne annuelle ?
Energie produite : 1,7 103 *2300 =3,9 106 kWh
1 an = 365*24 =8760 heures.
3,9 106 / 8760 = 4,5 102 kW.
|
Recherche de sites propices.
Une
étude lancée sur le territoire français pour identifier les sites
propices à une installation de fermes de vent a mis en évidence une
nette prédominance des zones côtières et de la vallée du Rhône.
Justifier brièvement.
Les vents dominants soufflent de l'ouest : ils sont plus forts et plus fréquents sur les côtes qu'à l'intérieur du pays.
Le couloir rhodanien est fréquemment parcouru par un vent du nord, le mistral.
Quelles raisons peuvent expliquer, sur la plupart des sites, la différence de vitesse de vent entre jour et nuit ?
Le sol chauffe le jour, notamment en été, ce qui créé des turbulences
dans l'air et augmente le vent. La nuit le refroidissement de l'air par
le sol, stabilise l'air.
De nombreuses associations s'opposent à l'installation de parcs éoliens
en invoquant des nuissances visibles et sonores. Les hélices des
éoliennes sont en effet placées sur des mats de grande hauteur,
couramment de plusieurs dizaines de mètres.
Justifier ce choix alors qu'il ne fait qu'accentuer la visibilité des éoliennes à grande distance.
A quelques dizaines de mêtres de hauteur, les vents sont plus forts et
plus réguliers qu'au niveau du sol. Au sol il y a de nombreux obstacles
( arbres, bâtiments) qui perturbent le vent.
Expliquer brièvement qu'un éolienne puissent être à l'origine d'un son perçu par l'oreille humaine.
Par rapport au vent, quelle zone est à priori la plus concernée ( amont, en aval , latéral ) ?
Le bruit est lié aux pâles qui fendent l'air.
Les engrenages de précision sont assez silencieux ; les nacelles sont capitonnées.
Les pâles tournent assez lentement et les bruits émis sont perçus par l'oreille hgumaine.
La source de bruit est l'éolienne ; le bruit se propage dans toutes les directions à partir de la source.
Les ondes sonores se propagent plus vite dans la direction du vent : la zone en aval sera donc plus bruyante.
|
|


