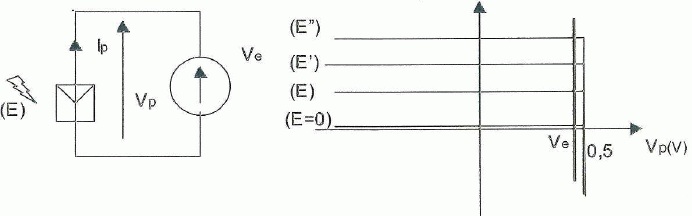Une
part importante de l'énergie disponible sur Terre provient du
rayonnement du Soleil. Celui-ci émet en effet des ondes
électromagnétiques, dont de la lumière visible, de manière isotrope,
c'est à dire identique dans toutes les directions. Dans cette partie,
la température est exprimée en kelvins.
Puissance
surfacique de rayonnement solaire.
Le Soleil suit de manière satisfaisante un modèle très simple, qui
suppose que chaque élément de sa surface émette une puissance
surfacique f = s TS4, où s = 5,67 10-8 W m-2
K-4 est appelée constante de Stefan. TS est la
température de la surface du Soleil.
Calculer
la puissance émise par le Soleil.
On donne TS = 5800 K ; rayon du Soleil : RS = 7,0
108 m.
f = s TS4 = 5,67 10-8
*58004=6,416 107 W m-2.
Surface du Soleil : 4 p R2S = 4*3,14 *(7,0 108 )2=6,16
1018 m2.
P =6,416
107 *6,16 1018
= 3,95 1026 ~ 4,0 1026 W.
Le
modèle évoqué ici implique une autre loi, qui veut que le domaine
spectrale du rayonnement émis soit lié à la température de surface. le
spectre continu d'émission présente en effet un maximum à une longueur
d'onde lm, qui
est liée à la température T du corps par la loi de Wien. Celle-ci
stipule que lmT
est une constante universelle de valeur numérique 3 10-3 S.I.
Préciser
cette unité.
Longueur d'onde en mètre et température en kelvin : [lmT] = L K-1.
( m K-1)
Calculer lm pour le Soleil.
lm = 3 10-3
/5800 =5,17 10-7 ~5,2 10-7 m = 0,57 µm.
Dans quel
domaine spectral se situe le rayonnement émis par le Soleil ? Commenter.
40 % de l'énergie est émise dans
le domaine visible ; 50 % dans l'infrarouge et 10 % dans l'ultraviolet.
|
Justifier
que, bien que l'on néglige toute absorption de l'onde à
l'extérieur du Soleil,
la
puissance surfacique f reçue
à une distance d du centre du soleil dépende de d.
Puissance surfacique rayonnée par le
Soleil ( loi de Stefan : s TS4 ;
Surface du Soleil :
4 p R2S ;
Puissance totale rayonnée par le Soleil : s TS4 4 p R2S ;
On considère qu'il n'y a pas de pertes : cette puissance se conserve.
A la distance d du soleil, le flux surfacique f reçu orthogonalement est :
f 4 p d2 = s TS4 4 p R2S ;
f = s TS4 (RS / d)2.
A.N : flux surfacique reçu
à la surface de la Terre, d =D = 1,5 1011 m.
f = 5,67 10-8
*58004 (7 108 / 1,5 1011)2=
1,4 103 W m-2.
|
Rôle de
l'atmosphère.
Si l'on considère D très supérieure au rayon terrestre RT,
on peut considérer que la terre intercepte le rayonnement solaire par
un disque de rayon RT. Sachant que 34 %
du rayonnement ainsi reçu est réfléchi par l'atmosphère, quelle est la
puissance totale reçue du Soleil sous forme de rayonnement ?
Surface
du disque de rayon RT : S = p RT2 ;
Puissance reçue : f S = 1,4 103
*3,14*(6,4 106)2 =1,8 1017 W.
En tenant compte de la réflexion par l'atmosphère : (1-0,34) 1,8 1017 = 1,2 1017 W.
L'énergie
mise en jeu par les activités humaines est estimée à 1,4 1014
kWh pour une année.
Quel
est l'ordre de grandeur du rapport entre l'énergie annuelle reçue du
Soleil et cette énerie associée aux activités humaines ?
Energie annuelle reçue du Soleil : 1 an = 365*24 = 8,76 103
heures.
1,2 1017 W = 1,2 1014 kW ; d'où l'énergie reçue
annuellement du Soleil : 1,2 1014 *8,76 103 ~1,1
1018 kWh.
Puis : 1,1 1018 / 1,4 1014 ~7,5 103.
La majeure partie du rayonnement visible provenant du soleil et non
réfléchi par l'atmosphère traverse celle-ci et parvient à la surface de
la Terre. Par ailleurs la surface terrestre émet elle aussi un
rayonnement thermique qui suit la loi de Wien énoncée ci-dessus. En
prenant une température raisonnable pour la température moyenne de la
surface de la Terre, estimer dans quel
domaine spectral se situe la longueur d'onde du maximum d'émission du
rayonnement terrestre.
Température
moyenne : 15 °C soit 273 +15 = 288 K.
Loi de Wien : lmT = 3 10-3
; lmT= 3 10-3
/ 288 = 1,0 10-5
m = 10 µm ( domaine infrarouge).
L'atmosphère n'est pas transparente dans ce domaine, elle réalise ainsi
une sorte de piège à rayonnement en laissant entrer le rayonnement
solaire et en piègeant le rayonnement terrestre.
Comment
appelle t-on cet effet ?
Ce
rayonnement va traverser l'atmosphère qui en absorbe 90 %, ce qui
réchauffe l'atmosphère, qui elle même réchauffe le sol. C'est l'effet de serre.
Cet
effet e-t-il pour conséquence une augmentation ou une diminution de la
température terrestre ?
L'efet de serre augmente la température terrestre.
Certaines activités humaines utilisent le même effet, en exploitant la
propriété du verre d'être transparent dans le visible et absorbant dans
le domaine de rayonnement des corps à tempréture ambiante.
Citer un
exemple.
Les cultures sous serre, la production d'eau chaude dans un capteur
thermique solaire.
Les cellules
photovoltaïques :
L'énergie solaire peut
être
utilisée directement sous forme d'énergie thermique pour chauffer de
l'eau ou des locaux ; mais il peut être souhaitable de convertir cette
puissance reçue par rayonnement en puissance électrique. Alimenter un
moteur électrique, un ordinateur ou un dispositif d'éclairage,
recharger un accumulateur, constituent des exemples d'applications
nécessitant une conversion en un signal électrique. On étudie ici les
aspects électriques caractéristiques d'une cellule photovoltaïque.
Caractéristique
d'une cellule unique.
La figure ci-dessous représente une caractéristique tension-intensité
pour une cellule photovoltaïque élémentaire, éclairée par un
rayonnement d'éclairement ( puissance par unité de surface) E fixé. Les
conventions d'orientation des tension et intensité sont indiqués. On
branche un voltmètre continu aux bornes de la cellule considérée,
recevant un éclairement E. On appelle tension à vide ou tension de
circuit ouvert, la valeur Voo mesurée. Faire figurer cette
valeur sur le schéma.
On branche le voltmètre de telle manière que la valeur mesurée soit
positive.
Ayant débranché le voltmètre, on mesure l'intensité de court-circuit ICC
à l'aide d'un ampèremètre continu branché aux bornes de la cellule,
celle-ci recevant toujours l'éclairement E. Faire figurer ICC sur le schéma.
La tension est nulle aux bornes de la cellule en court-circuit.
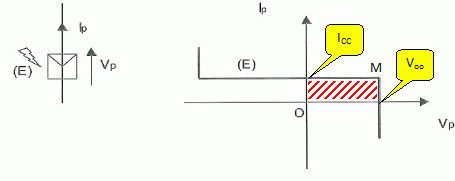
Mettre en
évidence la portion de la caractéristique correspondant à un
fonctionnement en générateur électrique, c'est à dire où la puissance
électrique est positive.
Quel est
le point de la caractéristique où cette puissance est maximale ?
( on l'indiquera par la lettre M ).
Puissance en courant continu = Voo ICC.
Lorsque l'éclairement E varie, la caractéristique évolue et on indique
schématiquement un réseau simplifié de caractéristiques,
paramétré par différentes valeurs de E ( E" > E' >E >0 ).
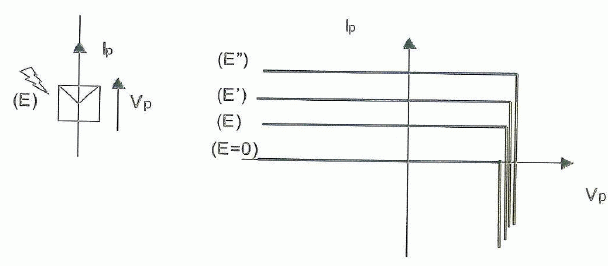
Le comportement d'une cellule photovoltaïque est
bien représenté par la fonction
caractéristique :
i = g E- Is [ exp(VP/VT)-1].
g est un coefficient qui tient compte de l'aire de la cellule et du
matériau, il rend compte de l'effet photovoltaïque, nous le prendrons
ici égal à g = 4,0 10-4 A W-1 m2.
VT est un paramètre homogène à une tension qui ne dépend que de la température, il vaut VT = 0,025 V à 300 K. Nous supposerons cette valeur constante par la suite.
IS est une intensité caractéristique, que nous supposerons constante, égale à IS = 1,0 10-10 A.
Comment s'exprime l'intensité de court-circuit ICC en fonction de l'éclairement E ?
En court-circuit, la tension VP aux bornes de la cellules, est nulle : ICC = gE-IS(exp(0) -1) = gE ; ICC = 4,0 10-4 E.
E(W m-2)
|
100
|
400
|
700
|
| ICC(A)= 4,0 10-4 E. |
4,0 10-2
|
0,16
|
0,28
|
Comment s'exprime la tension de circuit ouvert ( tension à vide ) VCO en fonction de E et des paramètres ?
L'intensité est nulle en circuit ouvert : g E= Is [ exp(VCO/VT)-1].
g E/ Is =exp(VCO/VT)-1 ; g E/ Is +1 = exp(VCO/VT) ; VCO/VT = ln[g E/ Is +1]
VCO= VT ln[g E/ Is +1] = 0,025 ln[4,0 10-4 E /1,0 10-10 +1] ~ 0,025 ln[4 106 E]
| E(W m-2) |
100
|
400
|
700
|
| VCO (V)~ 0,025 ln[4 106 E] |
0,495
|
0,530
|
0,544
|
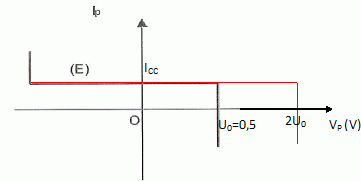
Par la suite, on considèrera la tension en circuit ouvert constante, notée U0 = 0,50 V.
On branche la cellule sur un dipôle extérieur imposant une tension constante Ve = 0,45 V ( caractéristique représentée ci-dessous ).
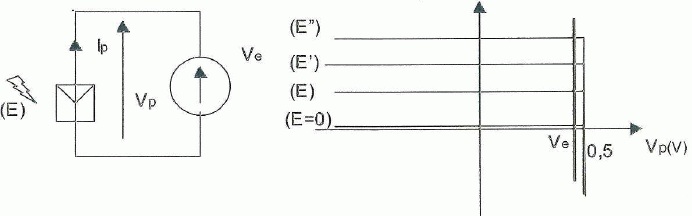
Comment évolue l'intensité qui circule dans le circuit lorsque l'éclairement E varie ? Comment s'appelle une loi de ce type ?
i = g E- Is [ exp(VP/VT)-1] avec VP = 0,45 V.
i = 4,0 10-4 E -1,0 10-10[ exp(0,45 / 0,025)-1] =4,0 10-4 E -6,56 10-3.
L'intensité est une fonction affine de l'éclairement.
| E(W m-2) |
100
|
400
|
700
|
i =4,0 10-4 E -6,56 10-3 (A)
|
3,34 10-2
|
0,153
|
0,273
|
Esquisser le graphe donnant l'intensité en fonction de l'éclairement.
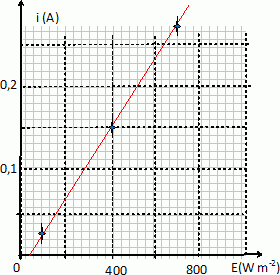
La cellule considérée a une surface S = 10 cm2.
Déterminer pour les 3 éclairements, la puissance électrique Pe donnée par la cellule au circuit extérieur.
| E(W m-2) |
100
|
400
|
700
|
Pe(W) = i Ve
|
3,34 10-2*0,45 =0,015
|
0,153*0,45=0,069
|
0,273*0,45 =0,12
|
Pr( pissance reçue par éclairement) ( W)
|
0,10
|
0,40
|
0,70
|
| rendement : Pe / Pr |
0,15
|
0,17
|
0,17
|
S = 10 10-4 m2 ; Pr = E S = 10-3E.
La puissance qui n'est pas convertie en puissance électrique est convertie en puissance thermique.
|
Association de cellules.
On
souhaite examiner l'intérêt et les propriétés des associations de
cellules photoélectriques identiques en parallèle ou en série. Chacune
a individuellement la caractéristique réprésentée ci-dessus et leur
éclairement est supposé identique.
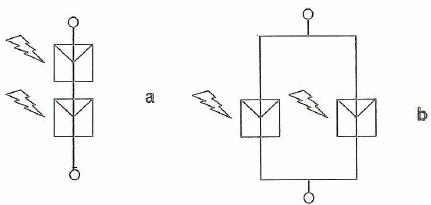
On associe en série deux cellules ; représenter la caractéristique de l'association.
L'intensité est la même en tout point d'un circuit série ; additivité des tensions.
Pour n cellules en série, la tension à vide aux bornes est n U0.
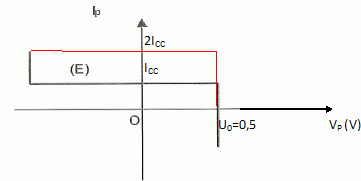
Même question pour une association en parallèle.
La tension est le même aux bornes de cellules en parallèle ; additivité des intensités.
Mêmes questions pour l'association suivante.
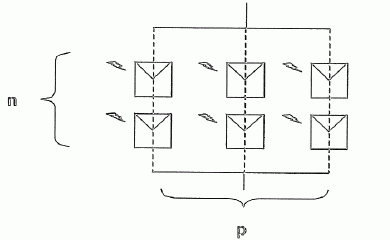
|
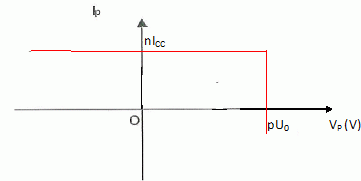
|
Un
panneau totalise 72 cellules. Il est connecté à un dipôle extérieur de
résistance interne négligeable et de tension caractéristique Ve
légèrement inférieure à 18 V.
Proposer des valeurs de p et n pour un bon fonctionnement.
Ve = p U0 = 18 ; p =18/0,5 = 36 ; par suite n =2.
Si chaque cellule de l'association précédente reçoit individuellement Pr= 0,70 W solaire convertis avec un rendement de 17%, quelle est la puissance cédée au dipôle extérieur ?
P = 72*0,70 *0,17 = 8,57 ~8,6 W.
Quelle est l'intensité du courant qui circule entre le panneau et le dipôle ?
I = P/ U = 8,57/ 18 = 0,476 ~0,48 A.
Quelle
est l'allure du graphe donnant la puissance électrique cédée par la
cellule au circuit externe, en fonction de l'éclairement incident ?
L'intensité
est une fonction affine de l'éclairement. A U constante, la puissance
est proportionnelle à l'intensité : la puissance est donc une fonction
affine de l'éclairement.
Si le dipôle extérieur est une batterie d'accumulateurs permettant le
stockage d'énergie convertie, il peut être intéressant de prendre en
compte sa résistance interne, proposer
un schéma faisant apparaître la caractéristique modifiée de ce dipôle
et indiquer comment est affecté le graphe précédent.
La tension U aux bornes de l'accumulateur n'est plus constante ( U=
e-rI acec e : fem et r : résistance interne de la batterie ).
La puissance reçue vaut alors : P = UI = (e-rI)I = eI-rI2.
En
cours d'utilisation de l'association précédente, la surface du panneau
n'est pas uniformément éclairée. Certaines cellules individuelles ne
reçoivent plus l'éclairement E, mais une valeur nettement inférieure
E'. Proposer une description de l'état de fonctionnement des cellules mal éclairées et des phénomènes qui s'en suivent.
La tension aux bornes des cellules mal éclairées ne change pas, par
contre l'intensité du courant délivrée par ces cellules est bien
inférieure à la valeur précédente.
Un article.
Dans un quotidien national, un article présente une des plus grandes
centrales solaires photovoltaïque du monde, qui se trouve au Portugal (
Amareleja ). La puissance affichée est 46 mégawatts, pour 2520 modules
photovoltaïques de 74 m2 qui suivent le soleil dans sa
rotation apparente. Avec 2800 heures de soleil par an, la production de
la centrale doit économiser 86 000 tonnes de gaz à effet de serre.
La puissance de 46 MW est-elle plausible ?
72 cellules de surface totale 720 cm2 fournissent une puissance d'environ 9 W. (soit 125 W m-2).
Surface totale des 2520 modules : S = 2520*74 =1,86 105 m2.
Puissance : 1,86 105 *125 ~2 107 W = 20 MW.
Cette valeur est du même ordre de grandeur que celle indiquée dans le texte.
.
Comment doit-on comprendre l'affirmation concernant léconomie de gaz à effet de serre ?
La
puissance de 46 MW devrait être fournie par une centrale thermique
brûlant un combustible fossile et rejetant du dioxyde de carbone.
|
|