Lumière Laser ; diffraction : concours Eni-Geipi-Polytech 2010.

La lumière d’un LASER est composée d’un mélange de très nombreux “trains d’ondes”, c’est-à-dire de “salves”. Pour réaliser un LASER, on doit réaliser les deux conditions suivantes : - utiliser un matériau capable d’émettre le rayonnement désiré - faire traverser ce matériau de nombreuses fois par la lumière avant qu’elle sorte du LASER pour l’amplifier et la “réguler” Dans la plupart des LASER, on oblige donc la lumière à effectuer de nombreux allers-retours à travers le matériau grâce à un jeu de miroirs (partiellement) réfléchissants : 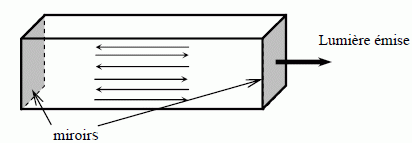On rappelle : la célérité de la lumière dans le vide et dans les milieux gazeux c = 3,00.108m.s-1 la constante de Planck : h = 6,626.10-34J.s Pourquoi faut-il que la distance correspondant à un aller-retour soit un multiple de la longueur d’ondes ? La lumière réfléchie plusieurs fois par les miroirs  interfére avec elle-même. Il faut que les ondes qui se superposent soient en phase   En conséquence, seules quelques ondes  peuvent être présentes dans la cavité. Ces ondes sont appelées les modes de résonance, pour lesquelles la longueur d'onde est un multiple de la distance aller-retour. Dans un LASER hélium-néon, la cavité mesure une longueur L = 23,0 cm. La lumière émise a de plus une longueur d’onde λ = 632,9 nm. Calculer la durée t d’un aller-retour. t = 2L/c = 0,46 / 3,00.108 = 1,53 10-9 ~1,5 10-9 s. On constate qu’un train d’onde émis par ce laser dure en moyenne Δt =0,5 μs. En déduire : le nombre N1 d’allers-retours moyen que fait la lumière dans la cavité pendant cette durée, N1 = Dt / t = 0,5 10-6 / 1,53 10-9 ~326. le nombre N2 de périodes d’oscillations de cette onde. N2 = 2L / l = 0,46 / (632,9 10-9) =7,27 105 ~7,3 105. Quel est le domaine de longueurs d’onde correspondant à la lumière visible ? Les longueurs d'onde de la lumière visible sont comprises entre 400 nm et 800 nm. Quelle énergie transporte un photon de la lumière émise par ce LASER ? E = h c / l = 6,626.10-34*3,00 108 / (632,9 10-9)= 3,14 10-19 J. On place sur le trajet du faisceau émis par le laser une plaque fissurée, et on souhaite mesurer la largeur a de la fissure. On enregistre l’intensité lumineuse reçue le long d’un axe horizontal sur un écran perpendiculaire au faisceau du laser, placé à une distance D = 32 cm après la fissure, et on obtient la courbe présentée ci-dessous. 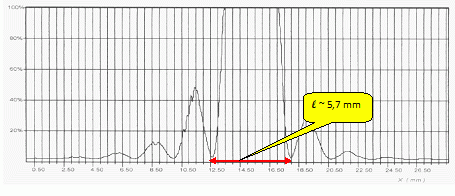Comment appelle-t-on le phénomène observé ? Diffraction par une fente dont la largeur doit être du même ordre de grandeur que la longueur d'onde. On propose plusieurs relations entre la largeur l de la tache centrale, D, λ et la largeur a de le fissure. Choisir la relation exacte. Ecrire l’équation aux dimensions de la solution que vous avez retenue. l =2λD/a ; l =λ/a ; l =2D / (λa );  l =a/2λ ; l =aD/λ. l, l, D, a s'expriment en mètre ; [2λD/a] = L L L-1 = L, l'expression peut convenir. [λ/a] est sans dimension ; ne convient pas. [2D / (λa )] = L-1, ne convient pas. [aD/λ] = L peut convenir, mais la valeur numérique est beaucoup trop grande.  Calculer la largeur de la fissure. a = 2λD / l = 2*632,9 10-9* 0,32 / (5,7 10-3) =7,1 10-5 m. Quelle serait la largeur approximative de la tache centrale si on utilisait un laser émettant de la lumière bleue au lieu de lumière rouge ? ( 12 mm ; 0,5 mm ; 4 mm ; 7 mm ; 80 µm) La longueur d'onde du bleu est de l'ordre de 400 nm. l =2λD/a = 2*400 10-9*0,32 / (7,1 10-5 ) ~3,6 10-3 m. La valeur 4 mm est à retenir. ..

menu