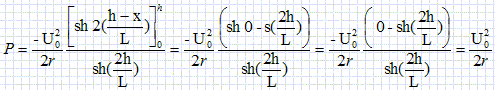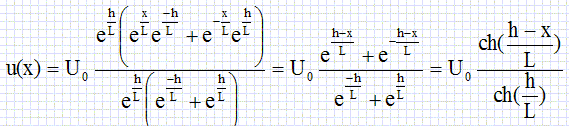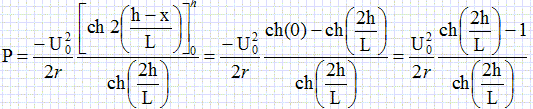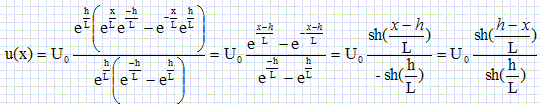Un
câble coaxial rectiligne est constitué par un conducteur
cylindrique homogène plein (appelé l’âme)
parcouru par un courant axial et par un conducteur coaxial
creux,
parcouru par le courant de retour. On note r
la résistance par unité de longueur.
Les
deux conducteurs sont séparés par un
matériau isolant dont la faible conductivité est à l’origine d’un
courant de
fuite qui circule radialement entre les deux conducteurs. On note gf la
conductance de fuite par unité de longueur. Données :
r = 10 mW m-1 ; gf
=1,0 10-10 S m-1.
Soient
u(x) la tension entre les deux conducteurs à l’abscisse x,
et i(x) l’intensité du courant dans l’âme (figure 2b).
Comme l’indique la figure 2b, une
longueur élémentaire dx de câble a
une résistance rdx et une conductance
de fuite gf dx.
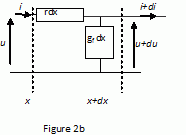
Utiliser
les indications de la figure 2b pour établir la relation entre
l’intensité et
la dérivée première du/dx de la tension.
Additivité des tensions : u = u+du + rdx i ; du +rdx i = 0 ; i = -1/r du/dx (1).
Etablir la relation
entre la
tension et la dérivée première de l’intensité (on négligera le
terme du
deuxième ordre qui apparaît).
u + du = -di / ( gfdx) = -1/gf di/dx ; le terme du est négligeable compte tenu de la longueur du câble.
u ~ -1/gf di/dx (2)
En déduire
l’équation
différentielle suivante : d2u/dx2-u/L2
=0.
Dériver (1) par rapport à x : di/dx = -rd2u/dx2 puis tenir compte de (2) : -1/r d2u/dx2 = -gf u.
d2u/dx2 -rgf u = 0 ; on pose L = 1/(rgf)½.
Exprimer
la constante L, préciser sa
dimension, puis calculer sa valeur.
L = 1/(rgf)½ ; r est en W m-1 ; gf est en S m-1 soit W-1 m-1 ; rgf est en m-2 ; (rgf)½ est en m-1 ; L = 1/(rgf)½ est en mètre.
L = (0,01 * 10-10)-½ =1,0 106 m.
Une
extrémité du câble, qui est de très
grande longueur, est reliée à une source de tension continue U0. On
note u(0)=U0 .
Intégrer l’équation
différentielle et en déduire l’expression de la tension u(x).
Solution générale de l'équation différentielle : u(x) = A exp(x/L) + B exp(-x/L) avec A et B des constantes.
u(0) = U0 = A + B.
i = - 1/r du/dx = -1/r [ A / L exp(x/L)-B / Lexp(-x/L)] ; i(L) = 0 = -1/(rL) [ A exp(1)-B Lexp(-1)]
A exp(1)=B Lexp(-1) ; B = A exp(2)
par suite : A = U0 / ( 1+exp(2)) ; B =U0 exp(2) / ( 1+exp(2)).
Exprimer l’intensité
i(x). Montrer qu’il
apparaît
une résistance caractéristique Rc et calculer sa
valeur.
Rc = u(x) / i(x) ; u(x) =U0 / ( 1+exp(2)) [ exp(x/L) + exp(2)exp(-x/L) ]
i(x) = -U0/(Lr( 1+exp(2))) [ exp(x/L)- exp(2) exp(-x/L)]
Rc = -Lr [ exp(x/L) + exp(2)exp(-x/L) ] / [ exp(x/L)- exp(2) exp(-x/L)]
Rc(0) = Lr[1+exp(2)] / [exp(2)-1] = Lr coth(2)
Rc(0) = 1,0 106 *0,01 = 1,3 104 W.
|
On
considère maintenant un câble de même
nature et de longueur h, qui relie la
source de tension continue U0
(en x=0) à l’entrée verticale d’un oscilloscope d’impédance d’entrée
considérée
comme infinie.
Quelle est la valeur
de
l’intensité i(h) ?
i(h) = 0
|
Montrer que la
tension s’écrit : u(x) = U0
ch((h-x) / L) / ch((h/L) . On rappelle
que : ch(a) = ½(ea+e-a).
i(h) = 0 ; i(h) = -U0/(Lr( 1+exp(2))) [ exp(h/L)- exp(2) exp(-h/L)] = 0.
d'où : exp(h/L)- exp(2) exp(-h/L) =0 soit : exp(2) = exp(2h/L)
Repport dans u(x) :
u(x) =U0 / ( 1+exp(2h/L)) [ exp(x/L) + exp(2h/L)exp(-x/L)].
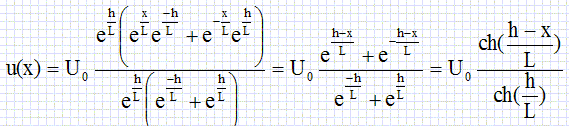
Exprimer l’intensité
i(x).
On rappelle que : d( ch(a) /da = sh(a).
i = - 1/r du/dx =U0 sh((h-x)/L) / (rL ch(h/L) ).
Exprimer
la résistance d’entrée
du câble définie par la relation : R0 = u(0) / i(0).
u(0) = U0 ; i(0) =U0 th (h/L) / (rL) ; R0 =r L / th (h/L).
Que
peut-on dire du rapport h/L
? Simplifier alors l’expression précédente. Calculer R0.
Donnée : h=1,0 m. On rappelle
que sh(a)~ a et que ch(a) ~ 1 quand a <<1.
h/L <<1 ; th (h/L) ~ h/L ; R0 ~r L2 / h =0,01 * 1012 = 1010 W.
Exprimer
puis calculer la
puissance P consommée dans le câble.
Conclure.
dp = u(x) i (x) =-1/ r u(x)du(x) /dx = -1/(2r) d(u2(x)) ;
intégrer entre 0 et h :
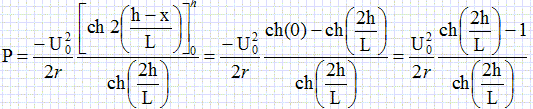
Or h/L <<1 : ch(2h/L) ~1 et P ~ 0 W.
On
suppose maintenant qu’à cause d’un
défaut, l’extrémité du câble reliée à l’entrée verticale de
l’oscilloscope est
en court-circuit.
Quelle
est la valeur de la
tension ucc(h) ?
ucc(h) = 0.
Etablir
les expressions de la
tension ucc(x), de
l’intensité icc(x), de la
résistance d’entrée Rcc0 du
câble.
u(x) =U0 / ( 1+exp(2)) [ exp(x/L) + exp(2)exp(-x/L) ]
u(h) =0 =U0 / ( 1+exp(2)) [ exp(h/L) + exp(2)exp(-h/L) ] ;
exp(h/L) + exp(2)exp(-h/L) = 0 ; exp(2) = - exp(2h/L)
u(x) =U0 / ( 1- exp(2h/L) ) [ exp(x/L) - exp(2h/L) exp(-x/L) ]
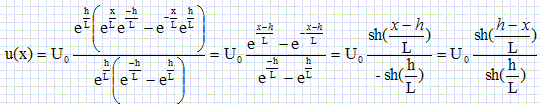
i = - 1/r du/dx =U0 ch((h-x)/L) / (rL sh(h/L) ).
u(0) = U0 ; i(0) =U0 coth (h/L) / (rL) ; Rcc0 =r L / coth (h/L) = rL th (h/L)
h/L <<1 ; th (h/L) ~ h/L ; Rcc0 ~r h =0,01 W.
Exprimer
puis calculer la
puissance Pcc consommée
dans le câble. Commenter.
dp = u(x) i (x) =-1/ r u(x)du(x) /dx = -1/(2r) d(u2(x)) ; intégrer entre 0 et h :
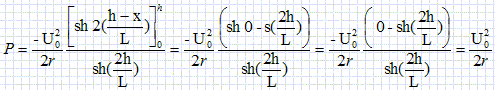
La puissance est perdue par effet Joule.
On
considère un conducteur cylindrique homogène de grande
longueur, de rayon R, parcouru par un
courant axial homogène d’intensité constante I. Le
courant circule dans le sens des z croissants.
Soit
z’z l’axe de symétrie. On utilisera
la base de vecteurs unitaires (voir figure 3).
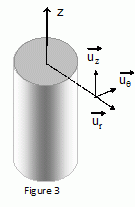
Exprimer
la densité
de courant dans le
conducteur.
La densité de courant est
j=I/(pR²),
R rayon du câble.
Quelle
est
l’orientation du champ magnétique créé par le courant ?
Les vecteurs sont écrits en gras et en bleu.
L'axe
Oz est axe de symétrie du système ; une rotation autour de cet axe ne
modifie pas le champ : la variable q n'intervient donc pas
dans l'expression du champ.
Toute translation le long de l'axe Oz, ne modifie pas le champ : la variable z
n'intervient donc pas dans l'expression du champ.
Tout plan
contenant l'axe Oz est plan d'antisymétrie : le champ appartient donc
au plan contenant l'axe Oz et le point M d'où : Bq( r, z) =0.
Le champ est orthoradial : B(M) = B( r, t) eq.
Exprimer
le champ
magnétique à la distance r de l’axe en
fonction la norme j du vecteur densité de courant, de r, de la perméabilité µo du
vide et d’un vecteur unitaire. On distinguera deux régions de l’espace
et on
introduira la norme j du vecteur
densité de courant.
point intérieur
au câble
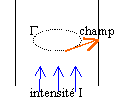
En tout point de G le
champ magnétique a même module et est
tangent à G.
appliquer le th. d'Ampère sur le contour
G, cercle de rayon r,
l'intensité des courants enlacés par
G étant
I
r²/R²
B
2p
r =m0
I
r²/R²
B
=m0
I r / (2p
R²) =m0 j r / 2.
point extérieur
au câble
appliquer le th. d'Ampère sur le contour
G, cercle de rayon r,
l'intensité des courants enlacés par
G étant
I
B
2p
r =m0
I
B
=m0
I / (2p
r) =m0 jR2 /(2r).
si r =R on peut constater
que le champ magnétique donner par les deux
expressions ci dessus a la même valeur.
Continuité du champ magnétique lors
du passage du conducteur au
vide.
|
On
considère maintenant un gaz constitué de protons qui
s’écoule en formant dans le vide un faisceau cylindrique d’axe de
symétrie z’z et de rayon R. Les
protons circulent dans le sens des z croissants. La
densité de courant j est
constante.
Les vecteurs sont écrits en gras et en bleu.
Un
volume élémentaire
dt
de gaz est soumis à la force magnétique : dFm = j ^ B dt.
Exprimer cette force en
fonction de la norme j du vecteur densité de courant,
de la
distance r à l’axe, de dt,
de la perméabilité µo du vide, et d’un vecteur unitaire.
Quel
est l’effet des forces
magnétiques sur le faisceau ?
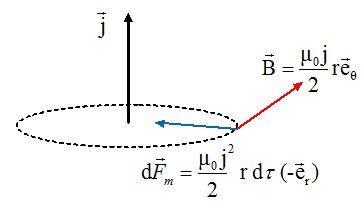
Sous l'effet des forces magnétiques le faisceau à tendance à imploser.
En
régime permanent, le faisceau est en équilibre sous
l’effet conjugué des forces magnétiques et des forces de pression. La
force
due à la pression P qui s’exerce
sur un volume élémentaire
dt s’écrit :
dFP = -grad P dt.
Établir
l’équation
différentielle que satisfait la pression.
dFP + dFm = 0 ; -½µ0j2 r dt-dP/dr dt = 0
½µ0j2 r = -dP/dr ; dP = ½µ0j2 r dr = ¼µ0j2 d(r2)
Intégrer
cette
équation ; en déduire la pression P0
sur l’axe.
Intégrer : P= ¼µ0j2r2 + Cste.
Soient
n le
nombre de protons par unité de volume, v
la vitesse d’un proton et e la charge
d’un proton.
Exprimer
la norme j du vecteur densité de courant en
fonction de n, e et v.
j = n e v.
Calculer
la pression P0 avec les données
suivantes :
µ0 = 4 p 10-7
H m-1 ; n = 1021 m-3 ; e = 1,6 10-19 C
; v = 1,0 105 m/s ; R = 1,0 m.
|