On place une source ponctuelle
S monochromatique de longueur d’onde l
à une distance e d’un miroir plan.
Données :
e = 0,50 mm ; f' = 1,00 m ; l
= 0,60 µm.
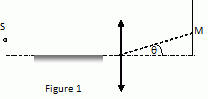
Placer l’image S’
de S donnée par le miroir.
L'image S' est symétrique de S par rapport au plan du
miroir.
On
place une lentille convergente de distance focale f’ comme indiqué sur
la figure et un écran dans le plan focal image de la lentille.
Tracer les deux
rayons issus de S et de S’ qui
arrivent en un point M de l’écran de cote
OM=x comptée à partir
du plan contenant le miroir.
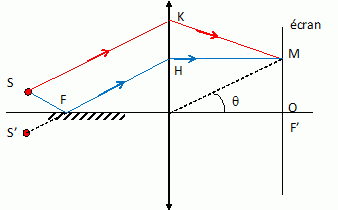
Les deux rayons
interfèrent-ils ? Justifier.
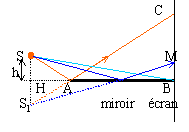
La lumière réfléchie semble provenir de
S', image de S par le miroir plan, symétrique de S par rapport au plan
du miroir.
Sur l'écran il se forme des interférences entre le faisceau issu
directement de S et le faisceau réfléchi par le miroir.
C'est un dispositif à division de
front d’onde.
Les sources S et S' sont cohérentes mais pas synchrones : la réflexion
introduit un déphasage de p.
Les sources sont en opposition de phase.
|
Exprimer
la différence de marche
d
entre les deux rayons.
Différence de marche géométrique : 2 q
x avec tan q ~ q ~ e / f'.
Tenir compte du phénomène de réflexion qui introduit une différence de ½l.
d = 2
e x/f'
+ ½l.
|
En
déduire le déphasage j entre
les deux ondes puis l’ordre d’interférence p au
point M sachant
que la réflexion introduit un déphasage supplémentaire égal à p.
Le déphasage est égal à : j
= 2p/l d = 4p e
x/ (
l
f'
) + p.
Ordre d'interférence p = d / l =
2
e x/ (f'
l) + 0,5.
On
observe des franges rectilignes sur l’écran, parallèles au plan du
miroir. Exprimer
puis calculer
l'interfrange i.
ordre 1 : 1 = 2
e x1/ (f'
l) + 0,5 ; x1
= 0,25 f' l / e ;
ordre
2 : 2 = 2
e x2/ (f'
l) + 0,5 ; x2
= 0,75 f' l / e ;
i = x2
- x1
= f' l / (2e).
i = 1,0 * 0,60 10-6 / 10-3 =6,0 10-4 m.
Soit a
l’amplitude de l’onde
incidente sur le miroir ; l’amplitude de l’onde réfléchie s’écrit
alors : ra. Dans cette expression
r est une constante réelle
positive inférieure à l’unité.
Montrer qu’on peut
écrire l’amplitude complexe de l’onde résultante en M sous la forme :
Nombre complexe associé à l'onde incidente A1 = a ;
Nombre complexe associé à l'onde réfléchie : A2 = ra
exp(jj) ;
Nombre complexe associé à l'onde résultante :
A1 + A2 = a +
ra exp(jj) ;
A =a(1+r exp(jj)).
En déduire que
l’intensité lumineuse en M s’écrit
: I = Imax (1+r2+2r cosj) / (1+r)2.
Pour une onde monochromatique plane, l'intensité est proportionnelle
au carré du module de l'amplitude complexe de l'onde :
A =a (1+ r ( cos j + j sin j))
|A |
=I = a2 [ (1+r
cos j)2
+ ( r sin
j)2]
=a2[1 + 2r
cos j
+ r2
cos2j
+ r2
sin2j
]
;
I = a2
(1+r2+2r cosj ) ;
L'intensité est maximale si cosj
=1
; Imax = a2 (1+r)2.
Par suite I
= Imax (1+r2+2r cosj) / (1+r)2.
|
Soit
Imin l’intensité minimale. Exprimer le contraste C défini par la relation :
C = (Imax -Imin) / ( Imax +Imin )
L'intensité est minimale si cosj
=0
; Imin = a2
(1+r2) ; Imax = a2 (1+r)2.
Imax -Imin= 2 a2r ; Imax +Imin =2a2 (1+ r + r2) ;
C = r / (1+ r + r2)
Calculer
sa valeur sachant que r=0,50.
C =0,5 / (1 +0,5 +0,25) =0,286 ~0,29.
|


