plan
incliné.
Un solide de masse m glisse sur un plan
incliné d’un angle a au
dessus de l’horizontale. Sa trajectoire
est dirigée suivant la ligne de plus grande pente. Au passage au point
A, sa
vitesse est VA = 2,00 m/s. Au passage au point B, sa vitesse
est VB
= 2,83 m/s. Il existe un frottement solide, la force de frottement a
une valeur
constante.
Données :m = 200 g ; AB = 50 cm ; a = 30° ; g = 10 ms-2.
Cos 30
= 0,87 ; sin 30 = 0,5 ; 2,832 ~ 8.
A-
La direction du vecteur accélération du
solide
est verticale. Faux.
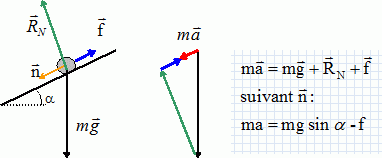
B-
La
valeur de l’accélération du solide est égale à 1 m s-2. Faux.
V2B-V2A=
2 a AB ; a = (V2B-V2A)
/
(2AB) = (2,832-22) / 1 =8-4 = 4 m s-2.
C-
La valeur de la force de frottement est
égale à
f = 0,2 N. Vrai.
f = m(g sin 30-a) =0,2(10*0,5-4) = 0,2 N
D-
Du fait de la force de frottement, le solide
finira par s’arrêter. Faux.
La vitesse du solide augmente entre A et B.
|
Freinage.
Un véhicule de masse m = 1,25 t, lancé
à la vitesse v = 25
m/s ( 90 km/h) parcourt avant de s’arrêter un distance qui est fonction
du
coefficient d’adhérence k des roues. Ce coefficient est défini par k =
f/ P
avec P : poids du véhicule et f force de freinage maximale
Sur route sèche k1
=0,6 ; sur route humide k2=0,2 ; le temps de
réflexe du
conducteur est 0,5 s.
Données : 25*25 =
625 ; 625 / 12 ~52 ;
g = 10 ms-2..
A-
Le
conducteur utilise la force de freinage maximale. En tenant compte du
temps de
réflexe du conducteur, la distance maximale parcourue par la voiture
sur route
sèche avant de s’immobiliser est de ‘ordre de 65 m. Vrai.
Ecrire le th. De l’énergie cinétique ( sur route horizontale, le poids
et l’action
normale du plan, perpendiculaires à la vitesse, ne travaillent pas )
0-½mv2= -kmg d avec d :
distance de freinage
d = 0,5 v2/(kg) = 0,5*625/ (0,6*10) =625 / 12 ~52 m
Prendre en compte le temps de réflexe durant lequel la voiture parcourt
25*0,5
= 12,5 m.
Sur route mouillée cette distance est multipliée par 3. Faux.
d = 0,5 v2/(kg) =
0,5*625/ (0,2*10)
=625 / 4 ~156 m puis ajouter 12,5 m.
B-
On suppose que le conducteur n’utilise
pas la
force de freinage maximale. Le véhicule s’arrête après un parcours de
75 m dur
route sèche. La valeur de l’accélération est 2,5 m s-2. Faux.
75-12,5 = 62,5 m puis : V2B-V2A=
2 a AB ; a = (V2B-V2A)
/
(2AB) = (02-252) / 125 =-625/125~-5 m s-2.
Dans les conditions précédentes f = 6250 N. Vrai
Ecrire la seconde loi de Newton sur un axe horizontal orienté dans le
sens du
mouvement :
ma = -f ; f = 1250*5 = 6250 N.
|
Satellite.
Un satellite artificiel de la Terre,
assimilable à un solide
ponctuel, décrit une orbite circulaire dans le plan de l’équateur
terrestre. Le
centre de la trajectoire coïncide avec le centre de la Terre. Ce
satellite
comme la Terre, tourne d’est en ouest. La période de révolution du
satellite
est T.
Sur route sèche k1
=0,6 ; sur route humide k2=0,2 ; le temps de
réflexe du
conducteur est 0,5 s.
Données : altitude du satellite
par rapport au
sol : h = 640 km ; rayon de la Terre R = 6400 km ;
valeur de la
pesanteur au sol g0 = 9,8 m s-2. R+h ~R+0,1 R.
A-
Le mouvement du satellite est uniforme. Vrai.
Il faudrait préciser que
le référentiel d’étude est le référentiel géocentrique.
B-
Si l’altitude du
satellite double, sa
période de révolution serait alors T 2/3. Faux.
Ecrire la 3è loi de Kepler : T2/(R+h)3
= T2/(1,1R) 3 =constante
Si l’altitude double, la période est notée T’ : T’2 /
(R+2h)3
= T’2 / (1,2R)3
C-
La
vitesse du satellite sur sa trajectoire est : v = (1,1 R/g0)0,5.
Faux.
v = ( GM/(1,1R))0,5 ; avec GM = g0R2
d’où
v = (g0R/1,1)0,5.
D-
La
période du satellite est supérieure à une heure. Vrai
Le satellite décrit une circonférence ( 2 p
*1,1 R ) en T seconde à la vitesse v = (g0R/1,1)0,5.
2 p *1,1 R = vT = (g0R/1,1)0,5T ;
T = 6,28*1,1*6,4 106 / (9,8*6,4 106/1,1)0,5 ~6000
s.
Trajectoire
circulaire.
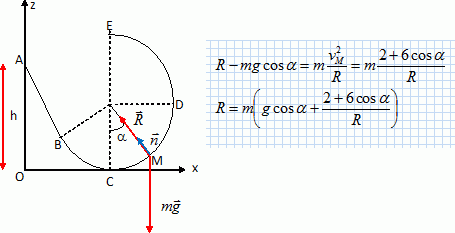
|
Un solide
pratiquement ponctuel, de masse m = 100 g se déplace sans frottement le long de
la piste ABCDE. AB est une gouttière rectiligne, inclinée d’un angle q = 60° sur le plan horizontal. L’altitude du
point A est h = OA = 0,40 m. BE est une portion de cercle de rayon R = 30 cm.
Le solide est lâché sans vitesse initiale du point A. prendre g = 10 m s—2.
A. Le solide atteint le point E. Faux.
Ecrire la
conservation de l’énergie mécanique en A et en E.
mgh = mg*2R +½mv2 ; v2 = 2g(h-2R) ; or h est
inférieur à 2R et v2 est positif.
B. En C la vitesse linéaire du
solide est 5,0 m/s. Faux.
Ecrire la
conservation de l’énergie mécanique en A et en C.
mgh = ½mv2 ; v = (2gh)0,5 = (20*0,40)0,5
=2,8 m/s.
C. Au point M, la vitesse linéaire du
solide est v = (2+6 cos a)0,5.
Vrai.
Altitude de M par
rapport à O : R(1-cos a)
Ecrire la
conservation de l’énergie mécanique en A et en M.
mgh = ½mv2 + mgR(1-cos a) ; v = (2gh -2gR(1-cos a) )0,5 =(20*0,4-20*0,3
+20*0,3cos a) )0,5 .
D. Au point M la réaction
de la piste est R =m( g cos a + 2 + 0,6
cos a). Faux.
|

