Diffraction
par une fente.
On
observe sur un écran la figure de diffraction ci-jointe d’un faisceau
laser de longueur d’onde l
par une fente de largeur a et de longueur b située à la
distance L de l’écran.
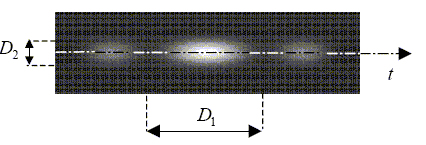
- L’axe t est colinéaire à la
direction longitudinale de la fente. Faux.
Si la fente est
verticale, la figure de diffraction est horizontale.
-
Quelle que soit la largeur de la fente, on observe une figure de
diffraction du même type. Faux.
la
largeur de la fente doit être de l'ordre de grandeur de la longueur
d'onde de la lumière utilisée, sinon il n'y a pas de
diffraction.
- L =
D1 dépend de l. Vrai.
- L = D1 dépend de la largeur de la fente. Vrai.
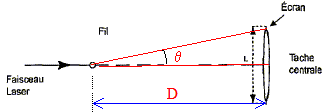
tan q =
½L/D voisin de q radian
pour les angles petits.
d'autre part q = l/a.
avec : l longueur d'onde
(m) et a : diamètre du fil (m)
en tenant compte des deux relations ci-dessus : ½L/D=l/a soit a=2lD/L ou L = 2l D/a.
- D2 dépend de
la longueur de la fente. Faux.
Propagation d'une onde.
Une onde se propage, de la gauche vers
la droite, le long d’une corde supposée infinie.
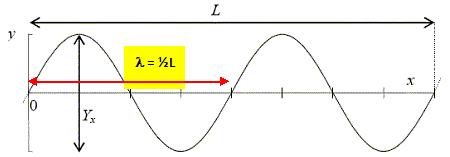
La figure ci-dessous représente la corde à un instant t = 0 pris pour
origine du temps :
|
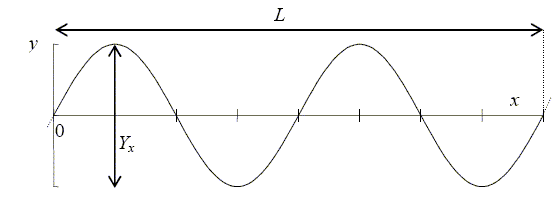
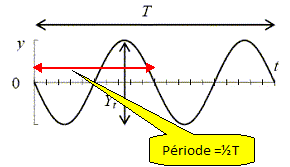
La figure ci-dessous représente l’allure de y (t ) pour le point O ( x
= 0 ) :
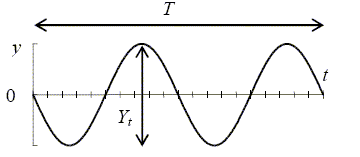
|
- L’ onde
est longitudinale. Faux.
L'onde
est transversale : la déformation du milieu est perpendiculaire
à la direction de propagation de l'onde.
-YX
= Yt. Vrai.
- La longueur
d’onde vaut L/ 4.
Faux.
- La
fréquence vaut 1/ 4 T) . Faux.
fréquence = 1 /
période = 1/ (0,5 T) = 2/T.
- La
célérité vaut L/T.
Vrai.
célérité = longueur d'onde / période
=0,5 L / (0,5 T) = L/ T.
Effet
Doppler.
Une
source S émet un bip à la période T en se déplaçant à la vitesse vS
vers un observateur immobile situé en O.
Le bip se propage à la célérité c et S émet son premier bip à l’instant
t = 0 . La distance OS initiale est notée d.
- O reçoit le premier
bip à la date t1 = T. Faux.
t1 = d/c.
- Lorsque S émet le deuxième bip, la source se trouve à la distance d-vST
de O. Vrai.
- O reçoit le deuxième bip à la date t2 = 2T. Faux.
t2 =T+(d-vST) / c.
- O reçoit le troisième bip à la date t3
=( d -2vST) / c. Faux.
t3 =2T+(d-2vST) / c.
- La période des bips reçus par O est égale à celle des bips envoyés
par S.
Faux.
la période
des bips recçu est : t2-t1
= t3-t2 =T-vST) / c.
|
Propagation d'une onde.
Un vibreur installé au centre O d’un bassin produit une onde à la surface de l’eau.
On note r la coordonnée radiale d’un point de la surface de l’eau et z la cote, coordonnée verticale. On écrit :
z(t) =z0 cos [6,28 (at-br) + p/3]
z0 est une constante, t s’exprime en seconde et r en mètre.
a et b sont des constantes telles que a =1 s-1 et b =1 m-1 .
- l'onde est transversale. Vrai.
La déformation de l'eau est verticale ; l'onde se propage dans toutes les direction à la surface plane de l'eau.
- La célérité de l'onde vaut 1 m /s. Vrai.
Chaque point de la surface reproduit le mouvement de la source avec un retard q = r/c.
z(t) =z0 cos [w (t-q) + f ]
On identifie at-br à t-q = t - r/c d'où 1/c =b/a ; c = a/b =1 m s-1.
- La période vaut T = 1 s. Vrai.
w = 6,28 rad/s ; w =2 p/ T ; T = 1 s.
- La longueur d'onde vaut l = 1 m. Vrai.
l = c T = 1*1 = 1 m.
- Un point de la surface de l’eau situé à 1 m de O est en phase avec O. Vrai.
Deux points distants d'un nombre entier de longueur d'onde vibrent en phase. |





