Pourquoi
éteindre les phares quand le moteur est arrêté ?
Etude d’un circuit simplifié des phares d’une
voiture électrique.
Le circuit des phares d’une voiture électrique doit respecter les
conditions suivantes :
- Les phares peuvent être allumés même si le moteur est éteint (et
inversement).
- Si un phare ne fonctionne plus, l’autre doit encore être allumé.
- On commande l’allumage et l’extinction des deux phares en même temps.
- On commande la mise en route et l’arrêt du moteur indépendamment des
phares.
Parmi les
circuits suivants, choisir celui qui remplit les conditions énoncées
cidessus.
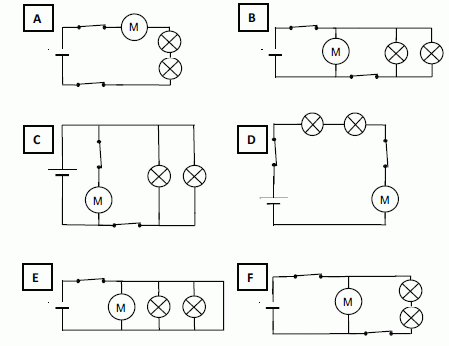
Les deux phares doivent être montés en dérivation : A, D et F ne
conviennent pas.
Les phares peuvent être allumés même si le
moteur est éteint : E ne convient pas.
On commande la mise en route et l’arrêt du
moteur indépendamment des phares : C
convient.
|
Etude
du circuit électrique permettant d’utiliser les essuie-glaces sur une
durée réduite (par exemple lors du lavage du pare-brise)
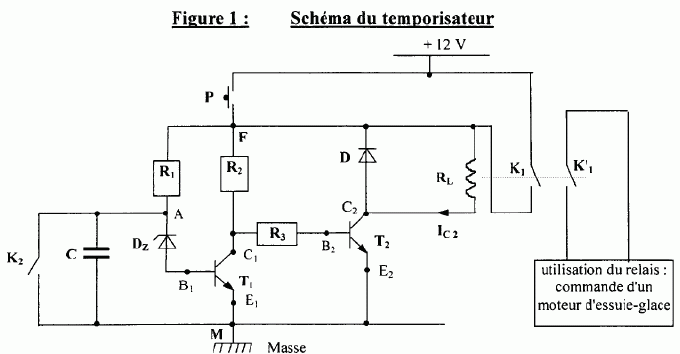
Le montage ci-dessous est destiné à commander un relais possédant deux
interrupteurs K1 et K’1. L’interrupteur K1
fait partie du circuit de temporisation et l’interrupteur K’1
commande l’utilisation du relais. Le montage est mis sous tension à
l’aide d’un bouton-poussoir P.
|
Ce circuit
comporte un condensateur C, une diode D, une diode Zener DZ,
un relais,
des résistors et deux transistors bipolaires T1 et T2.
Avant la mise sous tension, le condensateur est déchargé et les
interrupteurs K1, K1’ et K2 sont
ouverts.
Etude
de la charge du condensateur.
On considère le circuit ci-dessous. A t = 0 s, l’interrupteur est
fermé. Le condensateur est initialement déchargé.
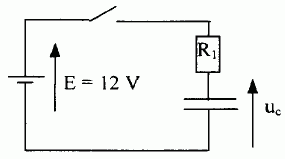
Etablir l’équation
différentielle à laquelle obéit la tension aux bornes du condensateur uC(t).
Additivité des tensions : E = R1 i + uC avec i =
dq/dt =CduC/dt.
E = R1CduC/dt + uC.
Les solutions de cette équation différentielle sont du type : uC(t)
= k1 . e-kt + k2 où k, k1
et k2 sont des constantes.
Donner
l’expression de uC(t) dans les
conditions de l’expérience.
à t=0, uC(0) = 0 = k1+ k2 ; à t suffisamment grand uC=
E = k2 , par suite k1=
-E.
uC(t) =E(1- e-kt
) avec k = 1/(R1C).
La courbe de charge du condensateur à travers la résistance R1
est donnée cidessous :
Déterminer
graphiquement la constante de temps notée τ du dipôle R1C.
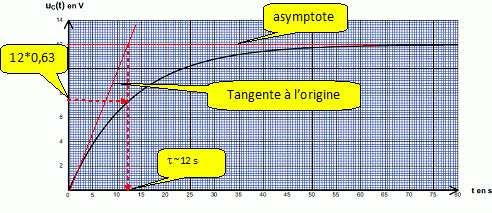
Déterminer
la durée nécessaire pour obtenir une tension uC égale à 6,3 V.
uC(t) =E(1- e-kt )
; 6,3 = 12 (1-exp(-t/12)) ; ln (12/6,3) = t/12 ; t = 12 ln(12/6,3) =7,7 s.
Etude de la
diode Zener.
La
caractéristique de la diode Zener, supposée parfaite, est représentée
ci-dessous :
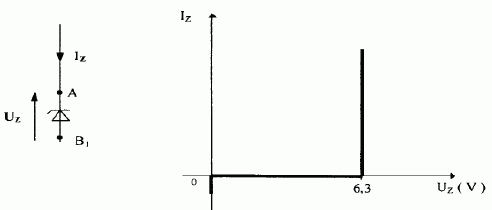
Indiquer
la convention choisie pour la représentation symbolique de la tension UZ et de l'intensité IZ.
Convention récepteur : la diode est montée en inverse.
Déterminer
la tension à partir de laquelle la diode Zener est passante.
Montée en inverse, la diode Zener devient passante à partir de la
tension UZ = 6,3 V.
Le circuit ci-dessous permet d'étudier le rôle de la diode Zener dans
le circuit de commande des essuies-glaces :
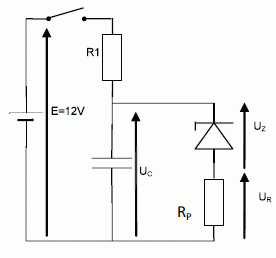
A t = 0, l'interrupteur est fermé ; le condensateur est déchargé.
Indiquer
la valeur des tensions uC, uZ et uR à t = 0 s et à t =
5 s.
A t = 0 : la
continuité de l'énergie stockée par le condensateur conduit à uC(0-)
= uC(0+)=0.
uC = uZ + uR =0.
La diode Zener est non passante ( i = 0) et en conséquence la tension uR
=Ri est nulle ; par suite uZ = 0.
A t = 5 s : uC(t) =E(1- e-kt = 12
(1-exp(-5/12) =4,1 V.
uC = uZ + uR
.
La diode Zener est non passante ( i = 0) et en conséquence la tension uR
=Ri est nulle ; par suite uZ =
4,1 V.
Indiquer,
à quel moment, la résistance RP est traversée par
un courant.
La diode Zener doit être passante : uZ = 6,3 V.
Dès que uC = 6,3 V, la
résistance RP est traversée par un courant. le calcul
ci-dessus donne t = 7,7 s.
Indiquer
la valeur des tensions uC, uZ et uR à t = 11 s.
uC(t) =E(1- e-kt =
12 (1-exp(-11/12) =7,2 V.
La diode Zener est passante : uZ = 6,3 V.
uC = uZ + uR donne
uR = 7,2-6,3 = 0,9 V.
Etude du relais
électromagnétique.
Le
relais électromagnétique est composé d'une bobine comportant un noyau
de fer doux (partie commande), et d'un contact ayant une position "
repos ", et une position " travail".
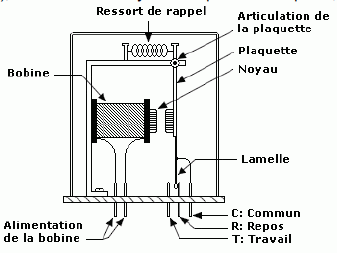
La bobine est parcourue par un courant . Quel phénomène
provoque la fermeture des interrupteurs K1 et K'1 ?
Une bobine traversée par un courant se comporte comme un aimant. Le
contact est attiré par le noyau de fer doux et passe en position
"travail".
Expliquer
comment le contact revient en position repos lorsque l'on coupe le
courant.
La bobine cesse d'être un aimant dès que l'intensité du courant
s'annule ; le noyau de fer doux n'attire plus le contact ; ce dernier
est rappellé vers la position "repos" par le ressort.
|
Etude des
transistors.
Le
circuit de la figure 1 comporte deux transistors bipolaires de type
NPN. Ce type de transistor est schématisé de la façon suivante :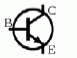
B représente la base, C le collecteur et E représente l’émetteur.
Les deux transistors sont identiques et fonctionnent en commutation.
En commutation, un transistor est commandé par le courant de base iB
:
- si iB = 0 le transistor est bloqué, il se comporte alors
comme un interrupteur ouvert entre le collecteur et l’émetteur, les
courants au collecteur et à l’émetteur sont alors nuls.
- si iB > 0 le transistor est saturé, il se comporte
alors comme un interrupteur fermé entre le collecteur et l’émetteur, la
tension VCE est très faible et, ici, la tension
base-émetteur VBE est égale à 0,7 V.
On enfonce le bouton-poussoir P pour entraîner la fermeture de K1
et de K’1 puis on le relâche.
Le
transistor T1 étant bloqué,
expliquer pourquoi le transistor T2
devient saturé.
T1 se
comporte alors
comme un interrupteur ouvert entre le collecteur et l’émetteur ; le courant de base iB 2 est
positif et le transistor T2 est saturé.
Le circuit peut être schématisé comme sur l’annexe 1 (en tenant
compte de l’état des 2 transistors).
Repasser,
à l’aide d’un stylo de couleur, les branches parcourues par un courant
non nul,
au moment où l’on appuie sur le bouton poussoir.

En déduire, alors,
l’état des interrupteurs K1 et K1’.
La bobine du relais est traversée par un courant, le contact passe sur
la position travail, fermant les interrupteurs.
Expliquer
pourquoi la tension UAM augmente puis se
stabilise à
7 V.
Le condensateur se charge et la tension à ses bornes augmente ; quand
elle atteint 6,3 V, la diode Zener devient passante et la tension aux
bornes de la diode Zener vaut alors 6,3 V.
Le courant dans la base du transistor T1 n'est plus nul et T1
est saturé : UBE = 0,7 V.
UAM=UAB1+UB1E1=
6,3 + 0,7 =7 V.
Expliquer les
changements de mode de fonctionnement des deux transistors, lorsque UAM
vaut 7 V.
T1 est saturé et se comporte comme un interrupteur fermé ; en conséquence iB2 est nul et le transistor T2 est bloqué.
En déduire alors l’état des interrupteurs K1 et K1’.
T2 étant bloqué ( interrupteur ouvert ) la bobine du relais
n'est traversé par aucun courant : le contact passe sur la position
repos.
On appelle « durée de temporisation » le temps nécessaire pour
que la tension UAM atteigne la valeur de 7 V.
Déterminer la durée de temporisation de ce disposiitif.
La tension aux bornes du condensateur atteint la valeur 6,3 V en 7,7 s.
Comment peut-on agir pour augmenter la durée de temporisation
du montage ?
Il faut augmenter la constante de temps RC du condensateur : augmenter R ou C ou R et C.
|
|








