Comment peut-on
décrire le mouvement d'un véhicule ?
Proposer
une définition d'un référentiel galiléen.
Dans un référentiel galiléen, la première loi de Newton (
ou principe d'inertie ) s'applique.
La
voiture roule, sur une route rectiligne horizontale, à la vitesse
constante de 10 km/h. Au passage d’une marque, un chronomètre est
déclenché, le conducteur débraye et maintient la
direction, le véhicule s’arrête après avoir parcouru une distance de
31,2 m.
Préciser la nature
du mouvement du véhicule après le passage de la marque. Justifier la
réponse.
Le mouvement reste rectiligne, la vitesse diminue jusqu'à
s'annuler : le mouvement est rectiligne uniformément décélléré.
On
considère que la force de frottement aérodynamique est négligeable
devant la résistance au roulement (force de frottement solide).
C'est
la résistance des roulements du véhicule. La propriété des frottements
solides est d'avoir une valeur constante indépendante de la vitesse. En
revanche, les frottements solides sont proportionnels à la masse
du véhicule. On a ainsi la relation :
Fs
= m.g.k ; m = masse totale du véhicule (masse à vide + masse du
conducteur…) ; g = 9,81m/s² ; k = coefficient de frottement solide.
En utilisant le
théorème de l’énergie cinétique, calculer le coefficient de résistance
au roulement k (coefficient de frottement solide).
Le
poids du véhicule et l'action normale de la route, perpendiculaires
à la vitesse ne travaillent pas ; seule la force de
frottement solide travaille : W = - mgk AB avec AB = 31,2 m
Théorème de l'énergie cinétique entre A ( passage devant la marque ) et
B (arrêt).
0-½mv2 = W = -mgk AB ; v = 10 / 3,6 = 2,78 m/s ;
k = ½v2/ (gAB )= 0,5*2,782 / (9,81*31,2
)=1,26 10-2 ~1,3 10-2.
Calculer
la valeur de la force de frottement solide. On prendra 70 kg
pour la masse du conducteur ; masse de la voiture 1214 kg.
Fs = mgk = (1214+70)*9,81*1,26 10-2 ~158,7 ~1,6 102 N.
Calculer
la valeur de la force de frottement aérodynamique,
Surface de trainée 0,580 m2.
Force
de frottement aérodynamique (Fa)
Cette
force se manifeste à grande vitesse : un vent fort pousse davantage
qu'un vent faible. Dans le domaine automobile, les vitesses et
l'aérodynamisme font que les frottements aérodynamiques sont
proportionnels
au carré de la vitesse v. Ils sont aussi proportionnels à la densité de
l'air ρ, à la surface frontale S du véhicule et à son aérodynamisme
propre Cx. On a ainsi la relation :
Fa = 1/2.ρ.S.Cx.v² ; ρ = masse volumique de l’air = 1,2 kg/m3
(à 20°C)
S est la surface frontale en m² = surface projetée dans le plan
orthogonal au vecteur vitesse.
Cx décrit l'aérodynamisme propre (coefficient de traînée).
La vitesse se mesure en m/s. C'est le paramètre que le conducteur fait
varier !
Fa =
1/2.ρ.S.Cx.v² ρ =0,5 *1,2*0,580*2,782 =2,7 N.
Cette force est bien négligeable devant la force de frottement solide.
|
Déterminer
l’équation horaire de ce mouvement.
Calculer le temps mis par le véhicule pour parcourir les 31,2 mètres.
Ecrire la seconde loi de Newton sur un axe horizontal orienté dans le
sens du mouvement :
-Fs = ma ; -mgk = ma ; a = -gk = -9,81 *1,26 10-2 =
-0,1236 ~ -0,12 m s-2.
v = -at + v0
; x =-½at2+v0t avec v0 = 2,78 m/s
t = -v0 / a = 2,78 / 0,1236 =22,47 ~ 22 s.
|
Exploitation
du film 2 du document ressource : la voiture roule à la vitesse
constante de 100 km/h.

A cette
vitesse, on considère que :
- le moteur consomme 5 L de carburant au 100 km ;
- la valeur de la résultante des forces de frottement est égale à 427 N.
On souhaite exploiter le film 2, dans le cadre de l’étude d’un
mouvement rectiligne uniforme.
Quelle(s)
indication(s) doit-on fournir aux élèves pour une exploitation de ce
film à l’aide d’un logiciel de chronophotographie ?
Il faurt une échelle des distances : indiquer la distance réelle
entre le premier et le dernier poteau blancs, situés en arrière
plan.
Il faut une échelle des temps : indiquer la durée entre deux photos.
Déterminer
la force de traction nécessaire pour maintenir la voiture à cette
vitesse. Justifier la réponse.
Le mouvement est rectiligne uniforme : le principe d'inertie indique
que la somme vectorielle des forces appliquées à la voiture est nulle.
La voiture est soumise à son poids, à l'action normale de la route,
opposée au poids. La force motrice est donc opposée à la force de
frottement.
Valeur de la force de traction motrice : 427
N.
Déterminer
la puissance mécanique nécessaire, à chaque instant, au mouvement.
Puissance (W) = force motrice (N) * vitesse (m/s) = 427*100/3,6 = 1,186
104 W ~11,9 kW.
Calculer
l’énergie théorique nécessaire pour parcourir 100 km.
Energie (J) = puissance (W) * durée (s) = 1,186 104
*3600 =4,27 107 J.
Cette
énergie est produite grâce au pouvoir calorifique du carburant (gazole).
Calculer
l’énergie qui peut être cédée sous forme thermique par la combustion de
5 L de gazole.
Pouvoir calorifique du gazole : Pcg= 44,8 MJ. kg-1
; densité gazole : dg= 0,85.
masse de gazole : 5*0,85 =4,25 kg
Energie libérée par la combustion de 5 L de gazole : 4,25 *44,8 =
1,904 102 MJ~1,9 108 J.
Calculer
le rendement thermique du moteur.
4,27 107 / 1,9 108 = 0,224 ( 22 %).
Comment
passer de la vitesse des roues à celle de la voiture ?
A l’aide
des données de la fiche technique du document ressource, montrer que le
diamètre de la roue vaut 621 mm. En déduire la distance parcourue par
le véhicule en un tour de roue.

Diamètre de la jante + 2 hauteur du flanc du pneu = 16*2,54
+2*0,55 *19,5 = 62,1 cm = 621 mm.
Distance parcourue en un tour de roue = circonférence de la roue = pi D
= 3,14 * 0,621 =1,95 m.
Calculer
la fréquence de rotation de la roue lorsque le véhicule roule à 100 km/h.
100 / 3,6 = 27,77 m/s ; fréquence des roues = nombre de tours par
seconde = 27,77 / 1,95 =14,25 ~ 14,3 Hz.
A l’aide
des caractéristiques du moteur du document ressource, calculer, en
précisant la démarche, la fréquence de rotation du moteur lorsque le
véhicule roule à 100 km/h en cinquième.
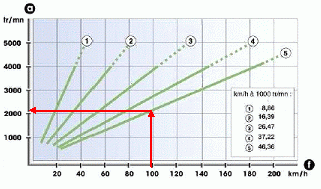
fréquence f ~ 2100 tr/min = 2100 / 60 ~35 Hz
( tr/s)
Le rapport de transmission global est le rapport de la fréquence de
rotation de l’arbre de la roue sur la fréquence de rotation du moteur.
Calculer
le rapport de transmission global lorsque la voiture roule à 100 km/h
en cinquième.
14,3 / 35 = 0,41.
Indiquer
qualitativement comment évolue ce rapport si, à la même vitesse (100
km/h), le conducteur passe la quatrième. Justifier la réponse.
Le graphe ci-dessus indique une fréquence vosine de 3700
tr/min en quatrième à 100 km/h; soit 3700/60 ~ 62 Hz.
Rapport de transmission global dans ces conditions : 14,3 / 62 ~0,23 ;
ce rapport diminue.
Lors d’une séquence pédagogique, on souhaite développer la capacité du
module T2 : « Déterminer expérimentalement une relation entre fréquence
de rotation et
vitesse linéaire ».
Exprimer
cette relation en explicitant chaque grandeur.
Proposer
un dispositif expérimental adapté à cette séquence, et exploitable en
classe.
v = pi D N / 60 ; v : vitesse en m/s ; D : diamètre de la roue en m ; N
: nombre de tours effectués en une minute.
Qu’est-ce
qu’une voiture puissante ?
La valeur du couple moteur varie selon la fréquence de rotation du
moteur.
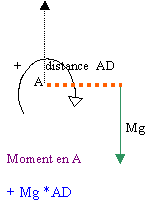
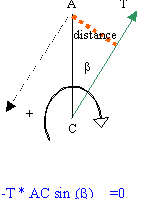
Illustrer, à l’aide d’un schéma, la notion de moment d’un couple
de forces. Annoter ce schéma et donner l’expression littérale qui représente le
moment d’un couple de forces.
Un couple est
constitué de deux forces, ayant des directions
parallèles, des sens contraire, et ayant même
norme. L'effet d'un couple est la rotation ou la
torsion
Pour la 207 HDI, indiquer, à l’aide des « courbes moteur » du
document ressource, une estimation de la fréquence de rotation du moteur pour
laquelle le couple est maximal.
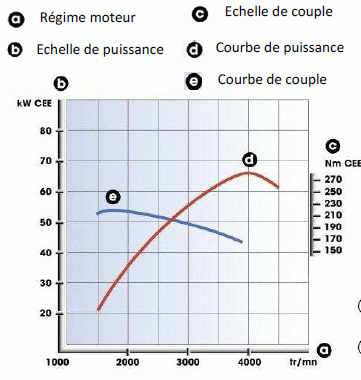
La courbe de couple "e" présente un maximum pour une fréquence voisine de 1800 tr/min.
A l’aide des « courbes moteur » du document ressource :
Déterminer une estimation de la valeur du couple moteur lorsque
la voiture roule à 50 km/h en 2nde vitesse.
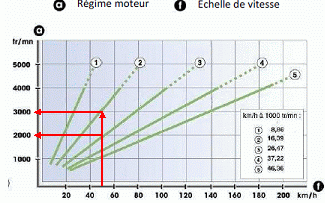
Régime moteur en 2nde à 50 km/h : 3000 tr/min.
Lors d’une phase d’accélération, le conducteur passe de la 2nde
à la 3ème vitesse à 50 km/h, indiquer l’influence de ce changement de vitesse sur
la valeur du couple moteur.
Régime moteur en 3ème à 50 km/h : 2000 tr/min.
Justifier la pertinence de ce changement de vitesse dans cette
situation.
Le moteur tourne moins vite et consomme donc moins de carburant.
On donne la relation P = w MC avec P : puissance en W, w : vitesse angulaire en rad.s-1, MC : moment du couple utile du moteur en N.m.
A l’aide de la caractéristique d’un moteur électrique donnée
dans le document ressource, montrer que P s’exprime en fonction de MC par la relation :
P = 400 pi MC -1000 pi MC2.
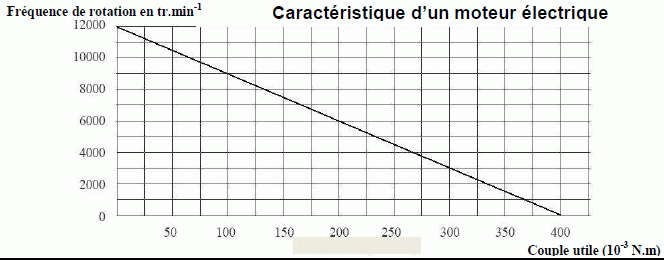
La courbe est une droite ; la fréquence de rotation ( tr/min) est proportionnelle au couple utile ( Nm) :
pente de la droite : -12000 / 0,400 = -30 000 tr min-1 N-1 m-1 ou -30 000/60 = -500 tr s-1 N-1 m-1 ou w = - 1000 pi rad s-1 N-1 m-1.
Ordonnée à l'origine : 12000 / 60 = 200 tr /s = 200 *2 pi rad/s = 400 pi rad/s.
Equation de la droite : w = 400 pi - 1000 pi MC. P = 400 pi MC -1000 pi MC2.
Le professeur propose à ses élèves de déterminer la valeur du
moment du couple utile du moteur correspondant à la puissance maximale.
A quelle notion mathématique du programme de baccalauréat professionnel fait-on appel ?
Une fonction passe par un extrémum lorsque sa dérivée première s'annule.
|
Comment avoir une bonne tenue de route
?
Le volume Va d’air contenu dans un pneu est considéré constant : Va = 21 L.
Déterminer, dans les conditions d’utilisation courante (P = 2,2 bar et t = 20 °C), le rapport PV/T. Exprimer le résultat en J.K-1, arrondi au dixième.
V = 0,021 m3 ; P = 2,2 105 Pa ; T = 273+20 = 293 K.
PV/T = 0,021*2,2 105 / 293 = 15,8 J K-1.
Calculer la pression de l’air contenu dans ce pneu à 0°C.
Le rapport PV/T et v sont constants :
P20 / 293 = P0 / 273 ; P0 = P20 *273 / 293 =2,0 bar.
D'où
la préconisation du constructeur de pneus : « pour compenser l'effet
"basse température" en hiver et rouler à bonne pression, il est
nécessaire de rajouter 0,2 bar(à froid) à la pression d'utilisation
courante ».
|
|