Mesure de températures : thermomètre à dilatation de liquide, thermistance, caplp et cafep 2010.

Les échelles de température. En 1742, l'astronome et physicien suédois Anders Celsius définit une échelle de température, dite échelle centigrade à deux points fixes. Que signifie échelle centigrade ? Les deux points de référence de l'échelle sont distants de 100°. Dans cette échelle l'eau gèle à 0 °C et bout à 100 °C dans les conditions standard de pression. On utilse aujourd'hui une échelle thermodynamique ou absolue définie par dS/dU = 1/T. Que représentent les fonctions thermodynamiques S et U ? S : entropie ; U : énergie interne. Ces échelles sont dites à point fixe. Pour l'échelle Kelvin, quel est le point fixe ? Le zéro absolu est la température  la plus basse qui puisse exister dans l'univers. Elle vaut -273,15 °C. Au zéro absolu  aucune chaleur ne peut être tirée d'un corps. Ce point est indépendant des conditions de pression. Que mesure réellement un thermomètre ? Un thermomètre ne mesure que sa température propre qth. Cette température dépend de la température q du milieu à mesurer, mais elle dépend aussi de la température qex du milieu extérieur ( avec lequel le thermomètre est forcément en contact et des caractéristiques thermiques du thermomètre. Pour deux corps A et B respectivement aux températures qA et qB l'échange de puissance thermique PAB du corps A vers le corps B est régi par l'équation : PAB = (qA -qB ) / RAB où RAB représente la résistance thermique entre le corps A et le corps B. On appellera RM-Th la résistance thermique entre le milieu dont on veut mesurer la température q et le thermomètre, RTH-ex la résistance thermique entre le thermomètre et le milieu extérieur de température qex. Quelle est l'unité d'une résistance thermique ? PAB = (qA -qB ) / RAB  ; RAB   = (qA -qB ) /PAB  ; K W-1. Que peut-on dire de la puissance thermique reçue par le thermomètre et de la puissance thermique transmise par le thermomètre lorsque celui-ci est en équilibre thermique ? La puissance thermique reçue par le thermomètre est éagle à la puissance thermique transmise par le thermomètre, à l'équilibre thermique. En déduire l'expression qF, valeur de qth à l'équilibre thermique en fonction de q, qex, RM-th et RTh-ex. puissance thermique reçue du milieu par le thermomètre :  (q -qF ) / RM-th. puissance thermique transmise à l'extérieur par le thermomètre :  (qF -qext ) / Rth-ex. A l'équilibre thermique : (q -qF ) / RM-th = (qF -qext ) / Rth-ex (q -qF )Rth-ex = (qF -qext )RM-th ; qRth-ex-qF Rth-ex = -qext RM-th +qFRM-th ; qF( RM-th+ Rth-ex ) = qext RM-th +qRth-ex ; qF=(qext RM-th +qRth-ex ) / ( RM-th+ Rth-ex ).   On appelle C la capacité thermique du thermomètre. C'est à dire que la quantité d'énergie thermique élémentaire dQ absorbée par le thermomètre est liée à son élévation de température dqth par la relation :  dQ= Cdqth. Quelle est l'unité de C ? J K-1. En écrivant un bilan d'énergie thermique échangée au niveau du thermomètre pendant une durée élémentaire dt, exprimer l'équation différentielle à laquelle satisfait la température qth. puissance thermique reçue du milieu par le thermomètre :  (q -qF ) / RM-th. puissance thermique transmise à l'extérieur par le thermomètre :  (qF -qext ) / Rth-ex. Puissance absorbée par le thermomètre : Cdqth / dt (q -qth ) / RM-th - (qth -qext ) / Rth-ex=Cdqth / dt q / RM-th + qext / Rth-ex - (1/ Rth-ex+1/ RM-th )qth =Cdqth / dt On pose A = [q / RM-th + qext / Rth-ex  ] / C ; 1/ t = (1/ Rth-ex+1/ RM-th )/ C : dqth / dt +1/ t qth =A. (1) Résoudre cette équation. Le thermomètre est initialement à la température du milieu extérieur et on le plonge brutalement dans le milieu. Solution particulière de (1) : qth = qF ; Solution générale de l'équation sans second membre : qth =B exp (-t/t) avec B une constante. 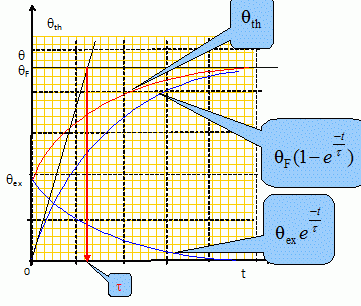Solution générale de (1) : qth = qF + B exp (-t/t)  A t=0 : qex = qF + B exp(0)  ; B = qex - qF ; qth = qF + (qex - qF ) exp (-t/t) ; qth = qF (1-exp (-t/t) + qexexp (-t/t). Thermomètre à dilatation de liquide. Il est constitué d'un réservoir en verre contenant la plus grande partie du liquide, surmonté d'un long tube fin. Le volume V0 du liquide dépend de la température q du liquide. Il est donné par la formule : Vq =Vq0 (1+a(q-q0))  où Vq0 représente le volume du liquide  à la température q0 et a est appelé coefficient de dilatation apparente du couple liquide / réservoir. Que signifie " dilatation apparente du couple liquide/réservoir" ? Ce themomètre utilise le principe de la dilatation apparente d'un liquide dans son enveloppe : à la dilatation du liquide on retranche la dilatation du contenant. Correction de colonne émergente. Les graduations sont données en supposant que l'ensemble du thermomètre est à une même température, mais lors de la mesure de la température q d'un liquide, seule une partie du thermomètre est immergée dans ce liquide.  Une partie se trouvant hors du liquide et à la température ambiante qa, il y a donc lieu de procéder à une correction de colonne émergente. On considère un thermomètre à dilatation de mercure gradué en degré Celsius tel que : V0 : volume du réservoir ; q0 = 0°C ; s : section intérieure du tube  ; d : distance entre deux graduations consécutives. On utilise ce thermomètre pour mesurer la température q d'un liquide. N représente la graduation indiquée par le thermomètre ( niveau du mercure ), n la graduation qui affleure au niveau du liquide. Déterminer en fonction de n, N, s et d le volume du mercure qui est à la température qa. hauteur de la colonne au contact de l'air : (N-n)d  ; volume correspondant : Ve = (N-n)d s. Déterminer le volume qui serait occupé par le mercure de la colonne émergente s'il était à la température q0. Ve =Ve 0 (1+a(qa-q0))  ; Ve 0  = Ve / (1+a(qa-q0)) =(N-n)d s / (1+a(qa-q0)). Déterminer le volume qui serait occupé par le mercure de la colonne émergente s'il était à la température q. V =Ve 0 (1+a(q-q0))  = (N-n)d s (1+a(q-q0)) / (1+a(qa-q0)). En déduire le volume total qui serait occupé par le mercure entier s'il était à la température q. Volume immergé du mercure à la température q : V0(1+a(q-q0)) + nds. Volume total : (N-n)d s (1+a(q-q0)) / (1+a(qa-q0)) + V0(1+a(q-q0)) + nds. Que vaut ce même volume en fonction de N', indication qu'aurait le thermomètre s'il était entièrement à la température q ? volume de la colonne immergée + volume du réservoir : N'd s + V0(1+a(q-q0)). En remarquant que N' (indication) et q ( température) ont la même valeur, en déduire l'expression de q en fonction de n, N, a et qa. (N-n)d s (1+a(q-q0)) / (1+a(qa-q0)) + V0(1+a(q-q0)) + nd s= N'd s + V0(1+a(q-q0)) (N-n)d s (1+a(N'-q0)) / (1+a(qa-q0)) +nd s =N'd s (N-n) (1+a(N'-q0)) / (1+a(qa-q0)) + n =N' q0 =0 ; (N-n) (1+aN') / (1+aqa)  + n= N' (N-n) (1+aN') = (N'-n)(1+aqa) (N-n)  + (N-n)aN' = N'(1+aqa)-n -naqa. N+ (N-n)aN' = N'(1+aqa) -naqa. N' [ 1+aqa-(N-n)a] = N+naqa. N' = (N+naqa) / [ 1+aqa-(N-n)a]. A.N : a = 1,6 10-4 ; °C-1 ; N = 100 ; n=20 ; qa=30°C. N' = (100 + 20*30*1,6 10-4  ) / (1+1,6 10-4*30-80*1,6 10-4) = 100,096 / 0,992 =100,9°C. Utilisation d'une thermistance. On désire mesurer une température variant entre 25°C et 75°C à l'aide d'une thermistance CTN dont on donne la caractéristique ci-dessous : q (°C) 25 30 35 40 45 50 55 60 65 70 75 R(W) 3000 2450 1970 1600 1290 1080 890 740 630 520 444 On utilise le montage en pont de Wheststone suivant : On veut choisir judicieusement les résistanes R1, R2 et R3 de manière  à linéariser l'évolution de V en fonction de la température. Que signifie CTN ? Coefficient de Température Négatif, en anglais NTC, Negative Temperature Coefficient Tracer R = f(q). 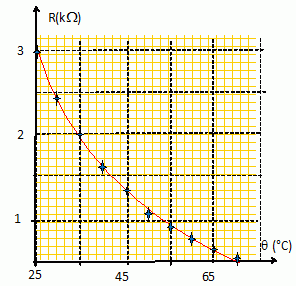Pour linéariser la mesure, on impose V=0 pour q = 25°C, V = 1 V pour q = 50°C et V= 2 V pour q = 75°C. Exprimer V, la tension de séséquilibre du pont. UBD= V = UBC + UCD  ; UBC =R1 i1 ; UCD = -R3 i2 ; E = (R+R1)i1 ; E = (R2+R3)i2 ; V = E[R1 / (R+R1) -R3 / (R2+R3) ]. On appelle a0, a1, a2 les valeurs de R pour 25, 50, 75°C. Donner les 3 relations entre R, R1, R2, R3. 0 =E[R1 / (a0+R1) -R3 / (R2+R3) ] d'où : a0 R3 = R1R2. 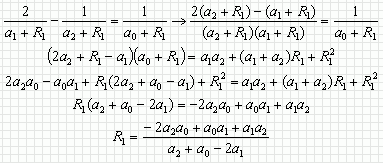1 =E[R1 / (a1+R1) -R3 / (R2+R3) ]  ; 2 =E[R1 / (a2+R1) -R3 / (R2+R3) ] 2E[R1 / (a1+R1) -R3 / (R2+R3) ]= E[R1 / (a2+R1) -R3 / (R2+R3) ] 2R1 / (a1+R1) -2R3 / (R2+R3) = R1 / (a2+R1) -R3 / (R2+R3) 2R1 / (a1+R1)- R1 / (a2+R1) = R3 / (R2+R3) = R1 / (a0+R1) 2 / (a1+R1)- 1/ (a2+R1) = 1 / (a0+R1) A.N : R1 = (-2*3*0,444 +3*1,08+1,08*0,444) / (0,444+3-2*1,08) =0,822 kW. On impose R3=R1. En déduire les expressions et les valeurs de R2 et E. a0 R3 = R1R2 donne :  a0  = R2 = 3,0 kW. 1 =E[R1 / (a1+R1) -R3 / (R2+R3) ] 1 =ER1[1 / (a1+R1) -1 / ( a0+R1) ] 1 =ER1[( a0 -a1 )/ ((a1+R1) ( a0+R1) )] E = (a1+R1) ( a0+R1) / (R1( a0 -a1 )). E = 1,902*3,822 /(0,822 *1,92) =4,6 V. On obtient la courbe suivante : la tension de déséquilibre du pont et la température sont proportionnelles sur l'intervalle 25 °C - 75°C. Amplification du signal. Pour que la tension V soit utilisable, il est nécessaire de l'amplifier. 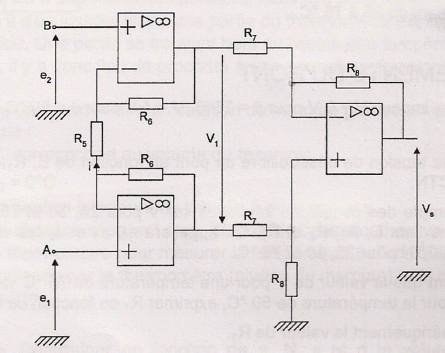Soit le montage suivant : On a e1-e2 = V, tension de déséquilibre du pont de mesure. Exprimer i ( intensité du courant circulant dans R5) en fonction de e1, e2 et R5. Les AO de gauche sont utilisés en régime linéaire ( présence d'une boucle de contre raction entre leur entrée E- et leur sortie) Les entrées de ces deux AO sont au même potentiel : R5 i = e1-e2 = V ; i =( e2-e1) / R5 = V / R5. En déduire l'expression de V1 en fonction de V, R5, R6. Les intensités des courants d'entrée dans les AO sont nulles. (R6+R5+R6) i = V1 ; (2R6+R5) V / R5 = V1. Donner l'expression de Vs en fonction de V1, R7 et R8. Donner l'expression de Vs en fonction de V et des résistances. e1 + R6 i = (R7+R8) i2  ; e2 - R6 i =  Vs + (R7+R8) i1 R8 i2 = Vs +R8 i1  ; Vs =R8 (i2 -i1 ) i2 -i1  = ( e1 + R6 i ) / (R7+R8) -(e2 - R6 i - Vs ) /(R7+R8) i2 -i1  = ( e1 -e2+2 R6 i +Vs) / (R7+R8) Vs =R8( e1 -e2+2 R6 i +Vs) / (R7+R8) Vs(1-R8 / (R7+R8)) = R8( e1 -e2+2 R6 i ) / (R7+R8) Vs(R7 / (R7+R8)) = R8( V+2 R6 i ) / (R7+R8) VsR7= R8( V+2 R6 i ) ; VsR7= R8 V(1+2 R6 / R5) ; Vs= R8 V(1+2 R6 / R5) /R7 . Vs= R8 V(1+2 R6 / R5) /R7 = R8 V1 /R7.

retour -menu