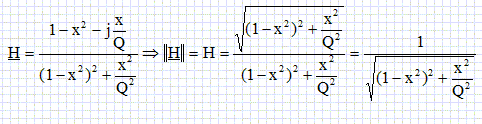Capteur d'humidité, régime sinusoïdal forcé, concours capes interne 2010.

Pour tenir compte de la présence de la vapeur d'eau, il faut connaître l'évolution de l'humidité relative de l'atmosphère en fonction de la température et de l'altitude. On appelle  humidité relative à la température T, le rapport,noté HR et exprimé en %, entre la pression partielle de la vapeur d'eau et la pression de vapeur saturante à la même température T HR(T) = 100 PH2O / Psat H2O(T). Nous allons étudier des dispositifs permettant de mesurer l'humidité relative de l'atmosphère. Ce type de dispositif utilise un capteur constitué d'un condensateur dont la capacité varie avec l'humidité. 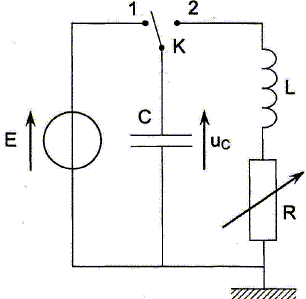Pour mesurer la capacité d'un condensateur, on le place dans le circuit schématisé ci-dessous comprenant une bobine d'inductance L et une résistance R modélisant la résistance totale du circuit. Le générateur fournit une tension E continue. L'interrupteur K est d'abord en position 1. Quelle valeur prend la tension uC ? Le condensateur se charge rapidement et en fin de charge uC =E. A l'instant t=0, on bascule l'interrupteur en position 2. Etablir l'équation différentielle à laquelle satisfait la tension uC(t). On pose l = R/(2L) et w0 =1/(LC)½. Additivité des tensions : uC(t) + Ldi/dt +R i =0 avec i = dq/dt =CduC/dt et di/dt = Cd2uC/dt2. uC(t) + LCd2uC/dt2 + RCduC/dt =0 d2uC/dt2 +R/LduC/dt +1/(LC) uC(t) =0 d2uC/dt2 +2 l  duC/dt +w20 uC(t) =0. Ecrire l'équation caractéristique associée à cette équation. r2 +2 l  r +w20  =0.Pour une valeur de R inférieure à une valeur RC ( appelée résistance critique ), le régime est pseudo-périodique. Exprimer RC en fonction de Let C. Discriminant D =4l2 -4w20  =0 ; l = w0 ; RC/(2L) =1/(LC)½. RC = 2(L/C)½. On se place dans le cas où R < RC. La solution de l'équation différentielle peut alors s'écrire : uC(t) = exp(-lt) (A cos (wt) +B sin(wt)). Donner l'expression de w en fonction de l et w0. w2 = w20  -l2 ; w =(w20  -l2)½.   Y a t-il continuité de la tension uC à t=0 ? Justifier. La continuité de l'énergie stockée par le condensateur entraîne la continuité de la tension uC à t =0 : uC(t=0) = E. Y a t-il continuité de la grandeur duC/dt à t=0 ? Justifier. i = dq/dt =CduC/dt ;  La continuité de l'énergie stockée par la bobine entraîne la continuité de l'intensité : i(t=0) = 0. En déduire A et B. uC(0) = E =A ; duC/dt =-l exp(-lt) (A cos (wt) +B sin(wt)) + exp(-lt) (-Awsin(wt) + Bwcos (wt)) 0 = -l A + Bw ; B = l A /w = l /wE. uC(t) = E exp(-lt) ( cos (wt) +l/w sin(wt)). Donner l'allure de uC(t). 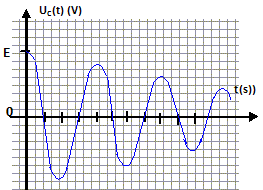On se place dans le cas où R =0. Donner l'équation différentielle satisfaite par uC(t) ainsi que sa solution. Les conditions initiales sont inchangées et l =0 : d2uC/dt2 +w20 uC(t) =0. uC(t) = E  cos (wt). Donner l'expression de la période propre T0.  T0 = 2 p / w0 = 2 p(LC)½. En présence d'humidité dans l'atmosphère, on mesure une période T0 = 27,2 µs. On donne L= 150 mH. Calculer C. T0 = 27,2 10-6 s ; L= 0,150 H ;  C = T02 /(4p2L) =(27,2 10-6)2/ (4*3,142*0,15) =1,25 10-10 F = 125 pF. On peut lire sur la notice d'un tel appareil : gamme de mesures : 10 à 90 % d'HR ; sensibilité : 0,4 pF / % d'HR ; capacité  à 43 % d'humidité : 122 pF. Sachant que C s'écrit : C = a HR + b,  déterminer les valeurs des constantes a et b. 122 =43 a + b ; dC/dHr = a = 0,4 pF/%HR ; b = 122-43 a = 122-43*0,4 =104,8 pF. C = 0,4 HR +104,8. Déterminer le taux d'humidité HR de l'atmosphère. HR =(C-104,8) / 0,4 =(125-104,8) / 0,4 = 50,5 %. Régime sinusoïdal forcé. Une autre méthode consiste à soumettre le dipole RLC à une tension sinusoïdale. 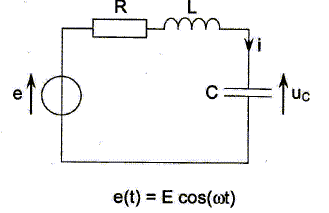On réalise le montage ci-dessous :  On associe aux tensions sinusoïdales, e(t) et uC(t) des grandeurs complexes : e =E exp(jwt) et uC(t) = UC exp(j(wt+f)) Etablir l'expression de la fonction de transfert H =uC / e. e = (R +jLw+1/(jCw) ) i ; uC = i /(jCw)) ;  H = 1 / (jRCw -LCw2 +1). On pose Q, facteur de qualité : Q = 1/R (L/C)½ ; w0 =1/(LC)½ ; Q w0 =1/(RC). H = 1 / (jw/(Qw0) -w2 / w20 +1) Déterminer le module de H. On pose x =w/w0. 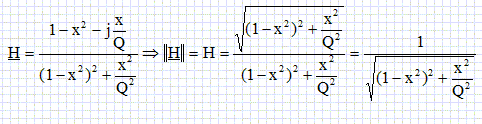H = 1/(1-x2+jx/Q) On montre que si Q >0,707, le gain passe par un maximum pour une pulsation wM qui dépend de w0 et de Q. Choisir parmi les deux expressions celle qui donne wM. 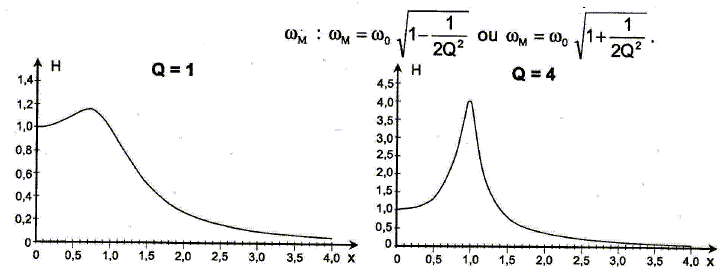Q = 4 donne x=1 soit wM =1,125 w0 ou wM =0,875 w0 soit wM ~w0. Q= 1, le graphe indique que x<1 soit  wM est bien inférieur à w0  : l'expression wM = w0  (1-1/(2Q2))½ convient. Ou bien par le calcul :  dH/dx = -½(-4x(1-x2) +2x/Q2) / ((1-x2)2 +x2/Q2)3/2 ; cette dérivée s'annule pour : -4x(1-x2) +2x/Q2=0 ; 2(1-x2) =1/Q2 1-x2 =1/(2Q2 ) ; x2 = 1-1/(2Q2 ) ; x =[ 1-1/(2Q2 )]½. x étant positif, on ne retient pas la valeur négative. Dans le cas où Q est très grand devant 1, le rapport |wM-w0| / w0 est sensiblement égal à 1/(4Q2). A.n : R = 10 W ; L = 100 mH ; C = 130 pF. Q = 1/R (L/C)½ =0,1 (0,1/1,3 10-10)½ =2773,5 ~2,8 103.  w0 =1/(LC)½ =1/(0,1*1,3 10-10)½ = 2,77 105 rad/s. 1/(4Q2) =1/(4*2773,52) =3,2 10-8. On peut dans ce cas confondre w0 et wM. Pour relier le capteur situé  àl'extérieur d'un bâtiment au dispositif de mesure situé  à l'intérieur, on utilise un câble coaxial d'une longueur d'environ 5 m de capacité Ccâble ~ 100 pF et sensible aux variations d'humidité de l'air. 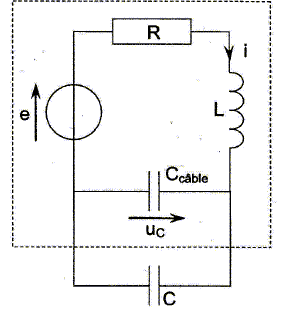le schéma équivalent est représenté : On mesure donc la capacité Céq équivalente  à C en parallèle avec Ccâble. Exprimer Céq. Les capacités s'ajoutent : Céq = C + Ccâble = C +100 pF. Or C est compris entre 105 et 140 pF ; Céq est de l'ordre de 200 pF, ce qui correspondrait  à une humidité relative supérieure à 100 %. La gamme de mesures de l'appareil est comprise entre 10 à 90 % d'HR : l'appareil serait incapable de faire une mesure.

retour -menu