L'atmosphère est constituée d'un mélange gazeux
comprenant le diazote ( 78 % en volume) et le dioxygène ( 21 % en
volume) . On y trouve aussi l'argon ( environ 1 % ) et le dioxyde de
carbone ( 0,03 %), de la vapeur d'eau et des traces d'une multitude
d'autres gaz. On donne N : 14 ; O : 16 ; Ar : 40 g/mol et R = 8,314 J
mol-1 K-1.
Etude de la
pression en fonction de l'altitude.
On néglige la vapeur d'eau et on considère l'air
sec. L'air est considéré comme un mélange idéal de gaz parfaits ; g =
9,81 N /kg dans cette partie.
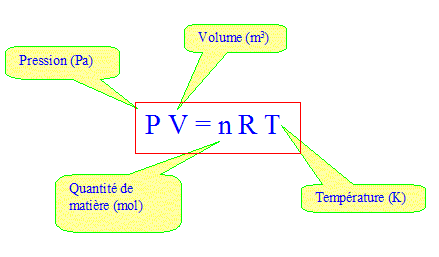
Rappeler en quelques
lignes le modèle du gaz parfait. Donner l'équation d'état.
Modèle thermodynamique : dans un gaz à basse
pression les interactions électrostatiques entre particules sont
négligeables, les molécules étant suffisamment éloignés les unes des
autres.
Dans un gaz réel, il faut prendre en compte les interactions
entre particules et tenir compte du volume des molécules constituant le
gaz.
Un gaz quelconque, sous faible pression, peut être assimilé à un gaz
parfait.
Un gaz, dans des conditions proches de la liquéfaction, ne peut pas
être assimilé à un gaz parfait.
Montrer que la masse
molaire de l'air vaut M=29 g/mol.
L'air contient : fraction molaire du dioxygène 0,21 ; fraction
molaire du diazote : 0,788 ; fraction molaire de l'argon : 0,01
M(O2) = 32 g/mol ; M(N2) = 28 g/mol.
M(air) = 0,21*32+0,78*28 + 0,01*40 =28,96 proche 29 g/mol.
Atmosphère isotherme en
équilibre.
On
appelle Oz l'axe vertical ascendant et on suppose le champ de pesanteur
uniforme.
On note respectivement P, T et µ les pression, température et masse
volumique de l'air à une altitude z quelconque et par P0, T0,
et µ0 les valeurs correspondantes à l'altitude z=0. On
prendra P0 = 1,03 bar.
On fait d'abord l'hypothèse que l'atmosphère est en équilibre isotherme
à la température T0 = 288 K.
|
Montrer que P
= µRT/M.
Loi des gaz parfaits : P V = nRT0
soit P = n/V RT0
masse volumique : µ = m/V ; n= m/M ( quantité
de matière (mol) = masse (g) / masse molaire (g/mol) )
d'où : P= m/V RT0/M ;
P= µRT0/M.
|
La loi de la
statique des fluides dans le champ de pesanteur s'écrit : dP/dz = -µg.
Montrer
qu'à l'altitude z, P(z) = P0 exp(-z/H).
En admettant que g reste constant dans l’atmosphère :
dP/dz= -µg et µ=PM/(RT0).
d'où : dP/dz = -PMg/(RT0) ; dP/ P = -Mg/(RT0) dz
; d ln (P) = -Mg/(RT0) dz
ln P = -Mg/(RT0) z + Cte.
si z=0; P= P0 d'où : ln (P/P0) = -Mg/(RT0)
z.
P = P0
exp(-Mg/(RT0) z).
H = RT0/
(Mg) = 8,314*288 /(0,029*9,81) =8,4 103 m= 8,4 km.
exp(-z/H)
étant sans dimension, H et z s'expriment dans la même unité, le mètre.
H peut être considérée comme " une constante caractéristique " de ce
modèle, comparable à la "constante de temps" d'un dipôle RC.
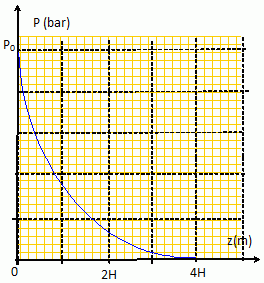
Tracer
l'allure de la courbe P(z) et calculer P (z= 5,0 km).
P(z=5) = 1,03 exp(-5 /8,4) = 1,03*0,55 = 0,568 ~0,57 bar.
Déterminer
l'expression de µ(z) en fonction de µ0, z et H. Calculer µ0
et µ(z=5,0 km).
P= µRT0/M ; H = RT0/
(Mg) ; P = µgH ; µ =P/(gH)
µ =P0/(gH)exp(-z/H) ; à l'altitude z=0 : µ0 =P0/(gH) = 1,03 105
/(9,81*8,4 103) =1,25 kg m-3.
µ =µ0
exp(-z/H).
µ(z= 5 km) = 1,25 exp(-5/8,4) = 0,69 kg m-3.
Equilibre
polytropique de l'atmosphère.
Le modèle de l'atmosphère en équilibre isotherme n'étant pas réaliste,
on suppose désormais que dans la troposhpère ( jusqu'à une altitude de
10 km), la température de l'air varie avec l'altitude sous la forme :
T(z) = T0(1-kz) où k est une constante positive.
Montrer
que la pression à l'altitude z varie sous la forme P(z) = P0(1-kz)a.
dP/dz= -µg et µ=PM/(RT).
d'où : dP/dz = -PMg/(RT) ; dP/ P = -Mg/(RT0(1-kz)) dz
; d ln (P) = -Mg/(RT0) (1-kz)-1dz ;
On pose u = 1-kz ; du = -kdz d'où : (1-kz)-1dz =-1/k du/u = -1/k ln u.
ln P = +Mg/(kRT0) ln (1-kz) + cste ;
à z=0 : ln P0 = cste d'où : ln P = +Mg/(kRT0) ln (1-kz) +ln P0 ; on pose a = Mg/(kRT0).
ln( P/ P0) = ln (1-kz)a ; P(z) = P0(1-kz)a.
Donner l'expression de µ(z) en fonction de µ0, z, k et a.
P
= µRT/M = µRT0(1-kz)/ M ; µ =PM / (RT0(1-kz))
µ =P0(1-kz)aM / (RT0(1-kz)) ; µ=P0(1-kz)a-1M / (RT0)
à l'altitude z=0 : µ0 =P0M / (RT0) ; µ =µ0(1-kz)a-1.
AN : k = 2,20 10-5 m-1 ; T0 = 288 K.
Calculer P et µ pour z = 5,0 km.
a = Mg/(kRT0) = 0,029 *9,81 /(2,20 10-5*8,314*288) =5,4.
P(z= 5,0 km) = 1,03(1-2,20 10-5*5000)5,4=0,55 bar.
µ(z-5 km) = 1,25(1-2,20 10-5*5000)4,4=0,75 kg m-3.
|
Ascension d'un ballon à hélium.
On se place dans le cas de l'équilibre polytropique de l'atmosphère.
Un ballon de volume maximal Vmax = 1000 m3 est partiellement gonflé au sol avec un volume V0 = 500 m3
d'hélium. La masse totale de l'enveloppe ( hélium non compris) et de la
nacelle est m = 450 kg. L'enveloppe est munie d'une soupape qui assure
l'équilibre thermique et mécanique entre l'hélium et l'air extérieur.
Montrer
que le rapport des mase volumique de l'hélium contenu dans l'enveloppe
et de l'air extérieur est indépendant de l'altitude.
d = µHe / µair ; du fait de l'équilibre thermique :
µHe =µ0(1-kz)a-1 ; µair =µ0(1-kz)a-1 ; d = µHe 0 / µair 0 ;
Calcul de d si M(He) = 4,0 g/mol.
µair 0 =P0Mair / (RT0) ; µHe 0 =P0MHe / (RT0) ; d = MHe /Mair = 4/29 =0,138 ~0,14.
On appelle force ascensionnelle la somme des forces extérieures s'exerçant sur le ballon, en mouvement rectiligne suivant Oz.
Déterminer l'expression de cette force au sol, en fonction de g, m, d, µ0 et V0.
Masse d'air contenue dans la montgolfière : V0 µHe =V0 d µair = V0 d µ0 ;
poids de l'enveloppe + nacelle + hélium : P=
(m+V0 d µ0)g, verticale vers le bas.
Poussée d'Archimède = poids du volume d'air
déplacé = V0 g µ0, verticale vers le
haut
La force ascensionnelle F est égale à la
différence entre la poussée et le poids :
F=V0 g µ0 -(m+V0 d µ0)g = V0 g µ0 (1-d)-mg.
Quand la montgolfière va commencer à
décoller, F est positive :
V0 g µ0 (1-d) > mg ; V0 µ0 (1-d) > m ;
500 *1,25 (1-0,14) = 537,5 kg, valeur supérieure à 450 kg : le ballon décolle.
Exprimer le volume V(z) au cours de l'ascension tant que V(z) < Vmax.
La quantité de matière d'hélium reste constante.
P(z) = P0(1-kz)a ;
T(z) = T0(1-kz)
V(z) = nHeRT(z) / P(z) = nHeRT0(1-kz) / (P0(1-kz)a )
V(z) = nHeRT0 / P0 (1-kz)1-a ; avec nHe = P0V0/(RT0)
V(z) = V0 (1-kz)1-a .
Vmax = V0 (1-kz1)1-a ; 1000 = 500(1-2,2 10-5z1)-4,4 ; 1/4,4 =0,227
2-0,227 =0,854 = 1-2,2 10-5z1 ; z1 =6617 m ~6,6 km.
Lorsque le ballon atteint cette altitude, le volume de l'enveloppe
reste constant. Le ballon continue à s'élever, le gaz s'échappe alors
de la soupape pour assurer l'équilibre thermique et mécanique avec
l'air extérieur.
Montrer que la force ascensionnelle décroît jusqu'à s'annuler.
Le ballon atteint alors son plafond d'altitude z2.
La quantité de matière d'hélium contenue dans le ballon vaut : n=P(z) V / ( RT(z) ) ;
masse d'hélium : n M(He)= M(He) P(z) V / (RT(z)) = M(He) V / R P0(1-kz)a /T0(1-kz)
masse d'hélium : M(He) V P0/ (RT0 )(1-kz)a-1 =M(He) V n0 /V0(1-kz)a-1 ;
Le poids de l'ensemble vaut : P=
(m+M(He) V n0 /V0(1-kz)a-1) g ;
La poussée change et vaut : V g µ(z) =V g µ0(1-kz)a-1 ;
La force ascensionnelle F vaut : V g µ0(1-kz)a-1-(m+M(He) V n0 /V0(1-kz)a-1) g ;
F =V g µ0(1-kz)a-1- M(He) V n0 /V0(1-kz)a-1g - mg
F = g { V(1-kz)a-1 [µ0- M(He)n0 /V0] -m }
Le terme V[µ0- M(He) n0 /V0] est constant ; 1-kz est inférieur à 1 et diminue si z augmente ; a-1 est positif ;
(1-kz)a-1 va donc diminuer si z augmente.
0 = V(1-kz2)a-1 [µ0- M(He) n0 /V0] - m
n0 = 1,03 105*500 / (8,314*288) =2,15 104 mol.
450 = 1000( 1-2,2 10-5 z2)4,4 [1,25-0,004 *2,15 104 / 500]
0,45 =( 1-2,2 10-5 z2)4,4 *1,078 ; 1/4,4 =0,227 ;
(0,45/1,078)0,227 = 1-2,2 10-5 z2 ; 0,82 = 1-2,2 10-5 z2 ; z2 =8176 m = 8,2 km.
|
|

