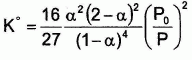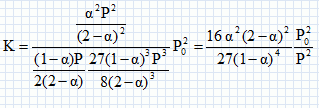Décomposition N2O, synthèse de NH3, concours capes interne 2010.

Décomposition de N2O. A température sufissament élevée, le monoxyde de diazote se décompose en diazote et dioxygène selon une réaction pratiquement totale : 2N2O(g) =2 N2(g) + O2(g). On introduit dans un réacteur thermostaté à la température T, de volume constant V, préalablement vidé, une quantité n1 de monoxyde de diazote à la pression initiale P1. On suit l'évolution de la réaction en mesurant la pression totale P en fonction du temps. A T=600°C on obtient les résultats suivants : t en minute 0 25 45 90 P / P1 1,000 1,120 1,195 1,314 On suppose que la réaction est d'ordre 1 par rapport à N2O et on appelle k la constante de vitesse  à la température T. Soit x l'avancement de la réaction à l'instant t. Montrer que x = ½n1(1-exp(-2kt)). avancement (mol) 2N2O(g) =2 N2(g) + O2(g) initial 0 n1 0 0 en cours x n1-2x 2x x La vitesse de la réaction s'écrit : v =1/V dx/dt = k [N2O] ;  vitesse de disparition de N2O : vd= -d[N2O] /dt = -1/Vdn(N2O)/dt = -1/V d(n1-2x) /dt = 2 dx/dt =2v ; dx/dt  = k( n1-2x) ; dx/( n1-2x) = kdt On pose u = n1-2x , du = -2dx ; -½du/ u = kdt ; d(lnu) = -2kdt ; ln u = -2kt + cste. A t = 0, u = n1 d'où : ln( (n1-2x)/n1 )= -2 kt  ; n1-2x = n1exp(-2kt) x = ½n1(1-exp(-2kt)). Déterminer l'expression du nombre total de moles gazeuses nTG en fonction de n1, k et t. La dernière du tableau d'avancement donne : nTG = n1+ x = n1+½n1(1-exp(-2kt)) = ½ n1 ( 3-exp(-2kt)) En déduire que P/P1 = ½(3-exp(-2kt)). P = nTG RT/V ; P1 = n1 RT/V ; P/P1 = nTG / n1 = ½(3-exp(-2kt)). On veut tracer une courbe permettant de vérifier l'ordre 1 et calculer k. Si on impose le temps en abscisse, que peut-on mettre en ordonnée ?  2P/P1 =3-exp(-2kt) ; exp(-2kt) = 3-2P/P1  ;  ln(3-2P/P1) = -2kt ; On porte en ordonnée  ln(3-2P/P1) et le temps en abscisse : on obtient une droite de pente -2k Vérifier ces résultats expérimentaux et en déduire la valeur de k. t(min) 0 25 45 90 ln(3-2P/P1) 0 -0,274 -0,494 -0,989 k = ln(3-2P/P1) / (-2t) xxx 5,48 10-3 5,49 10-3 5,49 10-3 ln(3-2P/P1) est proportionnel au temps. Les résultats expérimentaux vérifient l'hypothèse d'un ordre 1 pour N2O. La constante de vitesse vaut k = 5,5 10-3 min-1.   En déduire le temps de demi-réaction t½. A t= t½, l'avancement est égal à la moitié de l'avancement final. La réaction étant totale, l'avancement final est égal à ½n1. à t½, l'avancement vaut 0,25 n1 = ½n1(1-exp(-2kt½)). 0,5 = 1 - exp(-2kt½) ; 0,5 = exp(-2kt½) ; ln 0,5 = -2kt½ ; t½ = ln 2 / (2k) = 0,693 / (2*5,48 10-3) = 63 s. Synthèse de NH3. On étudie la réaction en phase gazeuse N2(g) + 3H2(g) = 2 NH3(g). On assimile les gaz à des gaz parfaits et le mélange de gaz est supposé idéal. On donne à 298 K : R = 8,314 J K-1 mol-1. DfH ( kJ mol-1) S° ( J K-1 mol-1) N2(g) 0 191,5 H2(g) 0 130,6 NH3(g) -46,2 192,5 Industriellement comment prépare t-on le dihydrogène et le diazote ?  Le diazote est préparé par distillation de l'air liquide ou par passage de l'air comprimé à travers des membranes semi-perméables. Le dihydrogène est préparé par : - Reformage du gaz naturel ( CH4 + H2O) vers 900 °C sous 10 bars, en présence de catalyseur au nickel. - Electrolyse d'une solution aqueuse alcaline ( obtention de H2 de grande pureté). - Craquage du méthanol. Justifier pourquoi l'enthalpie standard de formation de N2(g) et celle de H2(g) sonr nulles à 298 K. L'état standard de référence d'un corps simple à la température T est l'état physique le plus stable  à la température T L'enthalpie standard de formation d'un corps composé est l'enthalpie standard de la réaction de formation de ce corps à partir des éléments pris dans leur état standard. Dans le cas du dihydrogène ( ou du diazote ) il s'agit de la réaction de formation de N2(g) à partir de N2(g) ( formation du corps à partir de lui même ). L'enthalpie standard de formation de N2(g) est donc nulle. On pourrait dire la même chose à 350 K Calculer  à 298 K, l'enthalpie standard de cette réaction DrH° ; commenter son signe. DrH°  = 2DfH(NH3) - 3DfH(H2)-DfH(N2) = 2*(-46,2) = -92,4 kJ / mol. Cette valeur étant négative, la réaction est exothermique. Calculer  à 298 K, l'entropie standard de cette réaction DrS° ; pouvais t-on prévoir son signe ? DrS°  = 2S°(NH3) - 3S°(H2)-S°(N2) = 2*192,5 -3*130,6-191,5= -198,3 J K-1 mol-1. Initialement on  a 4 molécules ; à la fin , il n'y a plus que 2 molécules : l'ordre augmente, la variation d'entropie est négative. Quelle est l'influence d'une élévation de pression à température constante sur cet équilibre ? Justifier. L'équilibre est déplacé dans le sens d'une diminution du nombre de molécules ( ce qui correspond à une diminution de la pression), cest à dire dans le sens direct. On suppose par la suite que DrH° et DrS° sont indépendants de la température.  Comment appelle t-on cette approximation ? approximation d'Ellingham. Quelle est l'influence d'une élévation de température à pression constante sur cet équilibre ? Justifier. La réaction dans le sens direct étant exothermique, une élévation de température déplace l'équilibre dans le sens indirect ( vers la gauche) ; la réaction endothermique est favorisée par une élévation de température ( loi expérimentale de Van't Hoff ). Constante d'équilibre. Donner dans le cadre de cette approximation, l'expression de l'enthalpie libre standard DrG°en fonction de la température. DrG° = DrH° -TDrS° ; DrG° = -92,4 103 +198,3 T ( en J mol-1) Déterminer la valeur de la constante d'équilibre K à 0°C et à 450 °C. DrG° =-RT ln K ; DrG° (273 K)= -92,4 103 +198,3 *273 =-3,826 104 J mol-1. ln K0 = 3,826 104 (8,314 *273 )=16,86 ; K0 = 2,1 107. DrG° (723 K)= -92,4 103 +198,3 *723 =5,097 104 J mol-1. ln K723 = -5,097 104 (8,314 *723 )= -8,48 ; K723 = 2,1 10-4. Cette synthèse est réalisée  à 450°C. Justifier ce choix. A la température de la pièce, la réaction est lente ; élever sa température augmente la vitesse de réaction, mais  favorise la réaction inverse (endothermique). Selon le principe de Le Chatelier, une augmentation de la pression favorisera la réaction qui diminue la pression du système à l'équilibre. Une pression d'environ 200 bar modifie suffisamment la constante d'équilibre pour obtenir une production raisonnable. Le catalyseur exige une température d'au moins 400 °C pour être efficace. On réalise la réaction à une pression totale P et à une température T maintenue à 450 °C, température pour laquelle la constante d'équilibre vaut K =2,1 10-4. On rappelle que l'activité ai d'une espèce gazeuse Ai dans un mélange idéal de gaz parfaits s'écrit ai = Pi / P0 où Pi est la pression partielle de cette espèce. Comment appelle t-on la pression P0 et quelle est sa valeur ? P0 est une pression de référence que l'on choisit égale à 1 bar. Exprimer la constante d'équilibre K de la synthèse de NH3 en fonction  des pressions partielles des différentes espèces et de P0. K = a2NH3 / (aN2 a3H2) = P2NH3 P20/ (PN2 P3H2). On suppose que l'on part d'un mélange stechiométriques de N2 et de H2 ( on note n0 la quantité de matière initiale de N2) et on appelle a le coeficient de dissociation de N2 à l'équilibre. Etablir le tableau d'avancement de la réaction et en déduire le nombre total de moles gazeuses à l'équilibre en fonction de n0 et a. avancement volumique (mol/L) N2(g) +3H2(g) + 2NH3(g) initial 0 n0 3n0 0 en cours x n0-x 3n0-3x 2x équilibre xéq n0-xéq 3n0-3xéq 2xéq Nombre total de moles à l'équilibre : N = 4n0-2xéq. a =xéq / n0 ; N =4n0-2an0 = 2n0 (2-a). En déduire l'expression des pressions partielles à l'équilibre en fonction de P, P0 et a. PNH3 = 2xéq / N P = 2an0 /(2n0 (2-a)) P = a / (2-a) P ; PN2 = (n0-xéq)/N P = (n0-an0) /(2n0 (2-a)) P =(1-a) / (2(2-a)) P ; PH2=3n0-3xéq / N P = 3( n0-an0 )/(2n0 (2-a)) P =3(1-a) / (2(2-a)) P. 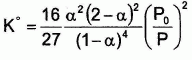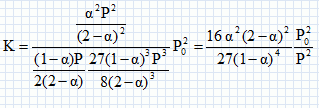Montrer que  : Le taux de dissociation à l'équilibre vaut a = 0,52 pour une température de 450°C. Calculer la pression P. 2,1 10-4 *27(1-0,52)4 P2 = 16*0,522(2-0,52)2 ; 3,01 10-4P2 = 9,477 ; P2 =3,148 104 ; P= 177 ~1,8 102 bar.

retour -menu