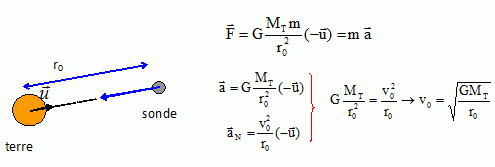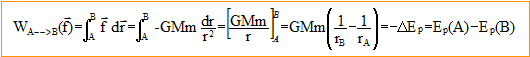Mécanique : envoi d'une sonde sur Mars, éllipse de transfert de Hohmann, capesa 2010.

Le but est d'utiliser la trajectoire la plus économique. La sonde sera assimilée à un point matériel. On considère que la planète Mars et la Terre décrivent autour du Soleil des trajectoires circulaires respectivement de rayon rM = 23 107 km à la vitesse vM =24 km/s et de rayon rT = 15 107 km à la vitesse vT=30 km/s. Dès que la sonde quitte la zone d'influence d'une planète, on considère qu'elle subit uniquement l'attraction gravitationnelle du soleil. MM = 6,4 1023 kg ; MT = 6,0 1024 kg ; MS = 1,9 1030 kg ; RM =3,4 103 km ; RT =6,4 103 km ; masse de  la sonde m = 30 106 kg ; G = 6,7 10-11 SI. Mouvement de la sonde autour de la terre. On se place dans le référentiel géocentrique supposé galiléen ; on ne tient compte que de l'attraction terrestre. On place la sonde en orbite d'attente circulaire basse au voisinage de la terre. La sonde décrit alors une trajectoire circulaire de rayon r0 à la vitesse v0 de centre le centre de la terre. Sur cette trajectoire la sonde se trouve à une altitude z0 = 200 km au dessus du sol terrestre. Exprimer la vitesse v0 en fonction de G MT er r0 puis la calculer. 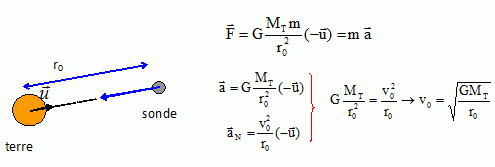r0 = RT + z0 = 6,4 106 +2 105 =6,6 106 m ; v0=(6,7 10-11* 6,0 1024 /6,6 106 )½=7,8 103 m/s. En déduire l'expression de l'énergie cinétique de la sonde Ec0 en fonction de G, MT, m et r0. Ec0 = ½mv02 =½mGMT/r0. Etablir l'expression de l'énergie potentielle de gravitation Ep0. ( L'énergie potentielle est nulle lorsque la sonde est très loin de la terre) Les vecteurs sont écrits en gras et en bleu. Le satellite n'est soumis qu'à la force de gravitation attractive exercée par la Terre. La direction de cette force passe toujours par le point O, centre de la Terre : il s'agit donc d'un champ de forces centrales. f(r) = GMm/r2(-u) Montrons que la force f qui s'exerce sur le satellite S dérive d'une énergie potentielle de gravitation Ep. Le travail de la force f(r) ne dépend que des positions initiale et finale ( peu importe le chemin suivi) : la force est conservative. On peut associer à cette force, une fonction scalaire ou énergie potentielle notée Ep(r), définie à une constante près ; la variation de l'énergie potentielle entre les points A et B est égale à l'opposée du travail de la forcef(r) entre ces points. 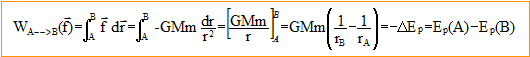En prenant B situé à l'infini ( par convention cette énergie potentielle est nulle à l'infini), il vient : Ep0 = -GMTm/r0. En déduire une relation entre Ec0 et Ep0. Ec0 =-½Ep0. Exprimer l'énergie mécanique totale Em0 et faire l'application numérique.   Em0 = Ec0 +Ep0. Em0 =-½Ep0+Ep0 = ½Ep0 = -½GMTm/r0. L'énergie mécanique augmente lorsque r0 croït et s'annule lorsque le sonde est très loin de la terre. Em0 = -0,5*6,7 10-11* 6,0 1024 *30 106 /6,6 106 = -9,1 1014 J.   Sortie de l'attraction terrestre. A partir de cette orbite d'attente, on désire envoyer la sonde sur Mars. Exprimer le travail minimal à fournir à la sonde en orbite autour de la terre pour qu'elle puisse s'échapper de l'attraction terrestre. L'énergie mécanique est positive ou nulle, ce qui caractérise un corps pouvant s'échapper de l'attraction terrestre. Em infini = 0 ; Ep infini = 0 ;  Em0 =½Ep0 ; variation de l'énergie potentielle :  -½Ep0 ; La variation de l'énergie potentielle est égale à l'opposé du travail à fournir : W = ½Ep0 =½GMTm/r0. Exprimer la nouvelle vitesse v'0 de la sonde juste après avoir reçu ce travail et avant d'avoir quitté l'orbite basse. faire l'application numérique. ½mv'02 - ½mv20 = W = ½GMTm/r0. v'02 - v20  =GMT/r0 ; v'02 = v20 +GMT/r0 ; v'0 =((7,8 103)2 +6,7 10-11* 6,0 1024  /6,6 106 )½ = 11 103 m/s. Décrire la trajectoire de la sonde après qu'elle ait quitté l'orbite circulaire. pour v'0=Vlibération le satellite s'éloigne indéfiniment de la terre en décrivant un arc de parabole. Décrire la trajectoire qu'aurait la sonde si le travail fourni était supérieur au travail minimal. L'énergie mécanique de S est strictement positive, la trajectoire est une hyperbole. On communique à la sonde une vitesse  v1 par rapport à la terre supérieure ou égale à la vitesse v'0. La sonde échappe à l'attraction terrestre et possède une vitesse v2 par rapport à la terre. Exprimer v1 en fonction  de v2, G, MT et r0. Energie mécanique de la sonde à l'infini : Ep infini = 0 ; Ec infini = ½mv22 ; Em = ½mv22 ; Energie mécanique de la sonde  à l'altitude z0, juste après avoir reçu le travail : Ep0 + ½mv21 = -GMTm/r0+ ½mv21 ; conservation de l'énergie mécanique : -GMTm/r0+ ½mv21 = ½mv22 ; -2GMT/r0+ v21 = v22 ; v21 = v22 +2GMT/r0 ; v1 =( v22 +2GMT/r0 )½. Ellipse de transfert de Hohmann. La sonde échappe à l'attraction terrestre et devient un satellite du soleil. Une fois éloignée de la terre, elle possède une vitesse v2 dans le référentiel géocentrique et v3 dans le référentiel héliocentrique. On souhaite que sa trajectoire autour du soleil rencontre celle de Mars. Pour cela la sonde doit décrire une éllipse dont le soleil est un foyer ; cette éllipse est coplanaire aux trajectoires circulaires de la terre et de Mars autour du soleil. Elle est tangente à son périhélie à la trajectoire de la Terre autour du soleil et à son aphélie à la trajectoire de Mars autour du soleil. On indique que le sens de révolution de la sonde autour du soleil est identique à celui de la Terre et de Mars autour du soleil. On se place dans le référentiel héliocentrique supposé galiléen et on ne tient  compte que de l'attraction gravitationnelle du soleil. Calculer le demi-grand axe, noté a de la trajectoire élliptique de la sonde. On pourra négliger r0 devant rT. a = ½(r1 + r2 )= ½(rM + rT) =0,5 (23 107 + 15 107 )=19 107 km =1,9 1010 m . Etude des propriétés de la trajectoire. La seule force qui s'exerce sur la sonde est une force dite centrale, justifier l'appellation. Cette force est constamment dirigée vers le centre du soleil, point fixe dans le référentiel héliocentrique. Enoncer la loi des aires. 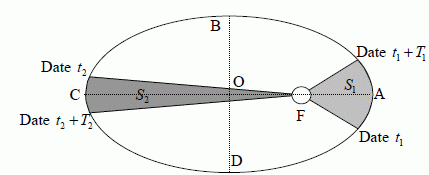Loi des aires : le satellite passe de P à P1 et de A à A1 pendant la même durée : aire S1= aire S2. Evaluer le temps de vol entre la terre et mars. On pourra utiliser la troisième loi de Kepler. La sonde parcourt la moitié de l'ellipse entre A et P. La durée du parcours est la moitié de la période de révolution T sur l'ellipse. La troisiéme loi de Kepler donne la période T en fonction de a. T² = 4p² / (GMS) a3. T = 2*3,14/(6,7 10-11*1,9 1030) ½ *(3,8 1010)1,5 =4,12 106 s  ; ½T = 2,1 106 s ~24 jours. Sur la trajectoire elliptique, l'énergie mécanique de la sonde se conserve et vaut : Em = -GmMS/(2a). Pour se placer sur cette trajectoire elliptique, la sonde doit  avoir une vitesse v3 dans le référentiel héliocentrique après sa sortie de l'attraction terrestre au périhélie de l'ellipse de transfert. Exprimer cette vitesse en fonction de rT, rM, G et MS. Faire l'application numérique. Energie potentielle de la sonde  : -GMS m / rT ; énergie cinétique ½mv23. Em = -GmMS/(2a) = -GMS m / rT + ½mv23. -GMS/a +2GMS  / rT = v23. v3 = [GMS  ( 2/rT -1/(rT+rM)) ]½. v3 = [6,7 10-11*1,9 1030  ( 2/1,5 1011 -1/(1,5 1011+2,3 1011)) ]½~3,7 104 m/s = 37 km/s. En déduire la vitesse v2 correspondante de la sonde par rapport au référentiel géocentrique à cet instant. La sonde et la terre tournent dans le même sens : Vsonde/ soleil = Vsonde/ terre +Vterre/ soleil ; v3 = v2 + vT ; v2 = 37-30 = 7 km/s. Evaluer la valeur de la vitesse v4 de la sonde par rapport au soleil lors de son arrivée à l'aphélie. Energie potentielle de la sonde  : -GMS m / rM ; énergie cinétique ½mv24. Em = -GmMS/(2a) = -GMS m / rM + ½mv24. -GMS/a +2GMS  / rM = v24. v4 = [GMS  ( 2/rM -1/(rT+rM)) ]½. v4 = [6,7 10-11*1,9 1030  ( 2/2,3 1011 -1/(1,5 1011+2,3 1011)) ]½~2,78 104 m/s = 28 km/s. Trajectoire autour de Mars.   On se place dans le référentiel Rmars supposé galiléen, centré sur Mars et en translation par rapport à RS. On ne tient compte que de la gravitation marsienne. Calculer la vitesse v5 de la sonde par rapport à la planète mars à son arrivée au voisinage de Mars. La sonde et Mars tournent dans le même sens : Vsonde/ soleil = Vsonde/ mars +Vmars/ soleil ; v4 = v5 + vM ; v5 = 27,8-24 = 3,8 km/s. Lorsque la sonde entre dans le champ de gravitation de Mars on peut considérer que la sonde, par rapport à Mars, vient de l'infini. En déduire sa trajectoire par rapport à Mars. Energie potentielle de la sonde  : -GMM m / rM ; énergie cinétique ½mv25. Em =m( -GMM  / rM + ½v25 )   Em =3 107 ( -6,7 10-11 *6,4 1023 / 3,4 106 + ½(3,8 103)2 ) = -1,6 1014 J. L'énergie mécanique étant négative, la trajectoire est une ellipse. L'objectif est de mettre la sonde sur une orbite circulaire de rayon r6 autour de Mars à une altitude zM= 100 km ; il faut donc réaliser un freinage de la sonde. Exprimer la vitesse v6  que doit posséder la sonde par rapport à Mars sur cette orbite circulaire en fonction de G, MM et r6. calculer v6. r6 = RM + zM = 3,4 106 + 105 = 3,5 106 m. v6 = (GMM / r6)½ =( 6,7 10-11 *6,4 1023 / 3,5 106)½ =3,5 103 m/s = 3,5 km/s. Evaluer le travail effectué par les rétrofusées pour réaliser ce changement d'orbite. Energie mécanique finale : m( -GMM  / r6 + ½v26 ) 3 107 ( -6,7 10-11 *6,4 1023 / 3,5 106 + ½(3,5 103)2 ) = -1,84 1014 J. La diminution de l'énergie mécanique est égal au travail des rétrofusées : -1,84 1014  - ( -1,6 1014 ) = -2,4 1013 J.

retour -menu