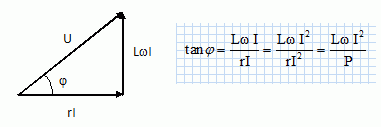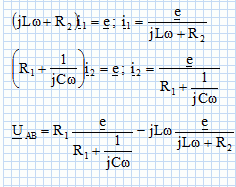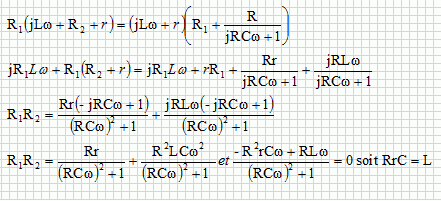Moteur électrique, dipôle RL, régime sinusoïdal forcé, pont de Wheatstone capesa 2010.

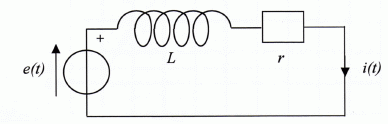
Etude des bobines. Une bobine du moteur est modèlisée par une bobine idéale d'inductance L en série avec un conducteur ohmique de résistance r. Réponse à un échelon de tension. On alimente la bobine par un générateur idéal de tension e(t) délivrant un échelon de tension. A t=0, e(t) passe brutalement de 0 à E volt. Etablir l'équation différentielle qui régit l'évolution de l'intensité i(t) en fonction de E, r, L et t. additivité des tensions : E = r i + Ldi/dt di/dt +r/L i = E/r et en posant t = L/r : di/dt + i/t = E / L. Etablir l'expression du portrait de phase di/dt = f(i).( Préciser les points particuliers permettant d'évaluer r et L, connaissant E) di/dt = E / L -  i/t . A t =0, la continuité de l'intensité conduit à : i(0)=0 ; [di/dt]t=0 = E / L. A t suffisamment grand ( t < 5t), l'intensité est constante et vaut I : [di/dt]t infini =0 et I = E / r. Tracer l'allure du portrait de phase. 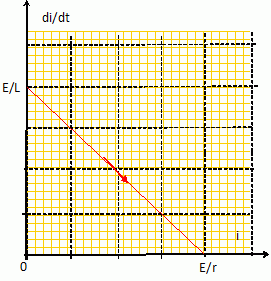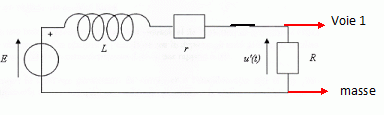On considère à présent le circuit ci-dessous, R étant la résistance d'un conducteur ohmique et E la force électromotrice d'un générateur idéal de tension continue. Le circuit étant ouvert, on ferme l'interrupteur à l'instant t=0. Indiquer le mode opératoire permettant de visualiser la réponse u'(t) sur un oscilloscope. On pose t = L/(R+r). Etablir la loi horaire de la tension u'(t) en fonction de E, R, r, t et t ? Additivité des tensions : E =Ldi/dt + (r+R) i avec i = u'(t) / R E = L / Rd u'(t) / dt +(r+R)/R u'(t) E R/ L = du'(t) / dt +  (r+R)/L u'(t) ; E R/ L = du'(t) / dt + 1/t u'(t). (1) Solution particulière de (1), régime permanent : I = E /(R+r)  ; u'(t) = RI = RE/(R+r) Solution générale de l'équation différentielle sans second membre : u'(t) = A exp (-t/t) avec A une constante. Solution générale de (1) : u'(t) = A exp (-t/t) +RE/(R+r). A t=0, u'(0) = 0 : A = -RE/(R+r) u'(t) = RE/(R+r) (1-exp (-t/t)). Indiquer la dimension et le sens physique de la grandeur t. Il s'agit de la constante de temps, exprimée en seconde : au bout d'une durée voisine de 5 t, le régime permanent est atteint. On définit le temps de montée tm comme le temps que met la tension u'(t) pour passer de 10 %  à 90 % de sa valeur en régime permanent. Montrer que tm = t ln9. u'(t10) =0,1 RE/(R+r)= RE/(R+r) (1-exp (-t10/t)) ; 0,1 = 1-exp (-t10/t) ; exp (-t10/t) = 0,9 ; -t10/t = ln  0,9 ; t10= -t  ln  0,9 u'(t90) =0,9 RE/(R+r)= RE/(R+r) (1-exp (-t90/t)) ; 0,9 = 1-exp (-t90/t) ; exp (-t90/t) = 0,1 ; -t90/t = ln  0,1 ; t90= -t  ln  0,1 tm = t90- t10= t  ln  0,9 -t  ln  0,1 = t  (ln  0,9 - ln  0,1) = t  (ln (0,9/0,1)) = t  ln 9. 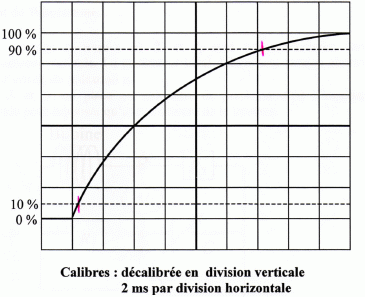On relève la courbe u'(t) suivante : Déduire la valeur de t par la méthode du temps de montée. tm ~ 6 divisions ~ 12 ms = 0,012 s. t = tm/ln9 =0,012 / ln9 = 5,46 10-3 ~ 5,5 10-3 s. La mesure de la tension maximale atteinte par u'(t) donne 6,94 V. En déduire la valeur de la résistance r et de l'inductance L de la bobine ( E = 10,0 V et R = 100 ohms). u'(t) max = RE/(R+r) = 6,94 V ; 1000 / (100+r) = 6,94 ; 1000 = 694 +6,94 r ; r =44,1 W. t = L/(R+r) = 5,46 10-3 ; L = 5,46 10-3 *144,1 = 0,787 H. Une fois le régime permanent atteint, un opérateur décide d'ouvrir l'interrupteur. Il s'agit d'un interrupteur mécanique et on observe une petite étincelle à l'ouverture. Proposer une explication à ce phénomène. A l'ouverture de l'interrupteur la bobine restitue brutalement l'énergie préalablement stockée ( d'où l'étincelle ). L'étincelle correspond à la conduction de l'air entre les deux bornes très proches de l'interrupteur que l'on ouvre. Réponse en régime sinusoïdal forcé. On alimente une bobine réelle par un courant sinusoïdal de pulsation w d'intensité efficace I sous la tension efficace U. On observe à l'oscilloscope le déphasage noté j de u(t), tension aux bornes de la bobine réelle ( de caractéristiques L et r), par rapport à i(t). Représenter le montage permettant de visualiser à l'oscilloscope u(t) et i(t). Indiquer la méthode permettant la mesure du déphasage j sur l'écran de l'oscilloscope. La tension  aux bornes d'un conducteur ohmique de résistance R, et l'intensité qui le traverse sont proportionnelles : visualiser cette tension, c'est visualiser l'intensité au facteur R près. 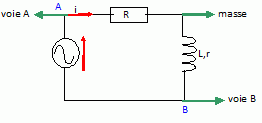A partir des deux courbes : une période T correspond à 2p radians ; un décalage Dt entre deux signaux correspond à :  j = 2p Dt / T ou -2p Dt / T. On peut aussi utiliser la méthode de Lissajous. Exprimer la puissance moyenne P reçue par la bobine réelle en fonction de U, I et j en partant de l'expression de la puissance instantanée p(t). tension aux bornes de la bobine u(t) =2½U sin (wt+j) ; l'intensité i est du type i(t) = 2½I sin ( wt) puissance instantanée : p(t) = u i =2U I sin (wt+j) sin ( wt) sin (wt+j) sin ( wt) = ½[cos j -cos(2wt+j)] p(t) = U I[cos j -cos(2wt+j)] Pour obtenir la puissance moyenne, il faut intégrer entre 0 et T et diviser le résultat par T ; la valeur moyenne d'une fonction sinus ou cosinus est nulle sur une période. par suite la puissance moyenne vaut P = UIcos j. Etablir l'expression P = rI2 avec r, résistance interne de la bobine. tension aux bornes de la bobine u(t) = Ldi/dt + r i ; puissance instantanée : p(t) = u i = L i di/dt + r i2 = ½Ld(i2) / dt + r i2. L'intensité i est du type i(t) = 2½I sin ( wt) ; i2 =2I2 sin2(wt) = I2(1-cos(2wt)) ; d(i2) / dt = 4I2sin ( wt) cos ( wt) = 2I2sin ( 2wt) p(t) = LI2sin ( 2wt) + r I2(1-cos(2wt)) Pour obtenir la puissance moyenne, il faut intégrer entre 0 et T ; la valeur moyenne d'une fonction sinus ou cosinus est nulle sur une période. par suite la puissance moyenne vaut P = r I2. Etablir l'expression L = Ptanj / (wI2). 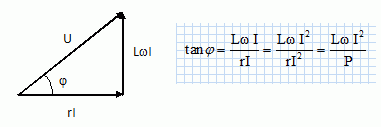AN : P = 1,00 MW ; I = 150A ; j = 80,0° ; f = 50 Hz. r = P / I2 = 1,00 106 / 1502 = 44,4 W. L = 1,00 106 tan 80,0 / (2*3,14*50*1502 )=0,803 H. Etude par pont de Wheatstone.   On considère le montage ci-dessous où R1 et R2 sont des conducteurs ohmiques et C un condensateur de capacité  variable. le générateur idéal délivre une tension sinusoïdale qui a pour expression : e(t) = E cos(wt). Entre les points A et B on place un voltmètre de précision dont l'impédance d'entrée est suffisamment grande pour supposer qu'aucun courant ne le traverse. 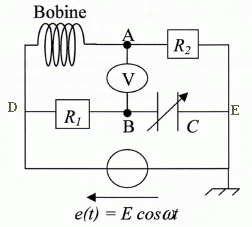Dans un premier temps on néglige la résistance interne de la bobine. Exprimer l'amplitude complexe de la différence de potentiel complexe VA-VB en fonction de E, R1, R2, C, L et jw. UDA = Z1 i1 = jLw i1  ; UDB = Z2 i2 =R1  i2 ; UAE = Z3 i3 =R2  i3 ; UBE = Z4 i4  = 1/ (jCw) i4. UAB =-UDA +UDB =UAE - UBE ; UAB =-jLw i1  +R1  i2  = R2  i3 -1/ (jCw) i4. Aucun courant ne traverse le voltmètre : i1 = i3 ;  i2 = i4. UAB =-jLw i1  +R1  i2  = R2  i1 -1/ (jCw) i2. 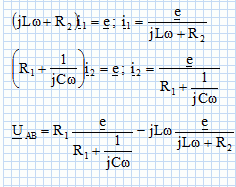Lorsque le pont est équilibré UAB=0. R1(jLw+R2) = jLw (R1+1/(jCw)) R1R2 =L / C. En pratique le pont n'est jamais véritablement équilibré. La cause en est la résistance du bobinage, négligé jusqu'alors et dont on va tenir compte dans cette question. On place en parallèle avec le condensateur variable C, une résistance variable R. Déterminer dans ces conditions la nouvelle expression de l'amplitude complexe UAB. Impédance complexe de l'association R et C en dérivation : admittance complexe Y = jCw +1/R = (jRCw+1)/R ; Z = 1/Y = R / (jRCw+1) Il suffit donc de remplacer le terme 1/( jCw) par R / (jRCw+1) dans l'expression donnant UAB. Quand au terme jLw, il sera remplacer par jLw+r. 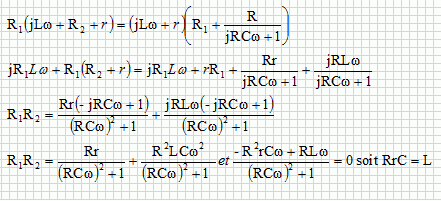A.N : R1=R2 = 1,00 kW ; C = 800 nF ; R = 22,7 kW. 22,7 103 * 800 10-9 r =L ; 0,01816 r = L. 106 =(22,7 103 r +(22,7 103)2L* 800 10-9*3142) / (1+(22,7 103 * 800 10-9 *314)2) 33,51 106 =22,7 103 r +4,064 107 L 33,51 106 =22,7 103 r +4,064 107*0,01816 r ; r = 44,0 W. L = 0,01816 *44,05 =0,800 H. On constate expérimentalement que lorsque la fréquence augmente, le pont se déséquilibre légèrement et qu'il faut réajuster la valeur de la résistance variable R, en la diminuant, pour atteindre le nouvel équilibre. Proposer une interprétation physique à ce phénomène. L'inductance L dépend de la fréquence.

retour -menu