Diagramme binaire eau- NaCl, dureté de l'eau, potentiométrie  capesa 2010.

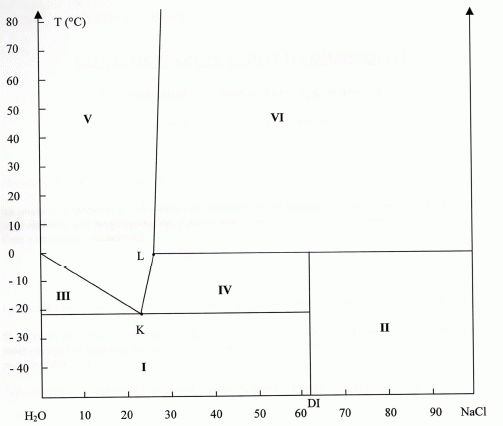
Etude thermodynamique du mélange eau chlorure de sodium. On donne le diagramme binaire H2O - NaCl pour une pression de  1 bar. Dans cette partie on considère la pression constante et égale à 1 bar. La grandeur physique donnée en abscisse est-elle la fraction molaire ou la fraction massique ? Justifier. DI correspond au dihydrate NaCl, 2H2O. Dans le cas d'une fraction molaire, la verticale passant par DI se trouverait à 66,7 % (eau) et 33,3 % ( NaCl). Dans le cas d'une fraction massique :  58,5 *100 / (58,5 + 2*18) = 61,9 % de NaCl : cela correspond au diagramme. Préciser la nature des phases se trouvant dans les différents domaines. I : H2O( s), glace et le dihydrate DI(s).  II : NaCl(s) et le dihydrate noté DI(s). III : H2O( s) et le liquide, la saumure. IV : le dihydrate DI(s) et  la saumure saturée. V : saumure non saturée. VI : sel + saumure saturée. Nommer les points K et L. K : eutectique ; L : péritectique. Le point K, intersection des deux branches du liquidus avec le solidus est appelé point eutectique ; au point eutectique, on a trois phases : liquide + glace pur + dihydrate pur. L : point invariant où coexistent trois phases : le liquide, le dihydrate et le sel NaCl. Préciser le type de fusion du composé NaCl,2H2O ( noté DI). Justifier. La verticale passant par DI n'atteint pas le liquidus : le dihydrate se décompose avant de fondre à une température appelé température de fusion incongruente. Soit un mélange contenant 5,0 g de chlorure de sodium pour 100,0 g de mélange. Déterminer la température pour laquelle ce mélange commence à geler. Donner la nature du solide qui se forme. 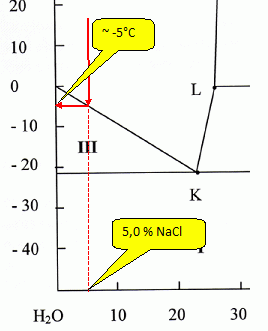La glace se forme à -5°C.   On réalise une solution d'eau salée, de masse 981 g, de fraction massique w =12 % en NaCl, à la température de 25°C. Déterminer les quantités de chlorure de sodium et d'eau nécessaires ( en mol et g ) à la réalisation de ce mélange. mNaCl *100 / mtotale = 12 ; mNaCl = 0,12*981 =117,72 ~1,2 102 g. Soit : 117,72 / 58,5 =2,0 mol NaCl.  mNaCl + mH2O = 981 ; mH2O = 981-117,72 = 863,28 ~8,6 102 g soit : 863,28 / 18 = 47,96 ~48 mol d'eau. Calculer la fraction molaire en NaCl de cette solution. 2,0 / (47,96+2,0) =0,040. On refroidit cette solution jusqu'à -40 °C. Déterminer la nature et la masse des phases en équilibre à -40°C. En déduire la masse de chlorure de sodium dans chacune des phases. Deux phases solides : la glace et le dihydrate NaCl, 2H2O. 117,72 g de NaCl se retrouve dans le dihydrate de masse molaire M = 58,5 +36 = 94,5 g/mol. masse de dihydrate : 117,72 * 94,5 / 58,5 = 190,2 g ~1,9 102 g. masse de glace : 981-190,2 =790,8 g ~ 7,9 102 g. On considère, à la température initiale de 50 °C, un mélange de fraction massique égale à 80 % en NaCl. On refroidit ce mélange jusqu'à la température de -40 °C. Donner l'allure de la courbe d'analyse thermique en précisant la variance, les températures de rupture de phase et la nature des phases présentes pendant les différentes étapes du processus. 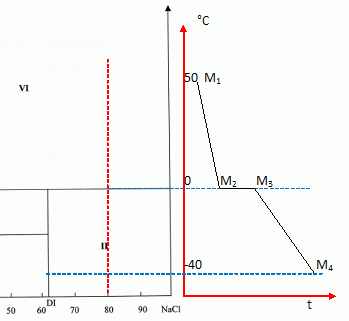M1 M2 : refroidissement saumure saturée et formation NaCl(s) ( variance d'un système binaire à pression constante V = 3-j =1 ) M2 : apparition du dihydrate solide ( variance 0 ). M2 M3 : cristallisation du dihydrate ( variance 0 ) M3  : disparition du liquide ( variance 1) M3 M4 : refroidissement des solides ( variance 1). Détermination de la dureté d'une eau. Une eau dite dure contient des ions calcium et/ou magnésium à une concentration dépassant une valeur fixée par une norme. Elle s'exprime en  degré hydrotimétrique( °TH) et elle est égale à 10 fois la valeur de la concentration en ion calcium et magnésium, lorsque celle-ci est exprimée en mmol/L. Elle est très souvent déterminée par titrage complexométrique à l'aide d'une solution d'EDTA, suivi par colorimétrie ou potentiométrie. L'acide éthylène diamine tétracétique est un tétraacide noté H4Y. Le dosage est réalisé en milieu tamponné pH = pKa4 = 10,2. Donner la définition d'une solution tampon. Une solution tampon modère les variations de pH suite à l'ajout modéré d'un acide fort ou d'une base forte. Lors d'une dilution modérée, le pH d'une solution tampon ne varie pas. On dispose des solutions suivantes NH3, soude, acide chlorhydrique et acide formique. la concentration de ces différentes solutions est égale  à C = 0,100 mol/L. Expliquer comment préparer 100,0 mL d'une solution tampon de pH = 10,2. Couple acide base NH4+aq / NH3aq, pKa = 9,2. pH = pKa + log ([NH3] / [NH4+] ) ; 10,2 = 9,2 + log ([NH3] / [NH4+] ) ; [NH3] / [NH4+] = 10 ; [NH3]= 10 [NH4+]. Mélanger V1 mL de la solution d'ammoniac et V2 mL de la solution d'acide chlorhydrique. Réaction acide base : NH3 + H3O+ = NH4++ H2O. Il se forme V2 C mol d'ion NH4+ ;  il reste  (V1-V2)C mol d'ammoniac. V1-V2 = 10 V2 ; V1 = 11 V2 ; V1 + V2 = 100 ; 12 V2 = 100 ; V2 = 8,33 mL et V1 = 91,67 mL.  Définir puis déterminer le pouvoir tampon de cette solution. Le pouvoir tampon est le nombre de moles d'acide ou de base forte à ajouter à 1 L de solution tampon pour faire varier le pH d'une unité. n moles d'acide fort sont ajoutées à 1 L du tampon précédent :  il se forme n moles d'ion ammonium et il disparaît n moles d'ammoniac. nNH3 = (V1-V2)C-n ; nNH4+ =V2 C + n et le pH prend la valeur 10,2-1 = 9,2. Le pH étant égal au pKa : V2 C + n = (V1-V2)C-n ; n = ½ [(V1-V2)C -V2 C] = ½(V1-2V2)C. n =0,5(91,67-2*8,33)10-3 *0,1 = 3,75 10-3 mol. Le titrage est suivi par potentiométrie. L'électrode de mesure est une électrode au mercure mise en contact d'une solution contenant le complexe [HgY]2- à une concentration CC considérée comme constante. Préciser la nature de l'électrode de référence que l'on peut utiliser. L'électrode de référence utilisée ici est une électrode au calomel saturée (ECS), c'est à dire une électrode de platine (Pt) recouverte de mercure (Hg) sur lequel est déposé du calomel Hg2Cl2. Cette électrode est dite saturée car la solution dans laquelle plonge l'électrode ainsi constituée est une solution aqueuse saturée en chlorure de potassium KCl. Montrer que dans ces conditions, la différence de potentiel E mesurée est fonction  de la concentration Y4-. Donner son expression. E((ECS) = 0,24 V ; constante globale de formation [HgY]2- à 25°C : log b =21,8 ; potentiel standard Hg2+aq/Hg(l) : E° =0,85 V. Hg2+aq + 2e- = Hg(l) ; Emesure = E°(Hg2+aq/Hg(l) ) +0,03 log [Hg2+aq] Hg2+aq +Y4-aq = [HgY]2- aq avec b = [[HgY]2- aq] / ([Hg2+aq][Y4-aq ]) ; [Hg2+aq] = [[HgY]2- aq] /(b [Y4-aq ]) Emesure = E°(Hg2+aq/Hg(l) ) +0,03 log [[HgY]2- aq] /(b [Y4-aq ]) avec [[HgY]2- aq] = CC = constante. Emesure = E°(Hg2+aq/Hg(l) ) +0,03 log [CC /b ] - 0,03 log [Y4-aq ]. E = Emesure- E(ECS) = E°(Hg2+aq/Hg(l) ) +0,03 log [CC /b ]-E(ECS) - 0,03 log [Y4-aq ]. E = constante -0,03 log [Y4-aq ] = B -0,03 log [Y4-aq ]. Donner l'expression et la valeur du potentiel standard du couple [HgY]2- aq/ Hg(l). [HgY]2- aq + 2e- = Hg(l)  + Y4-aq. E = E°([HgY]2- aq/ Hg(l)) +0,03 log ([[HgY]2- aq ] / [Y4-aq]) Or Emesure = E°(Hg2+aq/Hg(l) ) +0,03log(1/b ) +  log [[HgY]2- aq] / [Y4-aq ]) par identification : E°([HgY]2- aq/ Hg(l)) = E°(Hg2+aq/Hg(l) ) +0,03log(1/b )= E°(Hg2+aq/Hg(l) ) -0,03log( b ) E°([HgY]2- aq/ Hg(l)) =0,85-0,03 *21,8 =0,85-0,654 ~0,20 V. L'eau étudiée contient des ions calcium et quasiment pas d'ion magnésium. Lors du titrage, une solution contenant des ions H2Y2- à la concentration C' =0,010 mol/L est ajouté progressivement dans un becher contenant un volume V0 =50,0 mL de l'eau étudiée, un volume VT = 25,0 mL de solution tampon de pH égal à 10,2 et deux gouttes d'une solution assez concentrée du complexe [HgY]2-. Soit V' le volume de la solution ajoutée. Sous quelle(s) forme(s) l'EDTA  prédomine t-il dans la solution ? La solution du becher est tamponnée à pH = 10,2 ; or pKa4 ( HY3- / Y4-) = 10,2. Les formes HY3- et Y4- prédominent. Ecrire l'équation de la réaction de titrage et déterminer la constante d'équilibre correspondante. Ca2+ +H2Y2- + 2NH3 = [CaY]2- + 2NH4+. (1) K = [[CaY]2-][NH4+]2 / ([Ca2+][H2Y2-][NH3]2) Or [NH4+] / [NH3] =10-pH / 10-9,2 =10-pH+9,2  = 0,1. Constante de formation globale de [CaY]2-  : log b' = 10,6. Ca2+ + Y4- = [CaY]2- ; b' =[[CaY]2-] / ([Y4-][Ca2+]) ; [CaY]2-] /[Ca2+] = b'[Y4-] K s'écrit : K = b'[Y4-] * 10-2 / [H2Y2-]. H2Y2-+H2O =  HY3-+  H3O+ ; Ka3 = 10-6,2 = [HY3-][H3O+] / [H2Y2-] HY3-++H2O = Y4- + H3O+ ; Ka4 = 10-10,2 =[Y4-][H3O+] /[HY3-] Ka4  Ka3 =[H3O+]2[Y4-] / [H2Y2-] ; [Y4-] / [H2Y2-]  =Ka4  Ka3 /[H3O+]2; [Y4-] / [H2Y2-] =10-16,4/ 10-2pH =1020,4-16,4=104. K s'écrit : K =102 b'=102 * 1010,6 =1012,6 ~4,0 1012. Donner l'expression de la différence de potentiel E existant entre les électrodes avant l'équivalence en fonction du volume V' ajouté. Donner l'expression de la différence de potentiel E existant entre les électrodes après l'équivalence en fonction du volume V' ajouté. Donner l'allure de la courbe E = f(V'). Potentiel E de l'électrode indicatrice en fonction de [Ca2+] / [[CaY]2-] : Ca2+ + Y4- = [CaY]2- ; b' =[[CaY]2-] / ([Y4-][Ca2+]) soit [Y4-] = [[CaY]2- ]/( b'[Ca2+] ) repport dans E=B-0,03log [Y4-] E=B-0,03log[[CaY]2- ]/( b'[Ca2+] ) et en posant D=B-0,03log b' = constante E= D+0,03 log([Ca2+]/[[CaY]2- ]) On note C la concentration de l'ion calcium dans l'eau : A la date t : [Ca2+] = (CV0-C'V') / Vtotal ; [[CaY]2- ] =C'V' / Vtotal ; [Ca2+]/[[CaY]2- ]= (CV0-C'V') / (CV') E= D+0,03 log(CV0-C'V') / (CV'). [Ca2+] diminue au cours du dosage tandis que [[CaY]2- ] augmente ; log([Ca2+]/[[CaY]2- ]) diminue ainsi que le potentiel E. A l'équivalence :[Y4-] croît rapidement en effet [Ca2+] proche de zéro et [Y4-] =[[CaY]2- ]/( b'[Ca2+] ) or E=B-0,03log [Y4-] : d'où une forte diminution de E. Après l'équivalence, [Y4-] croît lentement du fait de l'ajout d'EDTA ; en conséquence E diminue. [Y4-] =C'(V'-VE) / Vtotal ; E=B-0,03log [Y4-] = B-0,03log [C'(V'-VE) / Vtotal ]. 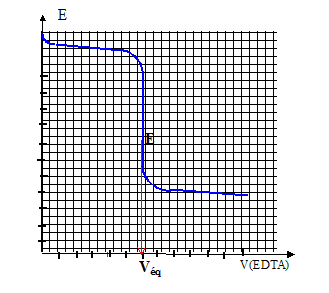Le saut de potentiel obtenu expérimentalement permet de déterminer la valeur du volume équivalent V'E = 11,7 mL. En déduire la dureté D de l'eau en °HT. Conclure. caractère de l'eau douce mi-dure dure °TH jusqu'à 18°TH de 18 à 30°TH plus de 30°TH V'E C' = CV0 ; C = V'E C' / V0  =11,7 *0,010 / 50 =2,34 10-3 mol/L = 2,34 mmol/L soit 23,4 °TH. L'eau est mi-dure, sans doute propre à la consommation.

retour -menu