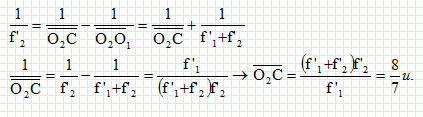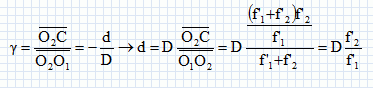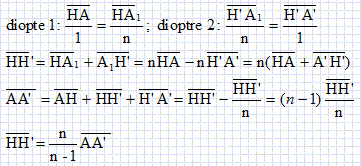Etude d'une paire de jumelles, concours Capes 2010

Aurélie 218/03/10

Etude d'une paire de jumelles, concours Capes 2010.

la paire de jumelles se trouve constituée d'éléments d'optiques assez simples : des lentilles convergentes et divergentes ainsi que des prismes dans la zone masquée.

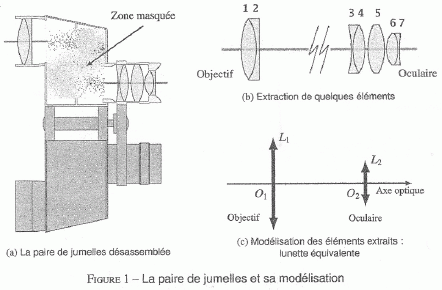
On s'intéresse, en premier lieu, aux groupes de lentilles que nous modélisons, en entrée et en sortie, par des lentilles minces convergentes. On note O₁ et f'₁ ( respectivement O₂ et f'₂) la distance focale image et le centre optique de l'objectif ( respectivement de l'oculaire).
Données du constructeur :

grossissement x7
diamètre objectif 50 mm

angle de visée 7,3°
champ de vision 127 m à 1000 m

distance minimale de mise au point 10,6 m
pupille de sortie 7,14 mm

dégagement oculaire 12 mm
longueur 185 mm

On suppose que f'₂ = u et f'₁ =7 u où u est la longueur de la référence à déterminer, et que le diamètre de l'objectif est le double de celui de l'oculaire. Différents modèles seront proposés et permettront de déterminer trois valeurs différentes de u.
Les éléments du modèle.
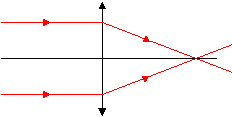
Qu'est ce q'une lentille mince ? Identifier, par leur numéro, les lentilles minces divergentes vissibles sur la figure 1b. Définir l'objectif et l'oculaire.
Lentille : ensemble homogène transparent, souvent réalisé en verre, dont au moins l'une des faces n'est pas plane ; une lentille fait converger ou diverger la lumière.
Mince : l'épaisseur au centre est faible devant le rayon de courbure de ses faces ( dioptres).
Lentilles divergentes : 2, 3 et 7 ( plus épaisse sur les bords qu'au centre).
L'objectif ( la lumière entre par l'objectif , premier élément d'optique de l'instrument ) reçoit les rayons lumineux issus de l'objet ; l'objectif donne de l'objet une image intermédiaire réelle.
L'oculaire ( système optique de sortie de l'instrument ) est situé du côté de l'oeil de l'observateur.
Proposer une méthode de détermination rapide du caractère convergent ou divergent d'une lentille ne portant aucune indication. Justifier à l'aide d'un schéma.
- Au toucher, une lentille convergente est plus épaisse au centre que sur les bords ; une lentille divergente est plus épaisse sur les bords qu'au centre.
- Rechercher l'image d'un objet éloigné sur un écran : pour une lentille convergente, on observe une image dans le plan focal image ; pour une lentille divergente, il n'y a ps d'image.

convergente

divergente

Ces lentilles sont utilisées dans les conditions de l'approximation de Gauss.
Quelles sont ces conditions ? Quelles conséquences en découlent si elles sont respectées ?
L'objet est de petites dimensions etplacé au voisinage de l'axe optique principal. On élimine (utiliser un diaphragme) les rayons lumineux trop inclinés sur l'axe optique principal. Les lentilles, qui fonctionnent dans ces conditions, sont stigmatiques : tout faisceau issu d'un point lumineux donne à la sortie du système optique, un faisceau convergeant en un point, ou semblant provenir d'un point.

La notice précise que " le baryum est la qualité de verre donnant la meilleur réfraction. Grâce à lui, les déformations périphériques et chromatiques de l'image sont limitées "
Comment appelle t-on les aberrations responsables des déformations périphériques ? A quoi sont dues les aberrations chromatiques ?
Aberrations géométriques : distorsion en barillet ou en coussinet.
Aberrations chromatiques : le verre est un milieu dispersif, la célérité de l'onde dépend de la fréquence.
L'objectif et l'oculaire sont réalisés par association de plusieurs lentilles. Pour quelle raison ?
L'association de plusieurs lentilles permet de diminuer les aberrations géométriques et chromatiques.

Encombrement de la lunette équivalente.
La lunette équivalente est réglée de manière à constituer un système afocal.
Préciser ce que cela signifie ? Quel avantage présente ce réglage pour un être humain ?
L'objectif de cette lunette, donne d'un objet AB très éloigné (considéré à l'infini), une image intermédiaire A₁B₁ située entre l'objectif et l'oculaire. L'oculaire qui sert à examiner cette image intermédiaire, en donne une image définitive A'B'. Lorsque cette image définitive est à l'infini, la lunette est dite afocale.

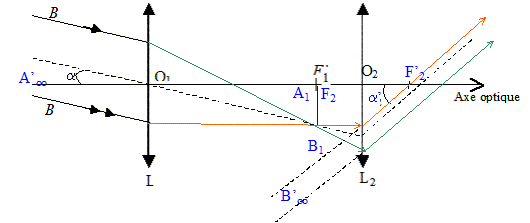
Dans ces conditions l'oeil observe sans accommoder, sans fatigue.
On appelle longueur ou encombrement de la lunette équivalente la grandeur O₁O₂= L₁ entre les centres optiques des deux lentilles.
En déduire L₁ en fonction de f'₁ et f'₂. Pour quelle valeur u₁ de u y a t-il accord avec les données du constructeur ?
L'image intermédiaire, donnée de l'objet par L₁, doit se trouver au foyer image de l'objecif.
L'image définitive étant à l'infini, l'image intermédiaire, objet pour l'oculaire, doit se trouver dans le plan focal objet de l'oculaire.
L₁ = f'₁ + f'₂ = 7 u +u = 8 u ; u₁ = 8 u.
" longueur 185 mm" : 8 u₁ = 185 ; u₁ = 23,1 mm.
Etablir l'expresion algébrique du grossissement, noté G en fonction de f'₁ et f'₂.
L'angle a est orienté dans le sens contraire au sens trigonométrique ; L'angle a' est orienté dans le sens contraire au sens trigonométrique ;
G = a' / a avec tan a = -A₁B₁ / f'₁ ~a et tan a' = A₁B₁ / f'₂ ~ a' ; G =- f'₁ ~f'₂ = -7 u / u = -7.
L'image et l'objet sont de sens contraire.

Le cercle oculaire.
Le cercle oculaire délimite une surface particulière située sans le plan transverse de l'espace image. Il s'agit de l'image par l'oculaire de la monture de l'objectif. La lunette équivalente est réglée de manière à constituée un système afocal.
Pourquoi a t-on intérêt à placer son oeil au niveau du cercle oculaire ?
Le cercle oculaire ( C'D' figure ci-dessous) d'un instrument d'optique est l'image de l'objectif à travers l'oculaire.

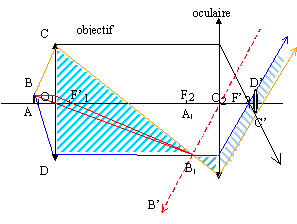
Tous les rayons qui entrent dans le microscope par l'objectif sortent donc par le cercle oculaire.
On doit placer la pupille de l'œil dans ce cercle afin qu'un maximum de lumière entre dans le récepteur, l'oeil.
On note C la position du cercle oculaire sur l'axe optique.
Déterminer littéralement, en fonction de f'₁ et f'₂ la grandeur O₂C.

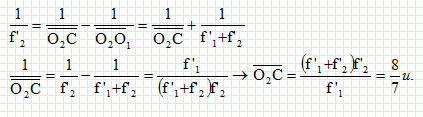
Le constructeur appelle dégagement oculaire ou relief de l'oeil ( RO), la distance entre l'oeil et la première lentille.
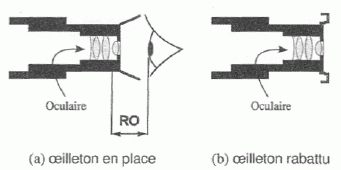
En déduire la valeur u₂ de u. Pourquoi certains observateurs doivent-ils replier l'oeilleton ( figure 2b) ?

RO = 12 mm = 8u/7 ; u₂ = 12*7/8=10,5 mm.
Les porteurs de lunettes ont besoin d'un dégagement oculaire d'au moins 13 mm ( distance supplémentaire entre l'oeil et la jumelle ). Ils rabaissent les oeilletons pour voir correctement le champ de vision.

On note D le diamètre de l'objectif et d celui du cercle oculaire.
Déterminer d en fonction de f'₁, f'₂ et D.
Formule du grandissement transversal pour l'oculaire.

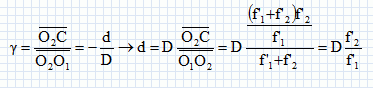
d = D / 7 = 50 /7 = 7,1 mm.
Le constructeur indique que le diamètre du cercle oculaire peut être obtenu en divisant le diamètre de l'objectif par le grossissement.
En déduire la valeur constructeur correspondante et vérifier sa compatibilité avec le calcul précédent.
d = 50/7 = 7,1 mm ( on retrouve la valeur précédente ).
Si elle existe, préciser quelle caractéristique de l'oeil humain pourrait intervenir dans les choix éffectués par le constructeur pour fixer la taile du cercle oculaire.
La pupille de l'oeil s'ouvre au maximum de 2 à 3 mm en plein jour. La nuit , la pupille se dilate jusqu' à 7 mm dans l'obscurité.
Un diamètre oculaire de 7 mm transmet suffisamment de lumière la nuit afin que l'image ne soit pas sombre.

Etude du dispositif redresseur à prismes :
On insère un dispositif redresseur, appelé véhicule, entre l'objectif et l'oculaire. Il peut s'agir d'un système de lentilles ou de prismes. Nous allons nous intéresser à un système à prismes, inventé par Ignazio Porro à la fin du XIX^e siècle.
Que verrait-on à travers la lunette équivalente précédente si on l'utilisait sans dispositif redresseur ?
On observerait une image agrandie mais inversée.
La lunette de Galilée, lunette d'observation terrestre, utilise un objectif convergent et un oculaire divergent : le grossissement étant positif, l'image est agrandie et droite.
Sur le schéma ci-dessous un rayon lumineux monochromatique arrive sous incidence normale sur l'hypothènuse d'un triangle isocèle rectangle, trace du prisme dans son plan de section principale. Toutes les faces de celui-ci sont parfaitement transparentes. l'indice du prisme est supérieur à celui du milieu extérieur.

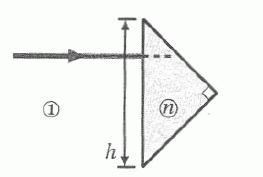
Tracer qualitativement le parcours du rayon lumineux incident s'il est réfracté à la traversée des faces du prisme. Sur le même schéma, représenter le trajet complet de ce rayon lumineux qui, une fois entré dans le prisme, est réfléchi sur les faces du prisme.

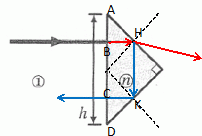
Rouge : réfraction ; bleu : réflexion totale.
AB = BH ; BC = HK ; CK = CD ; dans le cas de la réflexion totale, la distance géométrique parcourue par le rayon lumineux dans le prisme vaut :
BH + Hk + KC = AB + BC + CD = h.
Calculer la valeur limite de l'indice n du prisme assurant la réflexion totale dans les conditions d'éclairage de la figure.
L'indice du gaz dans lequel baigne le prisme est égal à 1,00.
Loi de la réfraction de Descartes en H : n sin 45 = 1,00 sin i₂ avec sin i₂ inférieur ou égal à 1.
n sin 45 inférieur ou égal à 1,00 ; n inférieur ou égal à 1/sin 45 ; n <= 1,41.
Si n est supérieur à 1,41, il y a réflexion totale.
Certaines paires de jumelles sont remplies de diazote gazeux en légère surpression par rapport à l'atmosphère.
Pouquoi le diazote ? Pourquoi en surpression ?
Surpression : l'air, l'humidité, ne peuvent pas rentrer à l'intérieur des jumelles.
Le diazote est un gaz inerte.
Une paire de jumelles contient, dans chaque tube, deux prismes identiques à celui que nous venons de décrire. Nous supposons ici que l'arrangement des prismes ne sert qu'à réduire l'écartement entre les axes optiques des tubes et celui des yeux.
En vous inspirant de la figure 1a, où la zone contenant les prisme a été masquée, proposer un agencement plan des prismes ( qui seront accolés) et des lentilles, permettant d'assurer la réduction de cet écartement.

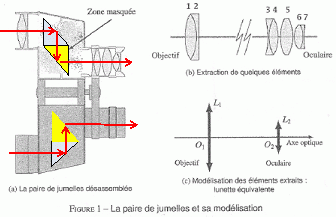
En réalité, la disposition des prismes n'est pas plane ce qui permet de redresser les images dans une paire de jumelles.

Calcul du nouvel encombrement.
La présence des prismes allonge le chemin effectivement suivi par la lumière. Nous allons déterminer cette longueur optique ou encombrement et obtenir une nouvelle valeur u₃ de u.
On s'intéresse au parcours d'un rayon lumineux monochromatique peu incliné dans une lame de verre à faces parallèles de même indice que le prisme.. Le milieu extérieur est assimilé au vide.
Compléter le schéma.
A' image de A à travers la lame de verre.

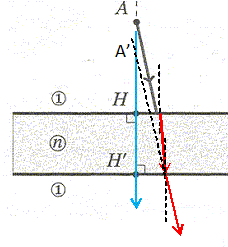
On appelle A₁ le point image d'un point A à travers le dioptre plan et H le projeté orthogonal de A sur le dioptre. Le point A₁ joue le rôle d'objet pour le second dioptre et l'image définitive est A'.
La relation en position du dioptre plan s'écrit :

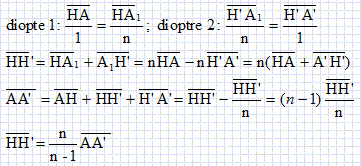
En présence des deux prismes, la longueur optique vaut L = 8u₃+AA' avec HH' =2h.
Exprimer u₃ en fonction de L, h et n.
AA" = 2h(n-1) / n ; u₃ =( L-2h(n-1) / n) / 8.
A.N : L = 235 mm ; h = 25,0 mm ; n=1,67.
u₃ =(235-50*0,67/1,67 ) / 8 = 26,9 mm.
Les modèles proposés ne convergent pas vers une unique valeur de u.
En observant l'association des lentilles (3 ; 4 ; 5 ; 6 , 7 ), identifier la faiblesse du modèle.
u₂ est très différente de u₁ et u₃. L'oculaire est formé de plusieurs lentilles : la largeur de cet ensemble est assez grande ; la distance mesurée depuis la face de sortie est différente de la distance mesurée depuis le centre de la lentille mince équivalente.
On ne peut pas toujours remplacer un ensemble de lentilles par une seule lentille mince équivalente sans prendre en compte les éléments cardinaux du système centré.

menu