Dosage des ions cuivre (II) par complexométrie, concours Capes 2010

Aurélie 16/03/10

Dosage des ions cuivre (II) par complexométrie, concours Capes 2010.

Dosage des ions cuivre (II) dans la bouillie bordelaise à 10 g/L.
La bouillie bordelaise est constituée de 80 % en masse de sulfate de cuivre pentahydraté et de 20 % en masse de chaux éteinte Ca(OH)₂.
Calculer les quantités de matière en hydroxyde de calcium et en sulfate de cuivre pentahydraté dans 1,00 L de bouillie à 10 g/L.
2 g de chaux éteinte ; M(Ca(OH)₂) = 40+2*17 =74 g/mol
n = m/M = 2 / 74 = 2,70 10^-2 mol.
8 g de CuSO₄, 5H₂O; M = 63,5+32+4*16+5*18 = 249,5 g/mol
n = 8 / 249,5 = 3,21 10^-2 mol.
Dans une fiole jaugée de 1,00 L, on introduit 10,0 g de bouillie bordelaise et de l'eau permutée jusqu'au trait de jauge. La solution obtenue n'est pas homogène. On filtre le mélange. Soit S₀ le filtrat. On considèrera que le volume du filtrat est 1,00 L.
Mode opératoire.
Dans un becher de 150 mL introduire :
V₄ = 10,0 mL de la solution S₀
20 mL de tampon acétique à la concentration de 1,0 mol/L de pH = 4,8
80 mL d'eau bipermutée
10 gouttes de complexe HgY^2- à 0,025 mol/L
Une électrode au calomel saturée et une électrode de mercure.
Titrer par une solution d'EDTA disodique ( 2 Na⁺aq+ H₂Y^2-aq ) de concentration C₄ =5,00 10^-3 mol/L.
Tracer la courbe décrivant l'évolution de la différence de potentiel entre les deux électrodes DE en fonction du volume V de solution d'EDTA dissodique versé.

Partie théorique :
Calculer la valeur du potentiel standard du couple HgY^2- /Hg(l).
E°(Hg²⁺ /Hg(l))=0,86 V ; constante de formation globale log b(HgY^2-) = 21,8.
Hg²⁺ aq + 2e^- =Hg(l)
E₁ = E°(Hg²⁺ /Hg(l))+0,03 log [Hg²⁺ aq]
Hg²⁺aq +H₂Y^2-aq = HgY^2-aq+2H⁺aq.
b = [HgY^2-aq][H⁺aq]² /( [H₂Y^2-aq][Hg²⁺aq]) ;
E₁ = E°(Hg²⁺ /Hg(l))+0,03 log([HgY^2-aq][H⁺aq]² /( [H₂Y^2-aq] b).
E₁ = E°(Hg²⁺ /Hg(l))-0,03 log b +0,03 log([HgY^2-aq][H⁺aq]² /( [H₂Y^2-aq]). (1)

HgY^2-aq +2H⁺aq +2e^- = Hg(l) +H₂Y^2-aq
E₂ = E°(HgY^2- /Hg(l)) + 0,03 log ([HgY^2-aq][H⁺aq]² /[H₂Y^2-aq]). (2)
Identifier (1) et (2) : E°(HgY^2- /Hg(l)) = E°(Hg²⁺ /Hg(l))-0,03 log b.
E°(HgY^2- /Hg(l)) =0,86 -0,03 *21,8 =0,206 ~0,21 V.
Exprimer le potentiel de Nernst du couple HgY^2- /Hg(l).
E = E°(HgY^2- /Hg(l)) +0,03 log ([HgY^2-aq][H⁺aq]² /[H₂Y^2-aq]).
Indiquer pourquoi et à quelle condition une électrode de mercure est indicatrice de la concentration en Y^4- et ne dépend que de cette concentration, à température fixée.
[HgY]^2-=Hg²⁺ +Y^4- ; (3) K_d4 = [Y^4-][Hg²⁺] / [[HgY]^2-] soit [Hg²⁺] = K_d4[[HgY]^2-]/[Y^4-]
E = E°(Hg²⁺/Hg) + 0,03 log (K_d4[[HgY]^2-]/[Y^4-]) avec K_d4[[HgY]^2-] = constante notée A
E = E°(Hg²⁺/Hg) + 0,03 log A -0,03log [Y^4-] et en posant B=E°(Hg²⁺/Hg) + 0,03 log A = constante
E=B-0,03log [Y^4-].
La constante de formation globale log b(HgY^2-) = 21,8 est très grande : la concentration [HgY]^2-] peut être considérée comme constante.
Les constante de formation de CaY^2- et CuY^2- sont inférieures.
Déduire de la courbe de dosage des ions calcium (II) par les ions [ HgY]^2- ou cuivre (II) sont dosés en premier.

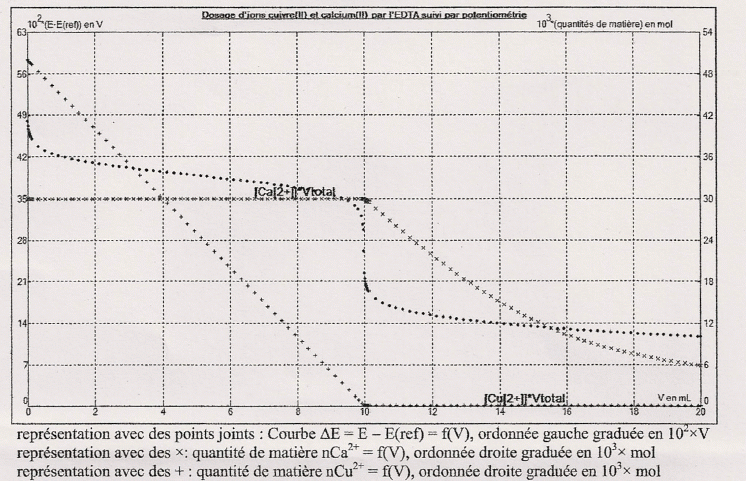
Les ions cuivre (II) sont dosés en premier : la quantité de matière d'ion cuivre (II) décroît jusqu'à s'annuler pour un volume V compris entre 0 et 10 mL alors que celle des ions calcium reste constante entre 0 et 10 mL.
La quantité de matière d'ion calcium décroît pour V supérieure à 10 mL.

Constantes globales de formation : log b(CuY^2-) = 18,8 ; log b(CaY^2-) = 10,7.
Ecrire la réaction de dosage des ions calcium (II) par les ions [ H₂Y]^2-. Calculer sa constante K₁.
Ca²⁺aq +H₂Y^2- aq + 2CH₃CO₂^-aq = CaY^2-aq +2CH₃CO₂Haq.
K₁ =[CaY^2-aq][CH₃CO₂Haq]² / ([Ca²⁺aq][H₂Y^2- aq][CH₃CO₂^-aq]²).
Ca²⁺aq +H₂Y^2-aq = CaY^2-aq+2H⁺aq.
b(CaY^2-)= [CaY^2-aq][H⁺aq]² /( [H₂Y^2-aq][Ca²⁺aq]) ;
CH₃CO₂Haq = CH₃CO₂^-aq +H⁺aq
K_a = [CH₃CO₂^-aq][H⁺aq] /[CH₃CO₂Haq]
K₁ = b(CaY^2-)/ K²_a.
K₁ =10^10,7 / (10^-4,8)² =2,0 10²⁰.
Pour l'ion cuivre (II) on trouverait : K₂ =10^18,8 / (10^-4,8)² =2,5 10²⁸.
K₂ est bien supérieure à K₁ : Cu²⁺aq +H₂Y^2- aq + 2CH₃CO₂^-aq = CuY^2-aq +2CH₃CO₂Haq est prépondérante.
On n'obseve pas de second saut de pH car l'eau doit se réduire avant l'ion calcium.
Donner les propriétés d'une solution tampon.
Une solution tampon modère les variations de pH consécutives à l'ajout d'une petite quantité de base ou d'acide fort, et à une dilution modérée.
En supposant que la concentration molaire volumique en ion cuivre (II) est de 5,0 10^-3 mol/L dans S₀,
montrer par un calcul que la transformation chimique associée au dosage des ions cuivre (II) est quantitative à la première équivalence, compte tenu de l'utilisation d'un tampon acétique de pH=4,8.
K₂ =[CuY^2-aq][CH₃CO₂Haq]² / ([Cu²⁺aq][H₂Y^2- aq][CH₃CO₂^-aq]²).
à pH maintenu à 4,8 : [CH₃CO₂Haq] =[CH₃CO₂^-aq]
K₂ =[CuY^2-aq]/ ([Cu²⁺aq][H₂Y^2- aq]).
Le tableau ci-dessous a été réalisé à partir deu mélange initial correspondant aux quantités de réactifs à l'équivalence ::

avancement (mol)
Cu²⁺aq +H₂Y^2- aq + 2CH₃CO₂^-aq = CuY^2-aq +2CH₃CO₂Haq

initial
0
V₄[Cu²⁺]
C₄V_E
constant
0
constant

en cours
x
V₄[Cu²⁺]-x C₄V_E-x
tampon
x
tampon

équivalence
x_E
V₄[Cu²⁺]-x_E=0 C₄V_E-x_E=0 pH=4,8
x_E pH=4,8

V₄[Cu²⁺]-x_E=C₄V_E-x_E=0 ; V₄[Cu²⁺] = C₄V_E ; [Cu²⁺] = C₄V_E / V₄=5,00 10^-3 * 10 / 10 = 5,0 10^-3 mol/L.
[CuY^2-aq]_E = x_E/ V_total ; [Cu²⁺]_E = [H₂Y^2- ]_E ;
K₂ =[CuY^2-aq]_E / [Cu²⁺]²_E ; [Cu²⁺]²_E = [CuY^2-aq]_E / K₂ ;
Hypothèse : [Cu²⁺]²_E ~5 10^-3 mol/L.
[Cu²⁺]²_E =5 10^-3 /2,5 10²⁸ =2 10^-31 ; [Cu²⁺]_E =4,5 10^-16 mol/L.
L'hypothèse est bien vérifiée ; la transformation est quantitative.

.

menu