Le dipôle RC,  concours agrégation 2009

Lors de l'étude  à l'oscillosope de la réponse à un échelon de tension, il faut veiller au choix de la valeur des composants pour obtenir expérimentalement une visualisation pertinente de la tension crénau et de la réponse aux bornes de C. Comment choisir la fréquence du générateur basse fréquence ? La durée de la charge du condensateur est égale  à 5 fois la constante de temps : 5RC ; la durée "charge +décharge est environ 10 RC. La période de la tension créneau doit être supérieure ou égale à 10RC ; la fréquence de la tension créneau doit être inférieure ou égale à 1/(10RC). 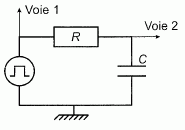Quel est le schéma équivalent de l'entrée d'un oscilloscope à cette fréquence ?  On utilise un oscilloscope dont les caractéristiques d’entrée sont indiquées :" 106 ohms, 25 pF". Dans la suite, on désigne par R0 et C0 la résistance et la capacité correspondantes. 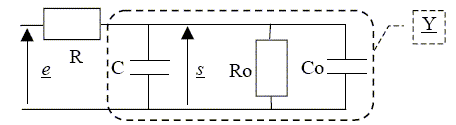Cet appareil, branché sur le filtre précédent, correspond ainsi au circuit suivant : Gain en tension à basse fréquence, noté H0. A basse fréquence, un condensateur se comporte comme un interrupteur ouvert. Admitance d'entrée de l'oscilloscope : Y = jC0w + 1/R0 à basse fréquence : Y0 =1/R0 ; Z0 = R0. H0 = s / e = R0/ (R+R0). L'entrée de l'oscilloscope est équivalente  à une résistance de valeur 1 MW. Que se passe t-il si la résistance R du circuit est très élevée ? En régime permanent, la tension aux bornes du condensateur est : ER0/ (R+R0). Lors de la charge ( ou de la décharge) la constante de temps du circuit vaut  : RR0 / (R+R0) C. Donner l'ordre de grandeur de la valeur limite Rmax de cette résistance. Rmax doit être  de l'ordre de la résistance de l'entrée de l'oscilloscope, c'est à dire 1 MW. Quel est le schéma équivalent d'un générateur basse fréquence ? Un GBF est équivalent à un générateur de tension idéal en série avec une résistance notée RGBF. Que se passe t-il si la résistance du cirduit est très faible ? Donner l'ordre de grandeur de la valeur limite Rmin. La  tension d'entrée est un créneau déformé. La constante de temps du circuit est (R+RGBF) C. Rmin =RGBF ~ 50 W. L'étude expérimentale peut se faire à l'aide d'un système informatique d'acquistion de données. Quelles sont les réglages à effectuer pour avoir une  acquisition convenable de la tension aux bornes du condensateur en réponse  à un échelon de tension d'amplitude E. E = 6 V ; r = 10 kW ; C = 10 nF. La constante de temps du circuit est RC = 104 * 10-8 = 10-4 s = 0,1 ms. Durée de l'acquisition : 1 ms ; temps entre deux mesures : 1 µs. L'acquisition se fait sur le signal d'entrée On étudie le régime sinusoïdal forcé des circuit RC. Quelles méthodes donner aux élèves pour qu'ils puissent déterminer qualitativement la nature du filtre avant de commencer les calculs de la fonction de transfert ? La tension de sortie est la tension aux bornes du condensateur. En très basses fréquences, le condensateur se comporte comme un interrupteur ouvert : la tension de sortie est égale à la tension d'entrée. En hautes fréquences le condensateur est équivalent  à un interrupteur fermé : la tension de sortie est nulle. Le circuit est donc un filtre passe bas. Déterminer l'expression de la fonction de transfert du circuit série RC, la tension de sortie étant prise aux bornes de C. Les grandeurs soulignées sont des nombres complexes. Z : impédance complexe de l'ensemble RC série : Z = R+1/jCw ; e = Z i ; s = i /jCw ; s / e =1/ ( Z jCw ) =1 / ( 1 + jRCw). H= 1 / ( 1 + jRCw). 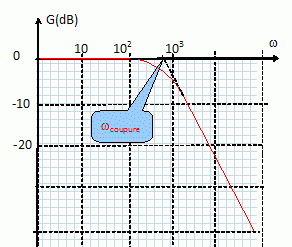Tracer le diagramme de Bode du filtre précédent ; on se limitera au tracé du gain. Quelles sont les caractéristiques de ce filtre ? Le module de H est : H = 1/ [1+(RCw)2 ]½. gain G = 20 log H = -10 log [1+(RCw)2 ] Aux basse fréquences G est équivalent  à : G~0 ( asymptote horizontale) En hautes fréquences, G est équivalent  à : G ~ -20 log (RCw) ( asymptote oblique de pente -20 dB par décade. Pulsation  de coupure  à -3 dB : -3 = -10 log [1+(RCw)2 ] ; 0,3 = log [1+(RCw)2 ] ; 100,3 = 2 = 1+(RCw)2. RCw =1 ; wc =1/ (RC). Il s'agit d'un filtre passe bas. Tracer pour ce même circuit, la tension aux bornes du condensateur en réponse à un échelon de tension. Comment montrer aux élèves que cette réponse permet de trouver la nature du filtre ?     Représenter graphiquement T(r) en fonction de r. Le câble est-il en compression  ou en tension ? Quel est le risque lié à cette situation ? 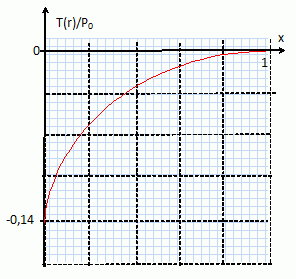La tension étant négative, le câble travaille en compression : il y a un risque d'effondrement de ce dernier. Pour remédier à ce problème on envisage un câble qui dépasse l'orbite géostationnaire ( dont la longueur est supérieure à RS-RT). Comment est dirigé le poids apparent d'un élément de longueur du câble situé à r >RS ? 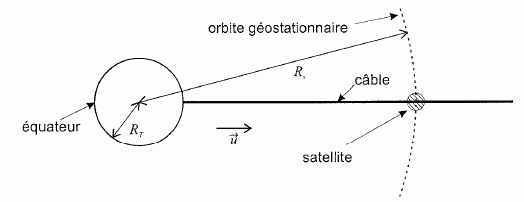dP(r) représente le poids apparent d'un élément de longueur du câble : dP(r) = r S g0RT2( 1/ r2 -r/RS3) dr. dP(r) = r S g0RT2 r ( 1/ r3 -1/RS3) dr ; r est supérieur  à RS : le terme 1/RS3 lié à la force centrifuge l'emporte sur le terme 1/ r3 lié au poids. dP(r)  a le sens du vecteur u. Montrer que si le câble dépasse une certaine distance R0, il est en tension sur toute distance r. Quel est alors le poids apparent du câble ? Dans le référenttiel terrestre, le câble est en équilibre sous l'action de son poids apparent et de l'action exercée par la Terre ( point de fixation ) sur le câble  -T(RT). -T(RT) +Papp = 0 ; Papp = T(RT). Si le poids apparent est positif, T(RT) est positif ( câble tendu).  A l'extrémité libre du câble la tension est nulle : Papp = T(R0)=0. 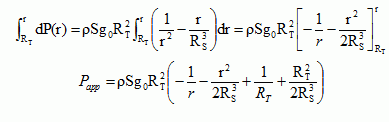Exprimer R0 en fonction de RS et RT. 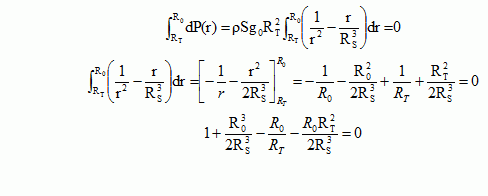Hypothèse : R0 >> RS, les termes  1 et R0RT2/(2RS3) sont négligeables : R0 ~[2RS3 / RT]½. A.N : R0 ~[2*420003 / 6400]½~ 1,5 105 km ( l'hypothèse est vérifiée ). 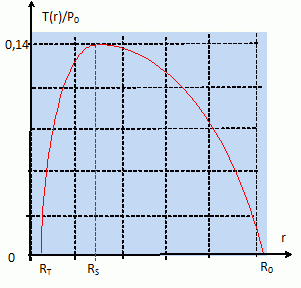Représenter graphiquement T(r) en fonction de r pour un câble de longueur R0-RT. A quelle distance, le maximum Tmax de T(r) est-il atteint ? Donner l'expression de Tmax. T(r) passe par un extrémum quand dP(r) = 0, c'est à dire pour r = RS. T(r) est nulle  pour r = R0 et pour r = RT : il s'agit donc d'un maximum.   Câble de section variable. On enviseage ici un câble de section variable S(r) de longueur supérieure à R0-RT. On définit la contrainte s(r) du  câble au point r par : s(r) = T(r) / S(r). Pour un matériau donné, la contrainte ne doit pas excèder une valeur critique sc sous peine d'entraîner des déformations irréverssibles conduisant éventuellement  à sa rupture. Montrer que pour optimiser la masse du câble, on doit faire varire sa section de façon  à avoir, pour tout r, s(r) =sc. Dans la suite on suppose cette condition réalisée. En choisissant la section S(r) = T(r) / sc, la contrainte critique n'est pas dépassée quel que soit r et la masse est optimisée. Montrer que S(r) satisfait l'équation différentielle : D'une part : dT(r) = r S g0RT2 r ( 1/ r3 -1/RS3) dr ; d'autre part : S(r) = T(r) / sc. dS(r) = r S g0RT2 r ( 1/ r3 -1/RS3) /sc dr dS(r) / S(r)= r  g0RT2 r ( 1/ r3 -1/RS3) /sc dr = RT2 / h   ( 1/ r2 -r / RS3) dr. dS(r) / S(r) est sans dimension : donc h a la dimension d'une longueur. Inégrer l'équation ci-dessus : on note SS la section du câble au niveau de l'orbite géostationnaire. Représenter schématiquement la dépendance de S(r)  avec r. En déduire le rapport d'aspect du câble SS / ST = exp(0,775RT / h ) ST est la section du câble  à la surface de la Terre. Comment varie la tension T(r) ?   T(r) =S(r)  sc. La tension T(r) varie comme la section S(r). Représenter SS/SR en fonction de h pour h compris entre 50 km et 10000 km. Choix du matériau. matériau acier Kevlar nanotubes r (kg m-3) 7800 1450 1300 sc (x109 N m-2) 1 3,5 100 E (x109 N m-2) 200 30 1000 E module de Young ; s = E dl /l où dl /l  est l'allongement relatif du matériau sous la contrainte s. Calculer h pour chaque matériau. Commenter. h = sc/(rg0) ; hacier =109 / (7800*9,8) =1,3 104 m = 13 km. hKevlar =3,5 109 / (1450*9,8) =2,46 105 m = 246 km ; hnanotube =100 109 / (1300*9,8) =7,85 106 m = 7850 km Rapport d'aspect du câble. SS / ST = exp(0,775RT / h ) acier : SS / ST =5 10165 ; Kevlar : SS / ST =5,7 108 ; nanotube : SS / ST =1,88 ( techniquement réalisable ) Le seul matériau envisageable est les nanotubes. Quel est l'allongement relatif du câble sous contrainte critique ? Commenter. dl /l  = sc / E ; acier : 1/200=0,005 ; Kevlar : 3,5/30 =0,12 ; nanotubes : 100/1000 = 0,10. L'acier  possède un allongement relatif  bien inférieur au Kevlar et aux nanotubes. On cherche  à lever le long du câble une masse de 10 tonnes. On se donne comme critère de fonctionnement de l'ascenseur que le poids de cette masse au niveau de la Terre ne doit pas excéder T(RT) / 10. Evaluer S(RT) et S(RS) pour les différents matériaux. Commenter. Poids de la charge à la surface de la terre : m = 104 kg ; g0 ~ 10 m s-2 ; mg0 = 104*10 = 105 N ; T(RT)  = 10 * 105 = 106 N. D'une part : ST =T(RT)/ sc  et d'autre part : SS  = ST exp(0,775RT / h ). matériau acier Kevlar nanotubes ST (m2) 106 /109 = 10-3. 106 /(3,5 109 ) = 2,8 10-4. 106 /1011 = 10-5. SS (m2) 5 10165 *10-3 ~5 10162. 2,8 10-4 *5,7 108= 1,6 105. 1,9 *10-5. Le seul matériau envisageable est les nanotubes.

retour -menu