Soit le noyau 1 de symbole126X et le noyau 2 de symbole116Y.
Ces noyaux ont comme énergies de liaison respective EL1 =
91,6 MeV et EL2 = 73,0 MeV.
A. Ces noyaux sont
isobares.
Faux.
Deux noyaux isobares possèdent
le même nombre de nucléons ; le noyau 1 en compte 11 tandis que le
noyau 2 en compte 12.
B. L'énergie de liaison du noyau 1
vaut 1,47 10-11 J. Vrai.
91,6 *1,6 10-13 = 1,47 10-11
J.
C. Ces deux noyaux sont isotopes.Vrai.
Ces deux noyaux possèdent le
même nonbre de charge, c'est à dire 6, et des nombres de neutrons
différents.
D. Le noyau le plus stable est le
noyau 2. Faux.
Energie de liaison par nucléon
: EL1 / 12 =91,6 / 12 =7,63 MeV / nucléon ; EL2 / 11 =73,0 / 11 =6,64 MeV /
nucléon ; le noyau le plus stable possède la plus
grande énergie de liaison par nucléon.
On
considère le spectre d'émission de l'atome d'hydrogène. On ne
s'intéresse qu'aux radiations de la série de Balmer qui correspondent
aux transitions électroniques des niveaux n=3, 4, 5, 6 vers le niveau
n=2. ( Le niveau n=1 correspond à l'état fondamental ).
A. Dans l'atome
d'hydrogène, l'énergie exprimée en eV, d'un niveau n est donnée par la
relation En = -13,6 / n2. Vrai.
B. Toutes les radiations
correspondant aux transitions considérées se situent dans le domaine
visible. Vrai.
C. L'énergie de la
radiation la plus énergétique de celles étudiées est égale à 3,02 eV. Vrai.
E2 = -13,6 / 4 = -3,4 eV ; E6 =
-13,6 / 36 = -0,378 eV ; E6 -E2 =
-0,378 + 3,4 =3,02 eV.
D. La radiation la plus
énergétique de la série se nomme raie "La". Faux.
La moins énergétique se note Ha
; transition du niveau n=3 vers le niveau n=2.
|
Soit un tube à
rayons X alimenté par une tension accélératrice de U =50 kV.
A. Les rayons X sont émis au niveau
de la cathode. Faux.
Les
rayons X sont émis par l'anode.
B. La plus petite
longueur d'onde des radiations émises est égale à 2,5 10-12 m.
Vrai.
Energie
maximale : e U = 1,6 10-19 * 50 103 = 8,0 10-15
J.
l = hc / E = 6,63
10-34*3 108 / 8,0 10-15 =2,5 10-12
m.
C. La
partie continue du spectre correspond au rayonnement de freinage. Vrai.
D.
Le rayonnement de freinage résulte d'une interaction photons / noyaux
des atomes de la cible. Faux
interaction
électron / noyaux des atomes de la cible.
|
On considère une onde ultrasonore de
fréquence 2 MHz.
A. Dans l'air, cette
onde ultrasonore va se déplacer plus vite qu'une onde de même nature
appartenant au domaine de l'audible. Faux
B. La célérité de cette
onde est plus grande dans l'air que dans l'eau.
Faux.
La célérité est de l'ordre de 300 m/s dans
l'air et 1500 m/s dans l'eau.
C.
La longueur d'onde du signal considéré se propageant dans l'air reste
la même dans l'eau. Faux.
La
célérité et la longueur d'onde dépendent du milieu de propagation.
D.
On utilisera cette fréquence de 2 MHz plutôt qu'une fréquence de 10 MHz
pour explorer par échographie un organe profond. Vrai.
Effet Compton
et autres interactions.
Décrire brièvement l'interaction par effet Compton. Illustrer vos propos par un schéma et donner le bilan énergétique.
Lorsqu'un photon X passe à proximité d'un électron périphérique peu lié à
l'atome, l'énergie du photon est en partie transmise à l'électron : ce dernier
est arraché de l'atome et s'échappe avec une certaine énergie cinétique. Le
reste de l'énergie se retrouve sous la forme d'un photon X de direction
différente et d'énergie inférieure.
La probabilité d'interaction par un effet Compton ne dépend pas du numéro
atomique.
L'effet Compton est prépondérant dans les tissus organiques avec des photons
X de grande énergie.
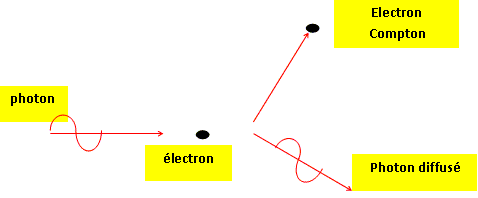
Un photon d'énergie E interagit par effet Compton avec un
électron. Il projette cet électron en lui communiquant une énergie cinétique Ec, le reste étant emporté par un photon diffusé d'énergie E' faisant un
angle q avec la direction
du photon incident.
La conservation de l'énergie conduit à : E = Ec+E'.
Au cours de cette interaction, on montre que la différence entre l', longueur d'onde du photon diffusé, et l, longueur d'onde du photon incident vaut :
Dl =l'-l = h(1-cosq) / (mec)
où q correspond à la valeur de l'angle entre la direction du photon incident et celle du photon diffusé, et me la masse de l'électron.
Deux cas extrèmes peuvent se présenter : cas d'un choc frontal et cas d'un choc tangentiel.
Dans lequel de ces deux cas l'énergie reçue est-elle maximale ?
L'énergie reçue par l'électron est maximale si Dl est maximale, soit (1-cosq) = 2 ou q = 180°.
Quel est la valeur de q dans le cas d'un choc frontal ? 180°.
Le photon incident a une énergie Ei = 500 keV. On suppose qu'il interagit par effet Compton.
Calculer la longueur d'onde correspondant à ce photon incident.
l = hc /E = 6,63 10-34*3 108 / (500*103*1,6 10-19) =2,4863 10-12 ~2,49 10-12 m.
Calculer la longueur d'onde l' associée au photon diffusé dans le cas d'un choc frontal si Dl = 4,85 10-12 m.
l' = Dl +l =4,85 10-12 +2,4863 10-12 =7,3363 10-12 m ~7,34 10-12 m.
Vérifier que Ed, l'énergie du photon diffusé vaut 170 keV.
Ed = hc / l' = 6,63 10-34*3 108 / 7,3363 10-12 =2,71 10-14 J
2,71 10-14 / 1,6 10-19 =1,69 105 eV ~169 keV.
On sintéresseaux autres types d'interactions photons-matière.
Schématiser
les zones de prédominance des différents effets en fonction de
l'énergie des photons incidents et du numéro atomique du milieu traversé.
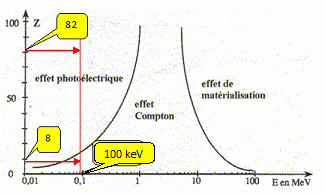
Un photon d'énergie 100 keV interagit avec de l'eau ( Z associé = 8 ). Dans ces conditions, quel type d'interaction prédomine ?
L'effet Compton ( voir schéma ci-dessus ).
Un photon d'énergie 100 keV interagit avec du plomb ( Z =82 ). Dans ces conditions, quel type d'interaction prédomine ?
L'effet photoélectrique ( voir schéma ci-dessus ).
Quelle
énergie minimale doit avoir un photon pour provoquer une
matérialisation ? Que représente cette énergie ? Justifier par un calcul.
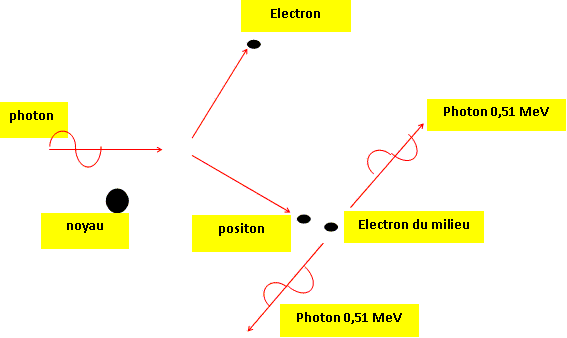
Le photon ( d'énergie supérieure à 1,02 MeV) disparaît : il donne naissance à
un électron et à son anti-particule, le positon.
|
Le coefficient d'atténuation linéique global des photons de 100 keV traversant l'eau vaut µ=0,17 cm-1.
Quel est le pourcentage du nombre de photons transmis apès la traversée de 2,0 cm d'eau ?
Loi de l'atténuation d'un faisceau
monochromatique par un objet de densité
uniforme :
I = I0 exp
(-µL)
I0 : flux de rayons X incident ; I
:flux de rayons X sortant ; µ : coefficient
d'atténuation linéique du milieu ; L
: épaisseur du milieu traversé.
I / I0 = exp( -0,17*2,0) = 0,71 ( 71 %).
Calculer la valeur de la couche de demi-atténuation ( C.D.A) de ce milieu dans ces conditions.
µ C.D.A = ln 2 ; C.D.A = ln 2 / µ = 0,693 / 0,17 = 4,08 ~ 4,1 cm.
|
|
|
|


