Chimie :
L’Hermione
est une frégate qui a transporté La fayette aux Etats Unis. Construite
en 1779, elle a coulé en 1793 au large des côtes françaises. Les canons
et l'ancre de cette épave ont été remontés à la surface en 2005 et ont
subi un traitement élecrolytique de 45 mois avant leur xposition à
l'air libre. Un technicien du laboratoire chargé du traitement explique
:
" Exposées à l'air, ces pièces gorgées de sel serait victimes de la
corrosion si elles ne bénéficiaient d'un traitement par électrolyse qui
dure plusieurs années et permet dans un premier temps, de libérer
l'objet de la gangue de sédiments et coquillages qui l'emprisonne, puis
de supprimer les traces de sel, avant de le sécher et traiter
pour qu'il se conserve parfaitement."
A la sortie de l'eau, les vestiges sous-marins sont recouverts
de concrétions atteignant pluisues centimètres d'épaisseur formant une
épaisse croûte ( on parle d'une gangue ) autour des objets.
Le schéma de principe de traitement est le suivant :
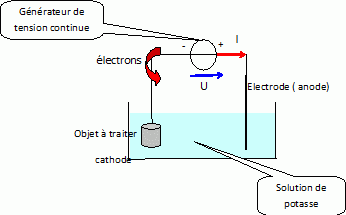
Le bain électrolytique est une
solution d'hydroxyde de potassium. L'hydroxyde de potassium est une
base forte.
Expliquer
ce qu'est une base forte. Ecrire le bilan de
la réaction de dissolution de l'hydroxyde de potassium dans l'eau.
Une base est une espèce susceptible de gagner un proton H+.
La réaction d'une gase forte avec l'eau est totale.
KOH(s) = K+aq + HO-aq.
La
réaction se déroulant à l'électrode reliée à la borne positive du
générateur est-elle une oxydation ou une réduction ? Justifier.
L'électrode
reliée à la borne positive du générateur est une anode. Une oxydation
se déroule à l'anode, tandis qu'une réduction se produit à la cathode.
|
A
l'une des électrodes, on observe un dégagement de dihydrogène. La
pression exercée par le dihydrogène permet de décoller plus facilement
la gangue.
Quelle
est l'équation de la réaction électrochimique qui se produit à cette
électrode ?
Réduction de l'eau en dihydrogène à la cathode négative selon :
2H2O (l) + 2e- = H2(g) + 2HO-aq.
Ecrire
le bilan global de la réaction qui a lieu lors de la restauration de
ces vestiges sachant que les couples oxydant / réducteur sont : H2O (l) / H2(g) et Cl2(g) / Cl-aq.
Oxydation des ions chlorure en dichlore à l'anode positive suivant : 2Cl-aq = Cl2(g) + 2e-.
Bilan : 2Cl-aq + 2H2O (l) = Cl2(g) +H2(g) + 2HO-aq.
|
Electricité
:
On
considère une installation électrique alimentée par un réseau triphasé
équilibré 230 V / 400 V, 50 Hz. Cette installation comporte :
- Deux moteurs asynchrones triphasés consommant chacun une puissance
active PM =30 kW avec un facteur de puissance égal à
cos fM =0,75.
- Trois fours triphasés consommant chacun une puissance active PF
= 5 kW avec un facteur de puissance égal à cos fF =1,00.
Déterminer
les puissances réactive et apparente d'un moteur et d'un four.
Moteur :
- puissance apparente SM = PM / cos fM =30 / 0,75 = 40 kVA.
- puissance réactive : QM = PM * tan fM =30*0,882 =26,46
~26,5 kvar.
Four :
- puissance apparente SF = PF / cos fP =5 / 1 = 5 kVA.
- puissance réactive : QF = PF * tan fF =5 *0 =0 kvar.
Déterminer les puissances active Ptot, réactive Qtot
et apparente Stot consommées par l'ensemble en
fonctionnement.
|
puissance
active
kW
|
puissance
réactive
kvar
|
puissance
apparente
kVA
|
un
moteur M
|
30
|
26,5
|
40
|
un
four F
|
5
|
0
|
5
|
ensemble
2 moteurs + 3 fours
|
30*2+15=75
|
26,46*2=52,9~53
|
(752
+ 532) ½=91,8 ~92
|
Déterminer
le facteur de puissance de cette installation :
cos ftot = Ptot
/ Stot = 75/92=0,817 ~0,82.
Déterminer
l'intensité efficace I du courant de la ligne qui alimente cette
installation.
I = Stot / ( 3½U) = 92 000 / (1,732*400) =132,8
~133 A.
On cherche à relever le facteur de puissance à cos f'tot =0,98 afin de satisfaire les
conditions demandées par le fournisseur d'énergie électrique. Pour cela
on place une batterie de trois condensateurs montés en triangle ayant
chacun une capacité C.
Donner,
sans démonstration, la valeur de la puissance active consommée par un
condensateur puis par la batterie de condensateur.
Un condensateur ne consomme pas de puissance active, mais de la
puissance réactive -3½Cw
U2.
Déterminer
la nouvelle valeur I' de l'intensité efficace du courant qui alimente
l'ensemble.
I = Stot / ( 3½U) avec Stot
= Ptot / cos ftot
; I = Ptot / ( 3½Ucos ftot)
I' = S'tot / ( 3½U) avec S'tot
= Ptot / cos f'tot
;
I' =Ptot / (3½U cos f'tot)
; I' =I cos ftot/
cos f'tot ;
I' = 132,8 *0,817 / 0,98 = 110,7 ~111 A.
En
déduire un intérêt du relèvement du facteur de puissance.
La nouvelle valeur de l'intensité est près de 20 % inférieure à la
valeur initiale ( sans relèvement du facteur de puissance).
Or les pertes en ligne par effet Joule sont proportionnelles à
l'intensité : en conséquence, relever le facteur de puissance diminue
les perte par effet Joule en ligne.
Principe du réfrigérateur :Le principe du réfrigérateur à compression est indiqué ci-dessous :
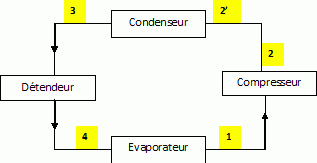
Le fluide utilisé est l'ammoniac et le cycle décrit par un kilogramme
de fluide est schématisé dans le diagramme entropique ( T, S) sur
lequel la courbe de saturation est représenté en pointillés (
l'entropie masique S est en abscisse, la température T en ordonnée).
L'état 5 est un état fictif de l'ammoniac car il ne fait pas partie du
cycle décrit par ce fluide. Dans l'état 5, l'ammoniac serait dans un
état de liquide saturé.
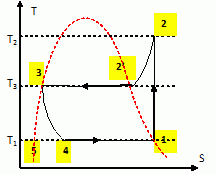
l'ammoniac sort de l'évaporateur dans l'état 1 ( T1 = 263 K, P1
= 2,9 bar) sous forme de vapeur saturante sèche. Il pase dans le
compresseur où il subit une compression adiabatique réversible. Il sort
du compresseur ( à l'état de vapeur surchauffée) dans l'état 2 ( T2 , P2 = 10,7 bar)
En assimilant l'ammoniac gazeux à un gaz parfait, exprimer littéralement puis calculer la température T2 en fin de compression. On donne g = 1,29.
Pour une transformation adiabatique réversible : P1(1-g) / g T1 = P2(1-g) / g T2 avec (1-g) / g = (1-1,29) / 1,29 = -0,225.
T2 = T1 [P1 / P2](1-g) / g ; T2 = 263[2,9 / 10,7 ]-0,225 =353 K.
Dans la suite de l'exercice on prendra T2 = 353 K.
De 2 en 2', l'ammoniac se refroidit de manière isobare de la température T2 à la température T3 = 300 K.
En assimilant l'ammoniac gazeux à un gaz parfait, exprimer puis calculer l'énergie Q22' échangée sous forme de chaleur par 1 kg de fluide, avec le milieu extérieur, au cours de ce refroidissement. Commenter le signe.
On donne capacité thermique massique moyenne de l'ammoniac gazeux, à pression constante entre les températures T2 et T3 : Cp =2,75 kJ mol-1 K-1.
Q22' = Cp(T3-T2) =2,75 (300-353) = -146 kJ kg-1.
Le signe moins traduit le fait que le fluide cède de l'énergie au milieu extérieur.
|
L'ammoniac
est dans l'état 2' sous forme de vapeur saturante sèche. Il pénètre
alors dans le condenseur où il se liquéfie, à la pression P3 = P2 et à la température T3. A la sortie du condenseur en 3, le fluide est à l'état de liquide saturé.
Calculer l'énergie Q2'3 échangée sous forme de chaleur par 1 kg de fluide, avec le milieu extérieur au niveau du condenseur.
On donne l'enthalpie massique de vaporisation de l'ammoniac à la température T3 = 300 K : Lv = 1,16 103 kJ kg-1.
Q2'3 = - m Lv = -1*1,16 103 kJ kg-1= -1,16 103 kJ kg-1.
Le liquide pénètre alors dans le
détendeur. De 3 à 4, il subit une détente isenthalpique au cours de
laquelle une partie du liquide se vaporise. La vaporisation du liquide
restant va se terminer dans l'évaporateur à la pression P1 et à la température T1.
Calculer la masse de liquide mliq qui se vapoise dans l'évaporateur lorsque 1 kg de fluide décrit le cycle.
On donne : h1 = 1449 kJ kg-1 ; h3 = h4 = 324 kJ kg-1 ; h5 = 153 kJ kg-1 ; on note x le titre en vapeur :
x = (h4-h5) / (h1-h5) =(324-153) / ( 1449-153) = 0,132 ½0,13 ( 13 %).
La masse du liquide est égale à 0,87 kg.
Calculer l'énergie Q41 échangée sous forme de chaleur par cette même masse liquide, avec le milieu extérieur, au niveau de l'évaporateur.
Chaleur latente de vaporisation de l'ammoniac à la température T1 : h1-h5.
Q41 = mliq (h1-h5) = 0,87 ( 1449-153) = 1128 kJ ~1,13 103 kJ.
Efficacité du réfrigérateur.
Exprimer puis calculer l'énergie totale Qtot échangée sous forme de chaleur par 1 kg de fluide avec le milieu extérieur, au cours du cycle.
Qtot = Q22' + Q2'3 + Q41 = -146-1,16 103 +1128 = -178 kJ kg-1.
A l'aide du premier principe de la thermodynamique, exprimer puis calculer l'énergie Wtot échangée sous forme de travail mécanique par 1 kg de fluide avec le milieu extérieur, au cours du cycle. Commenter le signe.
Qtot + Wtot = 0 ; Wtot = 178 J kg-1.
La valeur étant positive, le fluide reçoit du travail de la part du milieu extérieur : il s'agit d'un cycle récepteur.
Où doit-on placer le compartiment à refroidir ? Justifier.
Le fluide doit recevoir de la chaleur de la part des aliments à
refroidir : l'évaporisation d'un liquide prélève de la cjleur au
compartiment à refroidir. Ce compartiment doit être en contact avec
l'évaporateur.
Déterminer
l'expression littérale de l'efficacité théorique e de la machine
frigorofique et vérifier que sa valeur est de l'ordre de 6,3.
efficacité théorique = énergie prélevée au compartiment à refroidir divisée par le travail mis en oeuvre.
e = Q41 / Wtot =1128 / 178 = 6,3.
|
|


