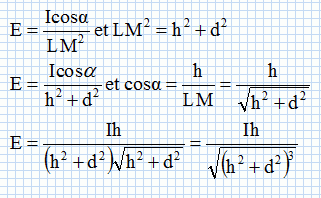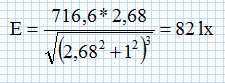Etude photométrique d'un tube solaire.
(7 points).
On donne l'expression de la loi de Bouguer : E = I cos a / LM2.
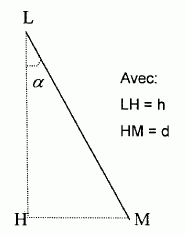
Afin d'améliorer l'éclairage d'une pièce, on peut faire pénétrer la
lumière du jour par la toiture grâce à un tube solaire qui est
constitué d'un dôme capteur de lumière sur la toiture, prolongé par un
tube de transmission qui aboutit à un diffuseur dans la pièce.
On cherche à savoir à quelle hauteur il faut placer le diffuseur de
manière à ce que l'éclairage apporté soit comparable à celui d'une
lampe de 75 W d'efficacité lumineuse k = 30 lm W-1.
Lumière solaire.
Rappeler les valeurs extrèmes des longueurs d'onde des radiations du spectre visible.
Placer sur un axe orienté en longueur d'onde les domaines du visible, de l'ultra-violet et de l'infrarouge.
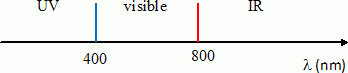
Etude de la lampe de 75 W.
On considère que la lampe émet uniformément depuis le point L dans un angle solide W = 2 p stéradians.
Calculer le flux lumineux F qu'émet cette lampe.
En déduire l'intensité lumineuse I de celle-ci.
F = 75*30 =2250 lm.
I = F / p = 2250/3,14 =716,6 ~7,2 102 Cd.
Calculer la hauteur h à laquelle doit être placée la lampe pour que l'éclairement en H soit de E = 100 lx.
E = I / h2 ; h = (I / E )½ =(716,6 / 100 )½ =2,68 ~2,7 m.
|
En utilisant la loi de Bouguer, montrer que l'éclairement en M s'écrit :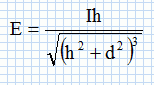 . .
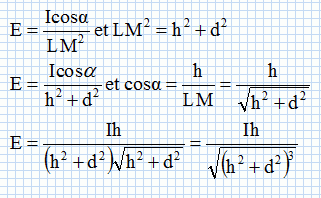
|
Calculer l'éclairement E en M tel que HM = 1,0 m.
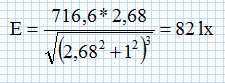
Etude du tube solaire.
En admettant que l'on puisse considérer que le diffuseur du tube est
une source ponctuelle qui émet uniformément dans un angle solide W=2p avec une intensité lumineuse I = 400 Cd par beau temps,
calculer
la hauteur h' à laquelle il faudrait le placer afin d'avoir un
éclairement comparable à celui de la lampe de 75 W dans les conditions
précédentes.
E = I / h'2 ; h' = (I / E )½ =(400 / 100 )½ =2,0 m.
Citerne de récupération de l'eau de pluie. ( 7 points).
On souhaite mettre en place un système permettant de récupérer et de
stocker l'eau de pluie pour alimenter les WC, la machine à laver et les
systèmes d'arrosage.
Pour cela on désire enterrer une citerne et d'y adjoindre une pompe.
Détermination du volume de la citerne.
La citerne de récupération de l'eau de pluie est dimensionnée selon la
quantité d'eau pouvant être récoltée sur la toiture et selon la
consommation des habitants afin d'avoir un compromis teille/
investissement / rentabilité le plus intéressant possible.
La toiture est constituée de 2 pans identiques de longueur L= 15,0 m largeur l=8,0 m.
Calculer sa surface S.
S = 2 L l = 2*15,0 *8,0 =240 m2.
Dans la région où est construite cette maison, le volume d'eau reçu par les toitures est : P = 1,0 m3 par m2 par an. Le taux de récupération T de l'eau de pluie, qui dépend du type de toit, est de T = 50 %.
Calculer le volume VP d'eau de pluie récoltée en un an ainsi que l'économie réalisée sachant que le coût de l'eau est de C = 3,50 € / m3.
VP = P T S / 100 = 1,0 *0,50 *240 =120 m3.
C = 3,50 *120 = 420 €.
Le besoin annuel pour l'utilisation domestique et le jardin est VB = 80 m3 d'eau de pluie.
Le volume V de la citerne est déterminé par le calcul de la moyenne
entre la quantité récupérée en une année et le besoin annuel On
applique ensuite à cette moyenne le coefficient 0,057 ( ce coefficient
correspond au rapport entre le nombre de jours de réserve et le nombre
de jours dans l'année 21 / 365 ).
Calculer V en m3.
Moyenne : ( VP + VB) /2 = (120 + 80) / 2 = 100 m3.
V = 100*0,057 = 5,7 m3.
Puissance de la pompe immergé dans la citerne.
Masse volumique de l'eau r = 1000 kg m-3 ; g = 10 m s-2 ; pression atmosphérique P0 =1,00 105 Pa.
Théorème de Bernoulli : ½r (v2B-v2A) + pB-pA + rg(zB-zA) = P / qv.
On s'intéresse maintenant à la puissance de la pompe immergée dans la
cuve qui permet d'alimenter en eau le lave-linge situé au premier étage
de la maison.
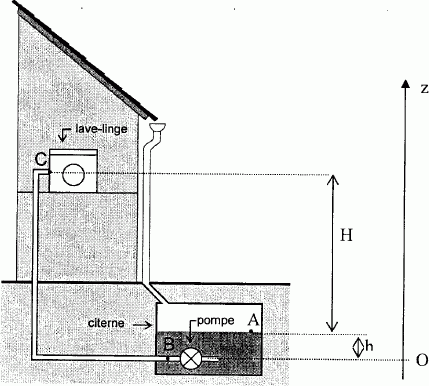
Le lave-linge est mise en
marche et la pompe s'active alors pour remplir son réservoir. On
suppose qu'aux points A et C l'eau est à la pression atmosphérique et
que vA=0.
La vitesse de l'eau dans la canalisation BC, dont la section est S = 2,5 cm2, est v =2,0 m/s.
Lorsque le débit est constant, comment qualifie t-on le régime d'écoulement de l'eau ?
L'écoulement est dit "permanent".
Quel est le débit volumique qv de l'eau dans la canilisation BC ?
qv= S v = 2,5 10-4 *2,0 =5,0 10-4 m3 s-1. ( 0,5 L / s).
En déduire le temps Dt de remplissage du réservoir du lave-linge dont le volume est V = 20 L.
Dt =V / dv =20 / 0,5 = 40 s.
On désire faire monter l'eau d'une hauteur H = 6,0 m au dessus du niveau de la cuve.
En utilisant le théorème de Bernoulli entre A et C, déterminer la puissance P de la pmope immergée.
½r (v2C-v2A) + pC-pA + rg(zC-zA) = P / qv.
zC-zA = H = 6,0 m ; pC = pA ; vA=0 ; vC = v = 2,0 m/s ;
½r v2C + rgH = P / qv ; P =qv r(½ v2C + gH) = 5,0 10-4 *1000 (0,5*4 +10*6,0) =31 W.
Calculer la pression pB au point B, en sortie de pompe sachant que le niveau de la cuve se situe à une hauteur h = 1,0 m au dessus de ce point.
Bernoulli entre les points A et B : ½r (v2B-v2A) + pB-pA + rg(zB-zA) = P / qv.
zB-zA= h = 1,0 m ; pA = 1,0 105 Pa ; vA=0 ; vB = v = 2,0 m/s ;
½r v2B + pB-pA + rgh = P / qv ; pB= pA + P / qv - rgh -½r v2B ;
pB=1,0 105 +31 / 5,0 10-4 -1000*10*1,0 -500*4 =1,5 105 Pa.
|
Combustion dans un poêle à bois.
( 6 points ).
L'utilisation de combustible fossile provoque un accroissement de la concentration en dioxyde de carbone CO2 dans l'atmosphère, qui peut conduire à des changements climatiques ( réchauffement de l'atmosphère ).
La combustion du bois garantit des rejets dans l'atmosphère avec moins
de polluants que la plupart des combustibles fossiles. De plus la
quantité de CO2 dégagé lors de la combustion du bois est
comparable à celle produite naturellement lors de sa décomposition,
cette quantité de CO2 correspond à celle qui a été extraite
par la photosynthèse au cours de la croissance de l'arbre. Un équilibre
est de la sorte obtenu. Le bilan théorique sur le CO2 produit est donc neutre.
A quel phénomène fait-on allusion dans la première partie du texte ?
A l'effet de serre dû à l'augmentation du dioxyde de carbone dans l'atmosphère.
On
chhoisit donc pour cette habitation un chauffage à l'aide d'un poêle à
bois. On s'interesse à la combustion du bois dans ce poêle :
détermination d'un volume de CO2 dégagé ainsi que la possible utilisation des cendres.
Compléter l'équation bilan de la combustion complète de la cellulose.
C6H10O5 + 6O2 =6 CO2 +5 H2O
On souhaite déterminer le volume de CO2 obtenu par
combustion d'une masse m = 1620 g de cellulose contenue dans une bûche.
C : 12,0 ; H : 1,0 ; O : 16,0 g/mol ; volume molaire Vm =32 L/mol
Calculer le nombre de moles n contenues dans m =1620 g de cellulose.
Masse molaire de la cellulose M=6*12+10+5*16 =162 g/mol.
n = m / M = 1620 / 162 = 10 mol.
En déduire le nombre de mole n' de CO2 produites par la combustion.
D'après les coefficients de l'équation : n' = 6 n = 6*10 = 60 mol.
En déduire le volume V de CO2 dégagé.
V = n' Vm = 60*32 =1920 L = 1,92 m3.
A
la fin de la combustion, on peut utiliser les cendres restantes pour le
jardin de l'habitation. En effet les cendres de bois possèdent
certaines propriétés qui peuvent s'avérer utiles pour plusieurs
circonstances en jardinage : la cendre est un alcalinisant ( diminue
l'acidité du sol ), un antiparasitaire et un insectifuge naturel. La
présence de potasse KOH (s) explique son pouvoir alcalinisant.
On dissout des cendres de bois dans de l'eau.
Ecrire l'équation de dissolution de la potasse dans l'eau sachant qu'il se forme des ions potassium K+.
KOH(s) = K+aq + HO-aq.
La solution obtenue a un pH égal à 11.
En déduire la concentration en ion hydroxyde HO-aq.
[HO-aq] = Ke / [H3O+aq] = 10-14 / 10-pH =10-14 / 10-11 =1,0 10-3 mol/L.
Expliquer pourquoi l'épandage de cendres diminuera l'acidité du sol.
L'acidité est due à la présence des ions oxonium H3O+aq.
En présence de cendres, ces derniers réagissent avec les ions hydroxyde HO-aq
H3O+aq + HO-aq = 2H2O(l). |
|
|

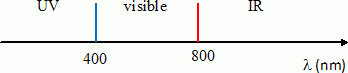
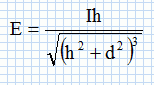 .
.