Réaction de fusion du réacteur ITER.
Le
réacteur ITER en construction à Cadarache doit réaliser une réaction de
fusion nucléaire. Ce réacteur sera alimenté en noyaux de deutérium 21H et en noyaux de lithium baLi.
Le lithium doit fournir des noyaux de tritium 31H, nécessaires à la réaction de fusion. Il se transforme dans le réacteur suivant l'équation :
baLi + 10n --> 42He +31H.
En énonçant les lois utilisées, détermner a et b.
Conservation de la charge : a+0 = 2+1 ; a = 3.
Conservation du nombre de nucléons : b+1 = 4+3 ; b = 6. 63Li.
Qualifier le lien qui relie les noyaux de tritium et de deutérium.
Ce sont des isotopes : même numéro atomique et des nombres de nucléons différents.
La réaction entre les noyaux de deutérium et de tritium doit fournir l'énergie du réacteur, son équation s'écrit :
31H + 21H --> 42He +10n.
Calculer, en unité de masse atomique, la perte de masse Dm qui accompagne cette réaction.
On donne m(31H) = 3,016 u ; m(21H) =2,013 u ; m(42He) = 4,001 u ; m(10n) = 1,009 u.
Dm = m(10n) +m(42He) -m(21H) -m(31H)
Dm =4,001 + 1,009-3,016-2,013 = -1,9 10-2 u.
|
Vérifier que l'énergie E dégagée est 17,7 MeV par noyau de tritium.
On donne 1 u = 931,4 MeV/c2 = 1,66 10-27 kg.
E = 1,9 10-2 *931,4 = 17,7 MeV.
|
La production mondiale annuelle énergétique est actuellement d'environ 12 milliards de TEP.
Quelles sont les masses en tonnes de tritium et de deutérium qu'il faudrait pour produire cette énergie ?
On donne 1 TEP = 4,2 1010 J ; 1 eV = 1,6 10-19 J.
12 milliards TEP = 12 109 * 4,2 1010 =5,04 1020 J.
17,7 MeV = 17,7 106 eV = 17,7 106 *1,6 10-19 =2,832 10-12 J.
Nombre de noyaux de tritium : N = 5,04 1020 / 2,832 10-12 = 1,78 1032 noyaux.
Masse de tritium : 1,78 1032 *3,016 * 1,66 10-27= 8,9 105 kg = 8,9 102 t.
Masse de deutérium : 1,78 1032 *2,013 * 1,66 10-27= 5,95 105 kg =5,9 102 t.
Les réserves mondiales de deutérium dans les océans sont estimées à 4,6 1013 tonnes.
Calculer
le nombre d'années de consommation énergétique mondiale correspondante
dans l'hypothèse que la totalité de la production énergétique est
fournie par des réacteurs à fusion.
4,6 1013 / 5,95 102 = 7,7 1010 années.
En réalité, les réserves de lithium qui sont moins importantes limitent sensiblement cette durée.
L'eau semi-lourde, source de deutérium.
Lorsque deux atomes d'hydrogène de l'eau sont remplacés par deux atomes
de deutérium, on obtient de l'eau lourde. Lorsqu'un seul atome
d'hydrogène de l'eau est remplacé par un atome de deutérium, on parle
d'eau semi-lourde.
Comme l'eau normale, l'eau lourde subit une transformation d'autoprotolyse dont l'équation peut s'écrire :
2H2O = H3O+ + HO-. Ke = [H3O+][HO-] = 1,35 10-15 à 25°C.
Calculer la valeur du pH de l'eau lourde quand il y a autant d'ions H3O+ et HO-.
[H3O+]2 = Ke ; [H3O+] = Ke½ =(1,35 10-15 )½ =3,674 10-8 mol/L
pH = - log [H3O+] = -log 3,674 10-8 = 7,44 ~7,4.
L'enthalpie de formation de l'eau lourde est légèrement différente de celle de l'eau normale et vaut DH°f = -249,20 kJ/mol.
Ecrire et équilibrer l'équation de décomposition de l'eau en dihydrogène et dioxygène.
2H2O = 2H2(g) + O2(g).
Vérifier que l'énergie E nécessaire pour décomposer 1 kg d'eau lourde est de 12,5 MJ.
Masse molaire de l'eau lourde : M = 4+16= 20 g/mol
Quantité de matière d'eau lourde dans m=1000 g : n = m / M = 1000/20 = 50 mol.
E = n |DH°f | =50*249,2 =1,246 104 KJ = 12,46 MJ ~12,5 MJ.
Déterminer en m3 les volumes gazeux formés dans les conditions normales de température et de pression pour 1 kg d'eau lourde.
n(O2) = ½n = 25 mol ; VO2 = n(O2) VM =25*22,4 = 560 L = 0,56 m3.
n(D2) =2n(O2) ; VD2 =2VO2 =1,12 ~1,1 m3.
On suppose que le deutérium présent dans les océans ( 4,6 1013 tonnes) l'est sous forme d'eau semi-lourde.
Calculer la teneur massique en deutérium dans l'eau de mer ( exprimée en g/m3).
On donne le volume des océans : V = 1,4 109 km3 ; masse volumique de l'eau reau = 1000 kg m-3.
4,6 1013 t = 4,6 1019 g ; 1,4 109 km3 = 1,4 1018 m3 ;
Teneur en deutérium : 4,6 1019 / 1,4 1018 = 32,9 ~33 g m-3.
Calculer la concentration en eau semi-lourde dans l'eau de mer ( exprimée en mol m-3).
Masse molaire de l'eau semi-lourde : M = 1+2+16 = 19 g/mol.
32,9 / 19 = 1,7 mol m-3.
Refroidissement d'ITER et alimentation en eau.
Le
réacteur ITER ne produira pas d'électricité. Le but de ce réacteur et
d'étudier et de mettre en oeuvre la réaction de fusion. Un des
objectifs est de pouvoir produire 500 MW de chaleur pendant 400 s.
Afin de dissiper cette chaleur produite, on amène de l'eau qui sera transformée en vapeur.
Quelle est la valeur de l'énergie thermique Q fournie par ITER pendant les 400 s prévues de production ?
énergie (MJ) = puissance (MW) fois durée en seconde.
Q = 500*400 =2,0 105 MJ. ( 2,0 1011 J)
Quelle masse d'eau initialement à 15°C faut-il vaporiser à 100°C pour dissiper cette chaleur ?
On donne Ceau = 4186 J kg-1 K-1 ; Leau = 2 256 kJ kg-1.
Q = m ( Leau + Ceau (100-15)) =m(2,256 106 +4186*85) = 2,612 106 m.
m = Q / 2,612 106 = 2,0 1011 / 2,612 106 =7,657 104 kg = 76,6 t.
Montrer que le débit volumique de l'eau est QV~700 m3 h-1.
76,6 t d'eau soit 76,6 m3sont utilisés en 400 s.
QV = 76,6*3600 / 400 = 689 ~700 m3 h-1.
On
suppose qu'une canalisation droite et horizontale de diamètre D = 500
mm et de longueur L = 1 km est traversée par un débit d'eau QV =700 m3 h-1.
Calculer la vitesse moyenne d'écoulement de cette eau en m/s.
Débit volimique (m3 s-1) = vitesse (m s-1) fois section (m2).
700 m3 h-1 = 700 / 3600 =0,1944 m3s-1. S = p D2/4 = 3,14 *0,52/4 =0,19625 m2.
v = 0,1944 / 0,19625 =0,99 m s-1.
Quel est le nombre de Reynolds Re associé à cet écoulement ?
On donne heau = 1,0 103 Pa s. Re = (r v D) / h.
Re = 1000*0,99*0,500 / 1000 =0,495 ~0,50.
L'écoulement est-il laminaire ou turbulent ? Justifier.
Re est très faible, l'écoulement est laminaire réversible.
Calculer la perte de charge J de la canalisation à l'aide de la formule ci-dessous.
J = 1,1 10-3 QV2 D-5 L = 1,1 10-3 * 0,19442 *0,5-5*1000 =1,33 m.
Montrer que la différence de pression entre les extrémités de la canalisation est 133 hPa si le régime est paermanent.
DP = J g reau =1,33 *10*1000 = 1,33 104 Pa = 133 hPa.
|
Production d'électricité.
Pour
produire de l'électricité il faut une source de chaleur stable. Le
réacteur DEMO qui succédera à ITER devra fournir de façon continue une
puissance thermique de 2 GW par fusion nucléaire.
Le rendement de la conversion de l'énergie thermique en énergie électrique est de 30 %.
En déduire la puissance électrique Pélec du réacteur DEMO.
Pélec =puissance thermique fois le rendement = 2 *0,30 = 0,60 GW.
La chaleur produite par un réacteur peut être transformée en
électricité par l'intermédiaire d'un circuit d'eau / vapeur. Le cycle
suivi par l'eau est schématisé ci-dessous :
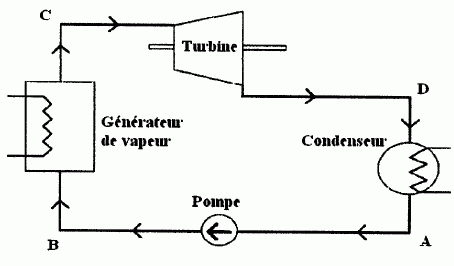
En C, l'eau est sous forme de vapeur sèche à 300°C et 80 bars. Elle subit une détente isentropique dans la turbine.
En D, l'eau est sous forme de vapeur et d'eau liquide à 0,042 bar. Elle
subit une condensation complète isobare dans le condenseur.
En A, l'eau sort sous forme de liquide saturant à 30°C. Elle subit une
compression isentropique dans la pompe sans changement significatif de
température.
En B, l'eau est sous forme liquide à 80 bar. Elle subit un
réchauffement et une vaporisation complète dans le générateur de vapeur.
Quelle est la valeur SD de l'entropie massique du point D ?
On donne : s(C) = 5,8 kJ kg-1 K-1 ; s(A) = 0,4 kJ kg-1 K-1.
G : point de vapeur saturante à 30 °C : s(G) = 8,5 kJ kg-1K-1 ;
La détente CD est isentropique. s(C) =s(D)= 5,8 kJ kg-1 K-1.
Donner l'expression du titre massique en vapeur xM en un point M quelconque du cycle en fonction des entropies massiques sG ( vapeur saturante) sL ( liquide saturant) et SM.
xM = (SM-SL) / (SG-SL).
Vérifier que le titre massique en vapeur xD au point D est environ 67 %.
xD= (SD-SL) / (SG-SL)=(5,8-0,4) / (8,5-0,4) = 5,4 / 8,1 =0,667 (~67 %)
Montrer que la valeur hD de l'enthalpie massique au point D est environ 1750 kJ kg-1.
On donne : h(C) =2786 kJ kg-1. h(G) =2555 kJ kg-1. h(A) =125 kJ kg-1. h(B) =132 kJ kg-1.
Au poin D : titre massique en vapeur 0,667 ; titre massique en liquide : 0,333.
hD = 0,667 h(G) + 0,333 h(A) = 0,667*2555 + 0,333*125 =1745 kJ kg-1.
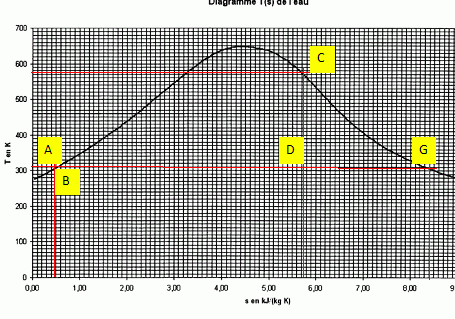
Placer les points A, B, C, D et G surle diagramme T(S) de l'eau.
On souhaite calculer le rendement thèorique du cycle.
Calculer la valeur du travail massique avec transvasement W fournit par la turbine.
W= hD-hC =1750-2786 = -1036 ~-1,0 103 kJ kg-1.
Calculer la valeur de la chaleur massique q consommée par le cycle dans le générateur de vapeur.
q= hC-hB =2786-132 = 2654 ~2,7 103 kJ kg-1.
Déduire des résultats précédents le rendement théorique du cycle.
rendement = |W| / q = 1036/2654 =0,39 (39 %).
|
|
|
|

