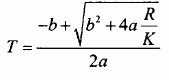Généralités.
Le
document suivant présente la chaîne de mesure simplifiée d'un
spectrophotomètre en figurant par un rectangle chacun des principaux
composants de l'appareil.
Compléter ce schéma.

Dans quel domaines de longueurs d'onde utilise t-on un spectrophotomètre ?
Un soluté coloré absorbe dans le domaine visible ( 400 ; 800 nm ).
Certaines solutions absorbent dans l'ultraviolet ( longueur d'onde
inférieures à 380 nm). L'infrarouge n'est pas utilisé.
A quel domaine correspond le choix d'une lampe à incandescence comme source de lumière ?
Au domaine visible.
Etude de la lampe à incandescence.
Relation température - résistance du filament.
|
On
se propose d'utiliser un modèle expérimental de la variation de la
résistance d'un filament d'ampoule électrique en tungstène en fonction
de sa température. Des mesures expérimentales de la variation de la
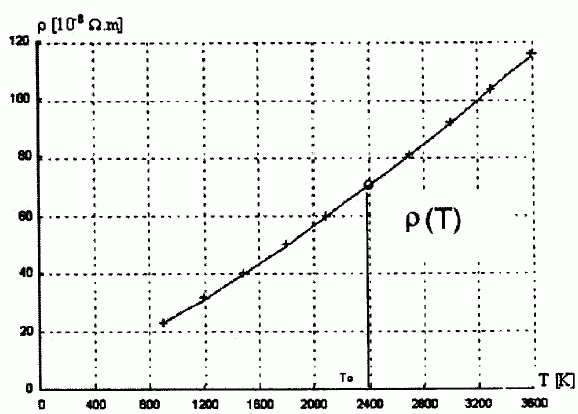
résistivité r du tungstène ont été faites par Jones et Langmuir
|
Ce graphe peut être modélisé par la fonction r = aT2+bT.
a = 2,54 10-14 SI ; b = 2,30 10-10 SI.
Calculer la résistivité r à 300 K et à 2400 K. Par quel facteur est multipliée cette résistivité entre ces deux températures ?
r(300) = 2,54 10-14 *3002 +2,30 10-10 *300 =2,286 10-9 +6,90 10-8 =7,1286 10-8 ~7,13 10-8 W m.
r(2400) = 2,54 10-14 *24002 +2,30 10-10 *2400 =1,463 10-7 +5,52 10-7 =6,983 10-7 ~6,98 10-7 W m.
r(2400) / r(300) =6,983 10-7 / 7,1286 10-8 ~9,80.
La
résistivité est une grandeur intrinsèque du matériau utilisé, alors que
la résistance dépend aussi de sa géométrie. On rappelle que pour un
conducteur cylindrique de section S et de longueur L, la résistance R
se calcule par la relation : R = r L / S. L'intérêt d'utiliser R plutôt que r réside dans la facilité de mesure.
Le fabricant d'ampoule électrique prévoit une température du
filament de 2400 K dans les conditions normales de fonctionnement ( à
savoir 6,0 V et 0,55 A en continu ). Le rayon du filament est r = 0,03
mm.
Déterminer R et en déduire sa longueur L.
R = U / I = 6,0 / 0,55 =10,91 ~11 W.
L = R S / r avec S = 3,14 (0,03 10-3)2 = 2,827 10-9 m2.
L = 10,91 *2,827 10-9 / 6,983 10-7 =4,417 10-2 ~4,4 10-2 m ~4,4 cm.
A partir du modèle choisi pour r(T), montrer que la température T du filament peut s'exprimer sous la forme : 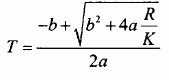
K est une constante égale à R(T0) / r(T0). On supposera que les dimensions du filament sont invariables.
R = (a T2+bT) L / S ; a T2+bT-RS /L = 0
Discriminant : D =b2 +4aRS/L, positif
Seule la solution positive est à retenir : T = [-b + (b2 +4aRS/L)½] / (2a).
Comment procéder pour connaître la température du filament ?
Mesurer la résistance du filament R ; l'expression précédente permet de trouver la température T.
Relation température- couleur du filament.
Dans
le cas de la lampe électrique, l'échauffement est provoqué par les
nombreuses collisions entre les électrons de conduction ety les atomes
du métal constituant le filament. Celui-ci va alors perdre une partie
de cette énergie sous forme de rayonnement électromagnétique
polychromatique, dont la répartition spectrale est fonction de la
température. Ce phénomène est valable pour tout corps porté à une
certaine température ; on parle du rayonnement du corps noir.
La répartition spectrale ul(l) de l'énergie émise par un corps noir est donnée pour quelques températures.
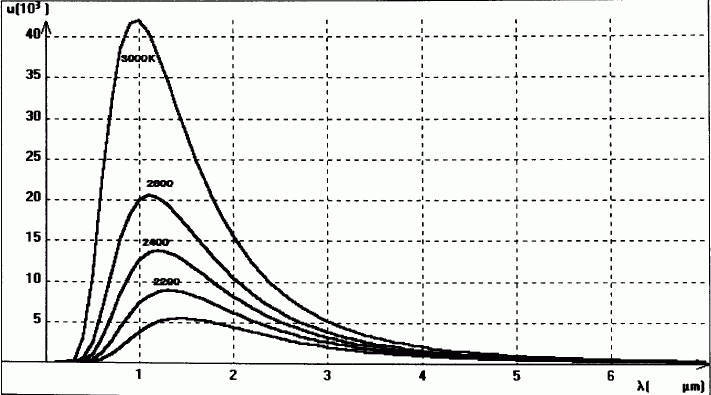
Pour différentes valeurs de T, on obtient des courbes présentant chacune un maximum. La longueur d'onde lM pour laquelle se produit ce maximum est donnée par la loi du déplacement de Wien sous la forme :
lM T = 2898 µm K
Déterminer lM à la température normale de fonctionnement du filament.
lM = 2898 / T = 2898 / 2400 =1,2075 ~1,21 µm.
Dans quel domaine spectral est située cette valeur ?
Cette valeur est supérieure à 0,8 µm : 1,21 µm appartient au domaine infrarouge.
Pourquoi le filament nous semble-t-il cependant blanc ?
La lumière est polychromatique : on y trouve pratiquement toutes les
couleurs de l'arc en ciel. La superposition de toutes ces couleurs
donne l'impression de blanc.
Comparaison avec le soleil.
La température de surface du soleil est 6000 K.
Quelle est la longueur d'onde correspondant au maximum de la répartition spectrale de l'énegie émise ?
lM = 2898 / T = 2898 / 6000 =0,483 µm.
Dans quel domaine spectral est située cette valeur ?
Cette valeur est comprise entre 0,4 µm à 0,8 µm : 0,483 µm appartient au domaine visible.
|
Etude de la photodiode.
Une
photodiode est une diode à jonction P-N dont les caractéristiques
électriques dépendent du flux lumineux reçu par cette jonction. Avec
les conventions d'orientation pour l'intensité I et la tension U
indiquées ci-dessous, l'intensité du courant inverse est fonction de
l'éclairement reçu F et indépendant de la tension U.
Préciser le branchement du voltmètre et de l'ampèremètre sur le montage afin de construire la caractéristique I = f(U).
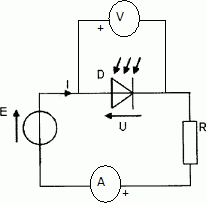
On a relevé la caractéristique.
Indiquer la partie de la caractéristique correspondant au fontionnement en photodiode.
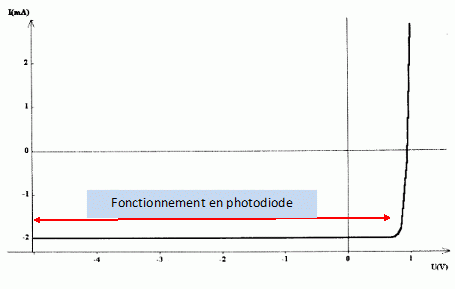
On a mesuré la valeur de l'intensité I du palier pour différentes valeurs de l'élairement F.
Vérifier que les résultats répondent à la relation I=ß F. Préciser la valeur de ß.
F (W m-2)
|
50
|
100
|
150
|
200
|
250
|
I(mA)
|
-0,45
|
-0,90
|
-1,35
|
-1,80
|
-2,25
|
| ß=I / F(mA m2W-1) |
-9 10-3
|
-9 10-3 |
-9 10-3 |
-9 10-3 |
-9 10-3 |
Le rapport I / F est constant : F et I sont proportionnels.
|
|
|