Polarimétrie, produit de solubilité de l'hydroxyde de cuivre (II): BTS biotechnologie 2010.

Le saccharose, le glucose et le fructose sont des substances optiquement actives dont les solutions aqueuses suivent la loi de Biot a = [a]20°CD l Cm. Expliciter les différents termes intervenant dans cette loi. Préciser les unités de chacun des termes. Loi de Biot traduit la proportionnalité entre le pouvoir rotatoire d'un milieu et les concentrations en produits optiquement actifs (dextrogyres ou lévogyres) : a (°) angle de rotation du plan de vibration des ondes lumineuses ; [a] : pouvoir rotatoire spécifique ( ° m2 kg-1 ); Cm: concentration ( kg m-3 ) ; l : longueur (m) de cuve. Ou encore : pouvoir rotatoire spécifique ( °  mL g-1 dm-1 ); Cm: concentration ( g mL-1 ) ; l : longueur (dm) de cuve. On utilise un polarimètre de Laurent pour déterminer le pouvoir rotatoire spécifique du fructose. Des solutions de différentes concentrations sont introduites dans un tube polarimétrique de longueur l = 20,0 cm. Des solutions de différentes concentrations sont introduites dans le tube polarimétrique. On mesure leur pouvoir rotaroire à 20°C pour la raie D du sodium et on obtient le tableau suivant : Cm(g/L) 0 20,0 40,0 60,0 80,0 100 a ( °) 0 -3,70 -7,40 -11,1 -14,7 -18,5 La source lumineuse utilisée est une lampe à vapeur de sodium. Justifier ce choix. Le pouvoir rotatoire spécifique est défini à température donnée et à une longueur d'onde donnée. La raie D du soduim est une lumière quasi-monochromatique. Montrer graphiquement que ces solutions vérifient la loi de Biot. 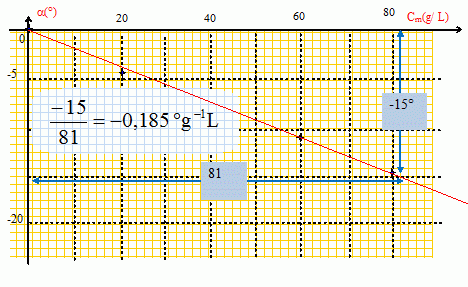La courbe est une droite passant par l'origine de coefficient directeur -0,185 ° L g-1. La loi de Biot est donc vérifiée.   Déduire de la courbe le pouvoir spécifique du fructose. a = [a]20°CD l Cm. Le coefficient directeur vaut : [a]20°CD l = -0,185 ° L g-1 avec l = 2,00 dm. [a]20°CD  =-0,185 / 2 = -0,0925 ° L g-1 dm-1 = -92,5 °  mL g-1 dm-1. Le fructose est-il dextrogyre ou lévogyre ? Justifier. Il existe deux variétés de substances optiquement actives : les substances lévogyres qui font tourner le plan de polarisation vers la gauche et les substances dextrogyres qui font tourner ce plan vers la droite. Par convention, une molécule lévogyre est notée (-), et une molécule dextrogyre est notée (+) : le fructose est lévogyre. On considère un volume V = 1,00 L de solution aqueuse S0 contenant un mélange de glucose et de saccharose de concentrations massiques respectives  C0G =40,1 g/L et C0s =80,3 g/L. Longueur du tube l = 20,0 cm. Pouvoir rotatoire spécifique du glucose : [aG]20°CD =0,527 ° m2 kg-1 ; pouvoir rotatoire spécifique du saccharose : [aS]20°CD =0,665 ° m2 kg-1 ; pouvoir rotatoire spécifique du fructose : [aF]20°CD =-0,920 ° m2 kg-1. Masse molaire du saccharose MS = 342 g/mol ; masse molaire du glucose MG = 180 g/mol ; masse molaire du fructose MF = 180 g/mol. On mesure dans un premier temps le pouvoir rotatoire a0 de la solution S0 à 20 °C. Donner l'expression littérale de a0 puis le calculer. a0  =( [aG]20°CD C0G + [aS]20°CD C0s ) l avec C0G =40,1 kg m-3 et C0s =80,3 kg m-3et l = 0,200 m. a0  =( 0,527*40,1 +0,665*80,3) *0,200 =14,9 °. Dans un deuxième temps, on réalise l'hydrolyse totale du saccharose dans le mélange selon l'équation de la réaction chimique suivante pour obtenir une solution finale Sf. C12H22011 (saccharose )+ H20 ---> C6H1206 (glucose ) + C6H1206 (fructose ). Montrer que les quantités de matière initiales en saccharose n0S et en glucose n0G valent respectivement dans la solution S0, 0 235 mol et 0,223 mol. n0S =  C0s V / MS= 80,3 *1 / 342 =0,235 mol. n0G =  C0G V / MG= 40,1 *1 / 180 =0,223 mol. Compléter le tableau d'avancement de cette réaction totale. équation de la réaction C12H22011 +H20 ---> C6H1206(glucose ) + C6H1206 (fructose ) avancement quantités de matière (mol) initial 0 0,235 solvant 0,223 0 final xmax = 0,235 0,235 -xmax = 0 large excès 0,223 + xmax =0,223+0,235 =0,458 xmax = 0,235 En considèrant que l'hydrolyse se fait sans variation de volume, déterminer les concentrations massiques CfG en glucose et CfF en fructose dans la solution Sf. CfG =0,458*180 = 82,44 g /L~82,4 g/L et CfF =0,235*180 = 42,3 g /L. Donner l'expression littérale du pouvoir rotatoire af puis le calculer. a0  =( [aG]20°CD CfG + [aF]20°CD CfF ) l avec CfG =82,4 kg m-3 et CfF =42,3 kg m-3et l = 0,200 m. a0  =( 0,527*82,4 -0,92*42,3) *0,200 =0,902 °. Produit de solubilité. L'hydroxyde de cuivre (II) Cu(OH)2 (s) est utilisé entre autres por protéger la vigne contre le mildiou. C'est un sel très peu soluble dans l'eau. On se propose de déterminer le produit de solubilité de l'hydroxyde de cuivre (II) de différentes façons. On donne : E°(Cu2+aq / Cu(s) = 0,337 V. Conductivité équivalente limite ( unité SI) lCu2+aq = 5,35 10-3 ; lHO-aq = 19,95 10-3 . La dissociation de l'eau sera considérée comme négligeable. La solubilité de l'hydroxyde de cuivre (II) dans l'eau pure à 25°C a pour valeur s = 4,0 10-7 mol/L. Ecrire l'équation de dissolution de l'hydroxyde de cuivre (II) dans  l'eau pure. Cu(OH)2 (s) = Cu2+aq + 2HO-aq. Exprimer le produit de solubilité Ks en fonction des concentrations molaires des espèces présentes en solution. Ks = [Cu2+aq] [HO-aq]2. Etablir l'expression littérale de Ks en fonction de la solubilité s. Calculer sa valeur. s = [Cu2+aq] ; la solution est électriquement neutre : [HO-aq] = 2[Cu2+aq] = 2 s ; Ks = s (2s)2 = 4 s3 = 4 (4,0 10-7 )3 = 2,56 10-19 ~2,6 10-19. Le pH d'une solution aqueuse saturée d'hydroxyde de cuivre (II) est égal à 7,9 à 25°C. Déterminer la concentration molaire des espèces présentes en solution. [H3O+aq] = 10-pH = 10-7,9 =1,26 10-8 ~1,3 10-8 mo/L. [HO-aq] = 10-14 / [H3O+aq] = 10-14 / 1,26 10-8 =7,94 10-7 ~ 7,9 10-7 mol/L. La solution est électriquement neutre : 2[Cu2+aq] +[H3O+aq]= [HO-aq] [Cu2+aq] =½( [HO-aq] -[H3O+aq] ) =0,5 ( 7,94 10-7  -1,26 10-8 ) =3,91 10-7 ~3,9 10-7 mol/L. En déduire Ks. Ks = [Cu2+aq] [HO-aq]2= 3,91 10-7 *(7,94 10-7)2 =2,46 10-19 ~2,5 10-19. La conductivité d'une solution ionique est donnée par la relation : s = S Li |zi| Ci. Préciser la signification de chaque terme et les unités SI correspondantes. s  : conductivité S m-1 ; Li : conductivité molaire limite en S m2 mol-1 ; zi : valeur absolue de la charge de l'ion ; Ci : concentration en mol m-3. La conductivité d'une solution aqueuse saturée d'hydroxyde de cuivre (II), mesurée à 25 °C, a pour valeur 2,0 10-5 S m-1.  Calculer les concentrations molaires en ion cuivre (II) et en ion hydroxyde. L'ion oxonium est négligeable à pH= 7,9. La solution est électriquement neutre : [HO-aq] = 2[Cu2+aq]. s  = 2LCu2+aq [Cu2+aq] +LHO-aq [HO-aq] = (LCu2+aq +LHO-aq) [HO-aq] [HO-aq] =2,0 10-5 /( 5,35 10-3+19,95 10-3 ) = 7,9 10-4 mol m-3 = 7,9 10-7 mol / L. [Cu2+aq]=½[HO-aq]  =0,5*7,9 10-7 =3,953 10-7~4,0 10-7 mol / L. En déduire Ks. Ks = [Cu2+aq] [HO-aq]2= 3,953 10-7 *(7,90 10-7)2 =2,47 10-19 ~2,5 10-19. Le potentiel redox d'une électrode constituée d'une lame de cuivre plongeant dans une solution aqueuse saturée d'hydroxyde de cuivre (II) est égal à 0,145 V à 25°C. Exprimer ce potentiel en fonction de [Cu2+aq]. En déduire Ks. Cu2+aq + 2e- = Cu(s) ; E1 = E°1 (Cu2+aq / Cu(s)) + 0,03 log [Cu2+aq] = 0,337+0,03 log [Cu2+aq]= 0,145 V. 0,03 log [Cu2+aq]= 0,145-0,337 =-0,192 ; log [Cu2+aq] =-0,192 / 0,03 = -6,4 ; [Cu2+aq] = 10-6,4 =3,98 10-7 mol/L. La solution est électriquement neutre : [HO-aq] = 2[Cu2+aq] = 7,96 10-7 mol/L. Ks = [Cu2+aq] [HO-aq]2= 3,98 10-7 *(7,96 10-7)2 =2,52 10-19 ~2,5 10-19. Les valeurs trouvées pour Ks sont compatibles entre elles. Ecart relatif = 100 (plus grande valeur - plus petite valeur ) / valeur moyenne = 100 ( 2,52-2,47) / 2,5 = 2 %. Expliquer qualitativement pourquoi l'hydroxyde de cuivre est très peu soluble dans l'eau. Le produit de solubilité est très faible.

menu