|
|
Spectroscopie de l'atome de lithium. (15 points)
Le spectre d'un atome peut être considéré comme sa carte d'identité ;
il permet de connaître des informations telles que les différents
niveaux d'énergie atomiques.
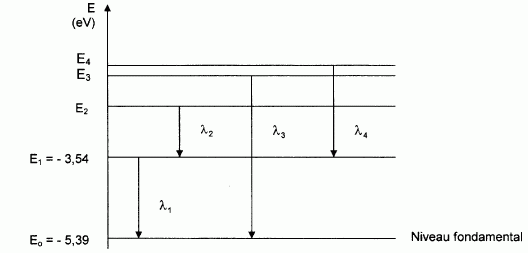
La figure ci-dessous représente le diagramme très simplifié des niveaux
d'énergie de l'atome de lithium Li et quatre transitions entre ces
niveaux.
On donne : c = 3,00 108 m/s ; h = 6,63 10-34 Js ; 1 eV = 1,60 10-19 J.
Les longueurs d'onde associées à ces transitions sont : l1 ; l2=812 nm ; l3 = 323 nm ; l4 =610 nm.
A quels domaines de radiations correspondent les longueurs d'ondes l2 ; l3 ; l4 .
Les longueurs d'onde du domaine visible s'étendent de 400 nm à 800 nm.
l2 : IR ; l3 : UV ; l4 = visible.
Ces quatre radiations correspondent-elles à l'absorption ou à l'émission de photons ? Justifier.
L'atome de lithium revient à un niveau de moindre énergie en
libérant son " surplus " d'énergie sous forme de photon : donc spectre
d'émission.
Calculer en eV les énergies W1, W2, W3, W4 des photons correspondants.
W1 = E1-E0 =-3,54-(-5,39) =1,85 eV.
W2 =hc / l2= 6,63 10-34 *3,00 108 / 812 10-9 =2,45 10-19 J
2,45 10-19 /1,60 10-19 = 1,53 eV.
W3 =hc / l3= 6,63 10-34 *3,00 108 / 323 10-9 =6,16 10-19 J
6,16 10-19 /1,60 10-19 = 3,85 eV.
W4 =hc / l4= 6,63 10-34 *3,00 108 / 610 10-9 =3,26 10-19 J
3,26 10-19 /1,60 10-19 = 2,04 eV.
|
|
En déduire les énergies E2, E3, E4.
W2 = |E1-E2| ; E2 = W2+E1 =1,53-3,54= -2,01 eV.
W3 = |E0-E3| ; E3 = W3+E0 =3,85-5,39= -1,54 eV.
W4 = |E1-E4| ; E4 = W4+E1 =2,04-3,54= -1,50 eV.
|
Un photon d'énergie W = 3,00 eV peut-il être absorbé par l'atome de lithium pris dans son état fondamental ?
Hypothèse : le photon est absorbé :
l'énergie de l'atome devient : -5,39 +3,00 = -2,39 eV.
Or -2,39 eV ne correspond ni à E2, ni à E3, ni à E4.
Les énergies de l'atome sont quantifiées : -2,39 eV est une valeur "interdite".
Le photon d'énergie 3,00 eV ne peut donc pas être absorbé par l'atome de lithium pris dans son état fondamental.
Déterminer l'énergie d'ionisation de l'atome de lithium pris dans son état fondamental.
L'énergie d'ionisation est l'énergie qu'il faut fournir pour arracher
un électron en partant de l'état fondamental : 5,39 eV.
Un photon d'énergie 6,00 eV peut-il ioniser l'atome de lithium pris dans son état fondamental ?
Si oui, quelle est l'énergie cinétique de l'électron éjecté ?
L'énergie
du photon est supérieure à l'énergie d'ionisation : ce photon ionise
l'atome et le "surplus" d'énergie est emporté par l'électron sous forme
cinétique.
Energie cintétique de l'électron : 6,00-5,39 = 0,61 eV.
Quel appareil permet d'observer la partie visible du spectre d'une lampe à vapeur de sodium ?
Spectroscope utilisant un réseau.
Microscope. (15 points)
Inventé au XVIIème siècle, le microscope est un système optique très répandu dans les laboratoires.
Le modèle utilisé par un expérimentateur est constitué d'un objectif et
d'un oculaire assimilés à des lentilles minces, respectivement L1 et L2, de centres optiques O1 et O2.
Les distances focales de l'objectif et de l'oculaire sont respectivement : f'1 = 4,00 mm et f'2 = 4,00 cm.
L'intervalle optique entre les deux lentilles, noté D, est la distance qui sépare le foyer image F'1 de l'objectif du foyer objet F2 de l'oculaire. D =16,0 cm.
Un expérimentateur ayant une vue normale ( vision distincte entre l'infini et la distance minimale de vision distincte dm=25,0
cm ) observe à travers le microscope l'image finale A'B'
perpendiculaire à l'axe optique donnée par l'instrument d'optique d'un
objet AB. Ce dernier de longueur 2,0µm est placé perpendiculairement à
l'axe optique à 4,10 mm devant l'objectif. ( le pied A de l'objet
et le pied A' de l'image sont situés sur l'axe optique).
Vision sans accommodation.
Démontrer par le calcul que l'image intermédiaire A1B1 est dans le plan focal objet de l'oculaire.
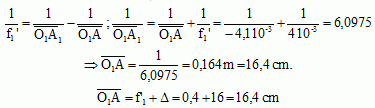
Déterminer sa taille.
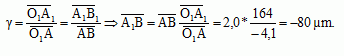
La taille de l'image intermédiaire est 80 µm.
Citer trois caractéristiques de l'image intermédiaire.
L'image est réelle, inversée par rapport à l'objet, plus grande que l'objet.
Déterminer sans calcul la position de l'image finale A'B'.
A1B1 joue le rôle d'objet pour l'oculaire ; cet objet est dans le plan focal objet de l'oculaire : l'image A'B' est à l'infini.
Faire un schéma clair du microscope sans échelle en faisant apparaître les images A1B1 et A'B'.
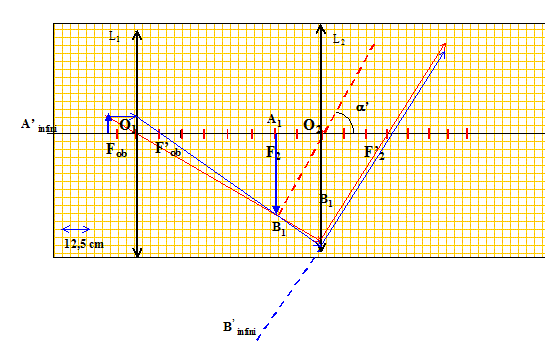
|
|
Calculs de quatre grandeurs caractéristiques du microscope
Définir les grandeurs Pi et Gc et calculer leurs valeurs.
On donne : Pi = D / (f'1x f'2) ; Gc = Pi x dm.
Pi : puissance intrinsèque
La puissance du microscope est P=a'/AB ; dans le cas d'une observation à l'infini, P est la puissance intrinsèque.
Pi = 0,16 / ( 4,0 10-3 x 4,0 10-2) =1000 d.
Gc = 1000*0,25 = 250.
Deux nombres sont gravés sur l'objectif, dont l'un est l'ouverture numérique.
Indiquer à quelle grandeur correspond l'autre nombre. Déterminer sa valeur.
Le grandissement (ou grossissemnt) latéral ( ou transversal) de l'objectif :
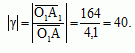
Un seul nombre est gravé sur l'oculaire.
Indiquer à quelle grandeur correspond l'autre nombre. Déterminer sa valeur.
Grossissement commercial de l'oculaire.
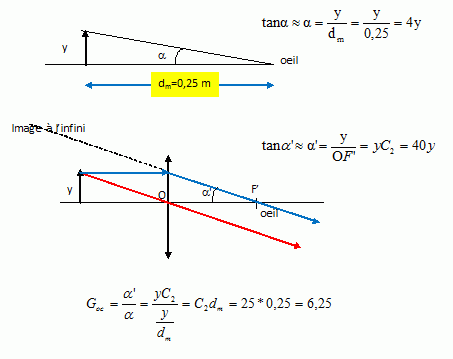
On démontre que pour un objectif de 6,00 mm de diamètre, son image
donnée par l'oculaire est à 4,98 cm du centre optique de l'oculaire et
possède un diamètre de 1,5 mm environ.
Indiquer le nom usuel donné à cette image de lobjectif par l'oculaire.
Le cercle oculaire.
L'expérimentateur se place environ à 5 cm de l'oculaire. La pupille dilatée de l'oeil a un diamètre approximatif de 8 mm.
Justifier le fait que l'observation soit effectuée dans les conditions optimales de luminosité.
Le cercle oculaire ( C'D' figure ci-dessous) d'un
instrument d'optique est l'image de l'objectif à
travers l'oculaire.
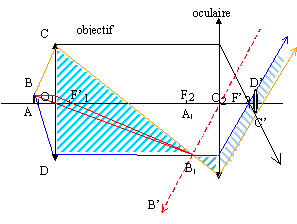
Tous les rayons qui entrent dans le microscope par
l'objectif sortent donc par le cercle oculaire.
On doit placer la pupille de l'œil dans ce cercle
afin qu'un maximum de lumière entre dans le
récepteur, l'oeil.
|
.
|
|