Dosage  ; spectroscopie : Bts analyses de biologie médicale 2009

Spectroscopie UV-visible. Définir la transmmittance d'un milieu absorbant et donner la relation liant l'absorbance A et la transmittance T. Lorsqu'une lumière monochromatique d'intensité I0 traverse un milieu homogène, l'intensité de la lumière émergente I décroît exponentiellement lorsque l'épaisseur l du milieu absorbant augmente. I = I0 . e (- al) a est une constante appelée coefficient d'absorption, caractéristique du milieu et de la longueur d'onde considérés. Dans le cas des solutions, la loi de Beer fait intervenir les concentrations. I = I0 . e (- elc) où e est un coefficient caractéristique de la substance appelé coefficient d'absorbance (L mol-1 cm-1), l est l'épaisseur de la cuve (cm) et c la concentration de la solution (mol/L). Cette loi est vérifiée lorsque la solution est de concentration inférieure à : c < 0,1 mol.L-1. La relation fondamentale utilisée en spectrophotométrie est présentée sous la forme : A= log (I0/I) = elc ( A est l'absorbance ou densité optique) e est une caractéristique de la molécule. Plus e sera grand, plus la solution absorbe. Absorbance et concentration étant proportionnelles, cette relation peut être utilisée pour réaliser des dosages ou des suivis cinétiques. La transmission T est définie comme le rapport de l'intensité transmise à l'intensité incidente. T = I / I0 ; log T= -A. 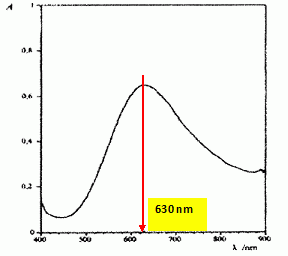Le spectre d'absorption du complexe Cu(NH3)42+ est donné ci-dessous. Comment choisir la longueur d'onde de travail ? Justifier. Pour une meilleur sensibilité, la longueur d'onde de travail  correspond au maximum d'absorption.   Le diagramme énergétique d'une molécule est très complexe et lors de l'absorption d'un photon, il peut se produire une transition entre : - niveaux électroniques si  l'énergie du photon mis en jeu est de l'ordre de quelques électrons volts - niveaux vibrationnels si  l'énergie du photon mis en jeu est de l'ordre de quelques dixièmes d'électrons volts. Calculer l'énergie du photon mis en jeu à 630 nm et conclure sur la nature des transitions mises en jeu en spectroscopie UV visible. On donne : constante de Plank h = 6,63 10-34 Js ; c = 3,00 108 m/s et 1 eV = 1,60 10-19 J. E = h c / l = 6,63 10-34 * 3,00 108 /630 10-9 =3,157 10-19 ~3,16 10-19 J. 3,157 10-19 / 1,60 10-19 =1,97 eV. La  transition se produit entre deux niveaux électroniques. Courbes d'étalonnage. A partir d'une solution mère, on réalise différentes  solutions de concentrations C différentes en l'espèce Cu(NH3)42+et on mesure leur absorbance A dans une cuve d'épaisseur 1,0 cm à la longueur d'onde de travail. On trace la courbe A = f(C). La loi de Lambert est-elle vérifiée ? Justifier. 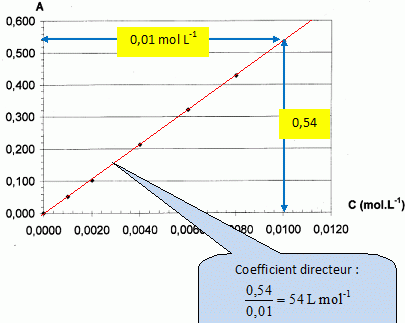L'absorbance et la concentration étant proportionnelles ( le graphe est une droite), la loi de Beer est vérifiée. A la longueur d'onde de travail, calculer le coefficient d'extinction molaire. A = e C l ; le coefficient directeur de la droite est 54 L mol-1 ; d'où e l = 54 et  e = 54 / 1 =  54 L mol-1 cm-1.     Dosage d'une solution de concentration inconnue. On désire connaître la concentration Cinc d'une solution S0 de sulfate de cuivre Cu2+aq + SO42-aq. Dans une fiole jaugée de 100,0 mL, on introduit 50,0 mL de la solution de concentration inconnue auquels on ajoute 2,80 10-2 mol d'ammoniac NH3 et enfin 3,80 10-2 mol de nitrate d'ammonium. NH4NO3 solide. Après dissolution du solide on complète  avec de l'eau distillée jusqu'au trait de jauge et on homogénéise. La solution obtenue est appelée S1. On mesure son absorbance  à la longueur d'onde de travail ; celle-ci vaut 0,270. Déterminer graphiquement la concentration de la solution S1. 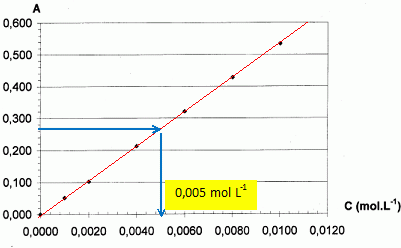CS1 = 5,0 10-3 mol L-1. En déduire Cinc de la solution S0. Le facteur de dilution vaut F = 100 / 50 = 2 d'où Cinc = 2 x CS1 = 1,0 10-2 mol L-1. Préparation de la solution mère. On confectionne une solution aqueuse dans de nouvelles conditions de travail. Dans une fiole jaugée de 1,00 L, on introduit  500 mL de sulfate de cuivre de concentration connue 2,00 10-2 mol/L auxquels on ajoute 0,280 mol d'ammoniac et enfin 0,380 mol de nitrate d'ammonium solide. Après dissolution du solide, on complète avec de l'eau distillée jusqu'au trait de jauge et on homogénéise. La solution obtenue est appelée solution mère. Rôle de l'ammoniac. Les ions Cu2+aq  donnent lieu  à la formation d'ions complexe avec de nombreux ligands comme l'eau, l'ammoniac ou encore les ions chlorure. Quelle propriété commune possèdent ces espèces leur permettant de jouer le rôle de ligands ? L'ion Cu2+ est  un acide de Lewis ( accepteur d'électrons) ; les ligands comme l'eau, l'ammoniac ou encore les ions chlorure sont des bases de Lewis ( donneur d'électrons ). La liaison formée ( liaison covalente de coordination ) résulte du don de deux électrons par le ligand. Ecrire l'équation bilan de la formation du complexe Cu(NH3)42+ à partir des ions cuivre et de l'ammoniac. Cu2+ + 4 NH3 = Cu(NH3)42+. En faisant l'hypothèse que la seule réaction ayant lieu lors de la préparation de la solution mère est celle de la formation du complexe et que cette réaction est pratiquement totale. Déterminer  à l'équilibre, les concentrations [Cu(NH3)42+] et [NH3]. On donne pKd(Cu(NH3)42+) = 12,6 à 25°C. avancement volumique ( mol/L) Cu2+ + 4 NH3 = Cu(NH3)42+ état initial 0 1,00 10-2 0,280 0 état intermédiaire x 1,00 10-2 -x 0,280-4x x à l'équilibre xéq 1,00 10-2 -xéq 0,280-4xéq xéq La réaction étant totale xéq est voisin de xmax : Si  Cu2+est  en défaut : 1,00 10-2 -xéq = 0 soit xéq = 1,00 10-2 mol/L. Si   NH3 est en défaut :  0,280-4xéq=0 soit xéq = 7,00 10-2 mol/L. On retient la plus petite valeur : xéq ~1,00 10-2 mol/L. Par suite : [Cu(NH3)42+] ~1,00 10-2 mol/L ; [NH3] = 0,280-4*1,00 10-2 =0,240 mol/L. Montrer que l'on a [Cu2+] = 7,57 10-13 mol/L. Kd =10-12,6 ; Constante de formation du complexe : Kf = 1012,6 = 3,98 1012. Kf =[Cu(NH3)42+] / ( [Cu2+] [NH3]4 )  ; [Cu2+] = [Cu(NH3)42+] / ( Kf [NH3]4 ) [Cu2+] = 1,00 10-2 / ( 3,98 1012 * 0,2404) = 7,57 10-13 mol/L.   Rôle du nitrate d'ammonium. En milieu très basique on observe la précipitation  de l'hydroxyde de cuivre (II) Cu(OH)2. On montre que la précipitation de Cu(OH)2 dans une solution contenant 7,57 10-13 mol d'ion Cu2+ a lieu lorsque le pH de la solution est supérieur à 10,8 à 25°C. Une solution aqueuse contenant uniquement 0,280 mol d'ammoniac a un pH = 11,3. Dans une telle solution, observerait-on la précipitation de Cu(OH)2 ? Le pH de la solution d'ammoniac est supérieur  à 10,8 : on peut donc observer la précipitation de Cu(OH)2. Calculer le pH d'une solution aqueuse contenant 0,280 mol d'ammoniac et 0,380 mol d'ion ammonium NH4+. On donne pKa(NH4+ / NH3) = 9,2. pH = pKa(NH4+ / NH3) + log [NH4+ ] /[ NH3]) = 9,2 + log 0,380/0,280) = 9,33~9,3. Comment appelle t-on une telle solution ? Le pH étant très proche du pKa(NH4+ / NH3), cette solution est une solution tampon. Dans une telle solution observerait-on la précipitation de Cu(OH)2 ? Le pH de cette solution reste voisin de 9,3, valeur inférieure  à 10,8 : Cu(OH)2 ne précipite pas. Rappeler  les conditions de validité de  la loi de beer-Lambert et justifier la nécessité d'ajouter du nitrate d'ammonium lors de la préparation de la solution mère afin d'éviter la précipitation de Cu(OH)2. La concentration de l'espèce absorbante à la longueur d'onde de travail  doit être inférieure à 0,1 mol/L. Une seule espèce doit absorber à la longueur d'onde de travail. Aucun précipité ne doit se former.   .

retour -menu